Алгоритм Флойда-Уоршелла

Привет, сегодня поговорим про алгоритм флойда - уоршелла, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое алгоритм флойда - уоршелла , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.

алгоритм флойда - уоршелла — динамический алгоритм для нахождения кратчайших расстояний между всеми вершинами взвешенного ориентированного графа. Разработан в 1962 году Робертом Флойдом и Стивеном Уоршеллом.

В информатике алгоритм Флойда–Уоршелла (также известный как алгоритм Флойда, алгоритм Роя–Уоршелла, алгоритм Роя–Флойда или алгоритм WFI) - это алгоритм поиска кратчайших путей во взвешенном графе с положительным или отрицательным весом ребер (но без отрицательных циклов). За одно выполнение алгоритма будут найдены длины (суммарные веса) кратчайших путей между всеми парами вершин. Хотя он не возвращает детали самих путей, можно реконструировать пути с помощью простых модификаций алгоритма. Варианты алгоритма также могут быть использованы для поиска транзитивного замыкания отношения или (в связи с системой голосования Шульце) наиболее широких путей между всеми парами вершин взвешенного графа.

Более строгая формулировка этой задачи следующая:
есть ориентированный граф G = (V, Е) каждой дуге v -> w этого графа сопоставлена неотрицательная стоимость C[v, w]. Общая задача нахождения кратчайших путей заключается в нахождении для каждой упорядоченной пары вершин v, w) любого пути от вершины v в вершины w, длина которого минимальна среди всех возможных путей от v к w.

Формальное описание

Для определенности положим, что вершины графа последовательно пронумерованы от 1 до n. Алгоритм Флойда использует матрицу А размера п * n, в которой вычисляются длины кратчайших путей. Вначале A[i, j] = C[i, j] для всех i != j. Если дуга i -» j отсутствует, то C[i, j] = infinity. Каждый диагональный элемент матрицы А равен 0.

Над матрицей А выполняется п итераций. После k-й итерации A[i, j] содержит значение наименьшей длины путей из вершины i в вершину у, которые не проходят через вершины с номером, большим k. Другими словами, между концевыми вершинами пути i и у могут находиться только вершины, номера которых меньше или равны k. На k-й итерации для вычисления матрицы А применяется следующая формула:
A_k[i,j]=min(A_k-1[i,j], A_k-1[i,k]+A_k-1[k,j])

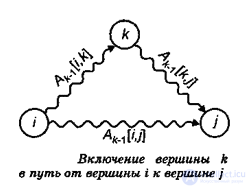
Нижний индекс k обозначает значение матрицы А после k-й итерации, но это не означает, что существует п различных матриц, этот индекс используется для сокращения записи. Для вычисления A_k[i, j] проводится сравнение величины A_k-i[i, j] (т.е. стоимость пути от вершины i к вершине j без участия вершины k или другой вершины с более высоким номером) с величиной A_k-1[i, k] + A_k-1[k, j] (стоимость пути от вершины i до вершины k плюс стоимость пути от вершины k до вершины j). Если путь через вершину k дешевле, чем A_k-1[i, j], то величина A_k[i, j] изменяется.

Наиболее часто используемое название, метод получил в честь двух американских исследователей Роберта Флойда и Стивена Уоршелла, одновременно открывших его в 1962 году. Реже встречаются другие варианты наименований: алгоритм Рой – Уоршелла или алгоритм Рой – Флойда. Рой – фамилия профессора, который разработал аналогичный алгоритм на 3 года раньше коллег (в 1959 г.), но это его открытие осталось безвестным. Алгоритм Флойда – Уоршелла – динамический алгоритм вычисления значений кратчайших путей для каждой из вершин графа. Метод работает на взвешенных графах, с положительными и отрицательными весами ребер, но без отрицательных циклов, являясь, таким образом, более общим в сравнении с алгоритмом Дейкстры, т. к. последний не работает с отрицательными весами ребер, и к тому же классическая его реализация подразумевает определение оптимальных расстояний от одной вершины до всех остальных.

Для реализации алгоритма Флойда – Уоршелла сформируем матрицу смежности D[][] графа G=(V, E), в котором каждая вершина пронумерована от 1 до |V|. Эта матрица имеет размер |V|´|V|, и каждому ее элементу D[i][j] присвоен вес ребра, идущего из вершины i в вершину j. По мере выполнения алгоритма, данная матрица будет перезаписываться: в каждую из ее ячеек внесется значение, определяющее оптимальную длину пути из вершины i в вершину j (отказ от выделения специального массива для этой цели сохранит память и время). Теперь, перед составлением основной части алгоритма, необходимо разобраться с содержанием матрицы кратчайших путей. Поскольку каждый ее элемент D[i][j] должен содержать наименьший из имеющихся маршрутов, то сразу можно сказать, что для единичной вершины он равен нулю, даже если она имеет петлю (отрицательные циклы не рассматриваются), следовательно, все элементы главной диагонали (D[i][i]) нужно обнулить. А чтобы нулевые недиагональные элементы (матрица смежности могла иметь нули в тех местах, где нет непосредственного ребра между вершинами i и j) сменили по возможности свое значение, определим их равными бесконечности, которая в программе может являться, например, максимально возможной длинной пути в графе, либо просто – большим числом.

Ключевая часть алгоритма, состоя из трех циклов, выражения и условного оператора, записывается довольно компактно:

Кратчайший путь из вершины i в вершину j может проходить, как только через них самих, так и через множество других вершин k∈(1, …, |V|). Оптимальным из i в j будет путь или не проходящий через k, или проходящий. Заключить о наличии второго случая, значит установить, что такой путь идет из i до k, а затем из k до j, поэтому должно заменить, значение кратчайшего пути D[i][j] суммой D[i][k]+D[k][j].

Пример

Алгоритм выше выполняется на графе слева внизу:

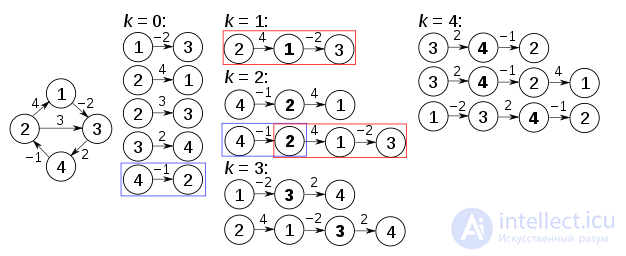
До первой рекурсии внешнего цикла, обозначенного выше k = 0, единственные известные пути соответствуют отдельным ребрам в графе. При k = 1 находятся пути, проходящие через вершину 1: в частности, найден путь [2,1,3], заменяющий путь [2,3], который имеет меньше ребер, но длиннее (с точки зрения веса ). При k = 2 находятся пути, проходящие через вершины 1,2. Красные и синие прямоугольники показывают, как путь [4,2,1,3] собирается из двух известных путей [4,2] и [2,1,3], встреченных в предыдущих итерациях, с 2 на пересечении. Путь [4,2,3] не рассматривается, потому что [2,1,3] - это кратчайший путь, встреченный до сих пор от 2 до 3. При k = 3 пути, проходящие через вершины 1,2,3 найдены. Наконец, при k = 4 находятся все кратчайшие пути.

Матрица расстояний на каждой итерации k, обновленные расстояния выделены жирным шрифтом, будет иметь вид:

Поведение с отрицательными циклами

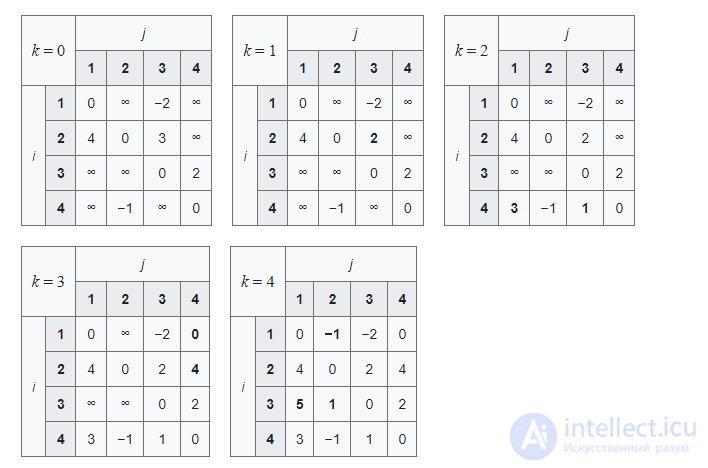
Отрицательный цикл - это цикл, сумма ребер которого равна отрицательному значению. Не существует кратчайшего пути между любой парой вершин , , которые являются частью отрицательного цикла, потому что длина пути от до может быть сколь угодно малой (отрицательный). Об этом говорит сайт https://intellect.icu . Для численно значимого вывода алгоритм Флойда–Уоршелла предполагает отсутствие отрицательных циклов. Тем не менее, если есть отрицательные циклы, алгоритм Флойда–Уоршелла может быть использован для их обнаружения. Очевидно алгоритм заключается в следующем:

• Алгоритм Флойда–Уоршелла итеративно просматривает длину пути

между всеми парами вершин , включая те где ;

• Изначально длина пути равна нулю;
• Путь может улучшиться только в том случае, если его длина

меньше нуля, т.е. обозначает отрицательный цикл;

• Таким образом, после алгоритма, будет отрицательным, если

существует путь отрицательной длины от до .

Следовательно, чтобы обнаружить отрицательные циклы с помощью алгоритма Флойда–Уоршелла, можно проверить диагональ матрицы кратчайших путей, и наличие отрицательного числа указывает на то, что граф содержит по крайней мере один отрицательный цикл. Во время выполнения алгоритма, если есть отрицательный цикл, могут появиться экспоненциально большие числа, вплоть до , где - наибольшее абсолютное значение отрицательного ребра в графе. Чтобы избежать проблем переполнения/потери значимости, следует проверять наличие отрицательных чисел на диагонали матрицы кратчайших путей внутри внутреннего цикла for алгоритма. Очевидно, что в неориентированном графе отрицательное ребро создает отрицательный цикл (то есть замкнутый обход), включающий его инцидентные вершины. Рассматривая все ребра приведенного выше примера графа как неориентированные, например последовательность вершин 4 - 2 - 4 представляет собой цикл с весовой суммой - 2.

примеры реализации

Рассмотрим полный код алгоритма Флойда – Уоршелла на псевддокоде C++ и Паскале, а затем детально разберем последовательность выполняемых им действий.

Псевдокод

Код программы на C++:

Код программы на Pascal:

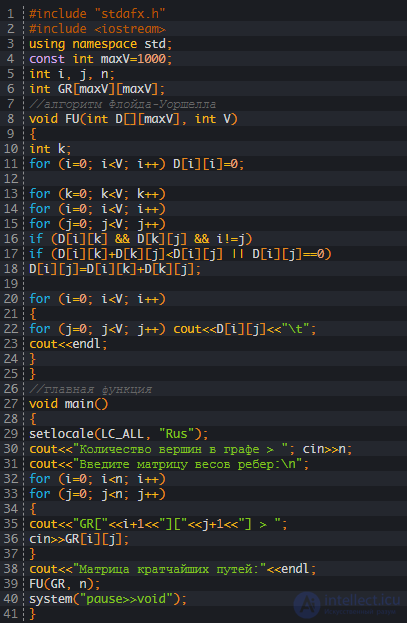
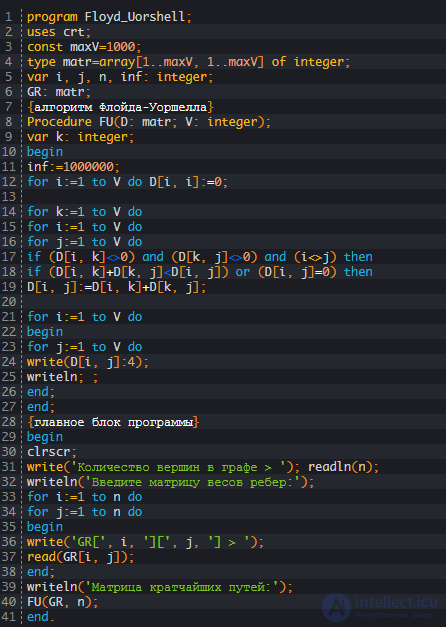
Положим, что в качестве матрицы смежности, каждый элемент которой хранит вес некоторого ребра, была задана следующая матрица:

Количество вершин в графе, представлением которого является данная матрица, равно 3, и, причем между каждыми двумя вершинами существует ребро. Вот собственно сам этот граф:

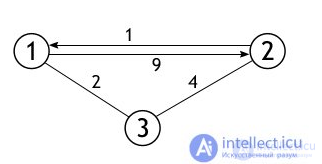
Задача алгоритма: перезаписать данную матрицу так, чтобы каждая ячейка вместо веса ребра из i в j, содержала кратчайший путь из i в j. Для примера взят совсем маленький граф, и поэтому не будет не чего удивительного, если матрица сохранит свое изначальное состояние. Но результат тестирования программы показывает замену двух значений в ней. Следующая схема поможет с анализом этого конкретного примера.

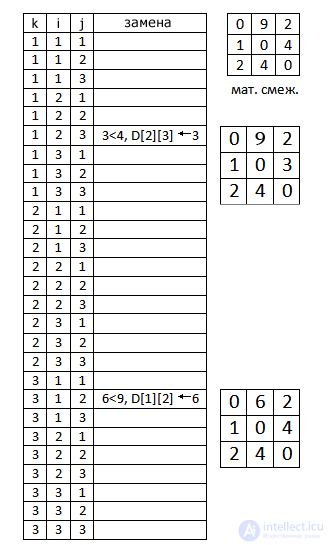
В данной таблице показаны 27 шагов выполнения основной части алгоритма. Их столько по той причине, что время выполнения метода равно O(|V|³). Наш граф имеет 3 вершины, а 3³=27. Первая замена происходит на итерации, при которой k=1, i=2, а j=3. В тот момент D =1, D =2, D =4. Условие истинно, т. е. D +D =3, а 3<4, следовательно, элемент матрицы D получает новое значение. Следующий шаг, когда условие также истинно привносит изменения в элемент, расположенный на пересечении второй строки и третьего столбца.

Оценка сложности

Время выполнения этой программы, очевидно, имеет порядок 0(V³), поскольку в ней практически нет ничего, кроме вложенных друг в друга трех циклов. Доказательство "правильности" работы этого алгоритма также очевидно и выполняется с помощью математической индукции по k, показывая, что на k-й итерации вершина k включается в путь только тогда, когда новый путь короче старого.

Пусть будет количеством вершин. Чтобы найти все из (для всех и ) из s требуется операций. Поскольку мы начинаем с и вычисляем последовательность матриц , , , , общее количество используемых операций равно . Следовательно, сложность алгоритма равна .

Сравнение с другими алгоритмами

Алгоритм Флойда–Уоршелла является эффективным для расчета всех кратчайших путей в плотных графах, когда имеет место большое количество пар ребер между парами вершин. В случае разреженных графов с ребрами неотрицательного веса лучшим выбором считается использование алгоритма Дейкстры для каждого возможного узла. При таком выборе сложность составляет при применении двоичной кучи, что лучше, чем алгоритма Флойда–Уоршелла тогда, когда существенно меньше (условие разреженности графа). Если граф разрежен, у него имеются ребра с отрицательным весом и отсутствуют циклы с отрицательным суммарным весом, то используется алгоритм Джонсона, который имеет ту же сложность, что и вариант с алгоритмом Дейкстры.

Также являются известными алгоритмы с применением алгоритмов быстрого перемножения матриц, которые ускоряют вычисления в плотных графах, но они обычно имеют дополнительные ограничения (например, представление весов ребер в виде малых целых чисел). Вместе с тем, из-за большого константного фактора времени выполнения преимущество при вычислениях над алгоритмом Флойда–Уоршелла проявляется только на больших графах.

применение и обобщения

Алгоритм Флойда–Уоршелла может быть использован для решения следующих задач, в частности:

• Кратчайшие пути в ориентированных графах (алгоритм Флойда).
• Транзитивное замыкание ориентированных графов (алгоритм Уоршелла). В оригинальной формулировке алгоритма Уоршелла граф не взвешен и представлен булевой матрицей смежности. Затем операция сложения заменяется логической конъюнкцией (И), а минимальная операция - логической дизъюнкцией (ИЛИ).
• Нахождение регулярного выражения, обозначающего регулярный язык, принимаемый конечным автоматом (алгоритм Клини, тесно связанное обобщение алгоритма Флойда–Уоршелла)
• Обращение вещественных матриц (алгоритм Гаусса–Жордана)
• Оптимальная маршрутизация. В этом приложении нужно найти путь с максимальным потоком между двумя вершинами. Это означает, что вместо взятия минимумов, как в псевдокоде выше, используются максимумы. Веса ребер представляют фиксированные ограничения для потока. Веса путей представляют собой узкие места поэтому операция сложения, указанная выше, заменяется минимальной операцией.
• Быстрый расчет сетей Pathfinder.
• Самые широкие пути/пути с максимальной пропускной способностью
• Вычисление канонической формы матриц разностных границ (DBMs)
• Вычисление сходства между графами

Вау!! 😲 Ты еще не читал? Это зря!

• динамический алгоритм
• динамическое программирование

На этом все! Теперь вы знаете все про алгоритм флойда - уоршелла, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое алгоритм флойда - уоршелла и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов