Нелинейное программирование кратко

Сразу хочу сказать, что здесь никакой воды про нелинейное программирование, и только нужная информация. Для того чтобы лучше понимать что такое нелинейное программирование , настоятельно рекомендую прочитать все из категории Математическое программирование.

нелинейное программирование (NLP, англ. NonLinear Programming) — случай математического программирования, в котором целевой функцией или ограничением является нелинейная функция.

Задача нелинейного программирования ставится как задача нахождения оптимума определенной целевой функции 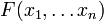при выполнении условий

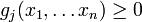
где 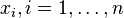— параметры, 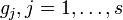— ограничения, — количество параметров, — количество ограничений.

В отличие от задачи линейного программирования, в задаче программирования нелинейного оптимум не обязательно лежит на границе области, определенной ограничениями.

задачи нелинейного программирования

Методы решения задачи

Одним из методов, которые позволяют свести задачу нелинейного программирования к решению системы уравнений, является метод неопределенных множителейЛагранжа.

Если целевая функция F является линейной, а ограниченным пространством является политоп, то задача является задачей линейного программирования, которая может быть решена с помощью хорошо известных решений линейного программирования.

Если целевая функция является вогнутой (задача максимизации) или выпуклой (задача минимизации) и множеством ограничений служит выпуклая, то задачу называют выпуклой, и в большинстве случаев могут быть использованы общие методы выпуклой оптимизации.

Если целевая функция является отношением вогнутых и выпуклых функций (при максимизации) и ограничения выпуклые, то задача может быть преобразована в задачу выпуклой оптимизации использованием техник дробного программирования.

Существуют несколько методов для решения невыпуклых задач. Об этом говорит сайт https://intellect.icu . Один подход заключается в использовании специальных формулировок задач линейного программирования. Другой метод предусматривает использование методов ветвей и границ, где задача делится на подклассы, чтобы быть решенной с выпуклыми (задача минимизации) или линейными аппроксимациями, которые образуют нижнюю границу общей стоимости в пределах раздела. При следующих разделах в определенный момент будет получено фактическое решение, стоимость которого равна лучшей нижней границе, полученной для любого из приближенных решений. Это решение является оптимальным, хотя, возможно, не единственным. Алгоритм можно прекратить на ранней стадии, с уверенностью, что оптимальное решение находится в рамках допустимого отклонения от найденной лучшей точки; такие точки называются ε-оптимальными. Завершение ε-оптимальных точек, как правило, необходимое для обеспечения конечности завершения. Это особенно полезно для больших, сложных задач и задач с неопределенными расходами или значениями, где неопределенность может быть определена из соответствующей оценки надежности.

Дифференцирование и условия регулярности, условия Каруша — Куна — Такера (ККТ) обеспечивают необходимые условия оптимальности решения. При выпуклости, эти условия являются и достаточными.

Вау!! 😲 Ты еще не читал? Это зря!

• Выпуклость в экономике
• Жадный алгоритм
• Невыпуклость ( экономика )
• Стохастическое программирование
• Стохастическое динамическое программирование
• Обучение с подкреплением
• динамическое программирование ,

А как ты думаешь, при улучшении нелинейное программирование, будет лучше нам? Надеюсь, что теперь ты понял что такое нелинейное программирование и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математическое программирование