Лекция
Сразу хочу сказать, что здесь никакой воды про линейное программирование, и только нужная информация. Для того чтобы лучше понимать что такое линейное программирование , настоятельно рекомендую прочитать все из категории Математическое программирование.
линейное программирование — математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах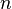 
-мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.
Линейное программирование является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования. Одновременно оно — основа нескольких методов решения задач целочисленного и нелинейного программирования. Одним из обобщений линейного программирования является дробно-линейное программирование.
Многие свойства задач линейного программирования можно интерпретировать также как свойства многогранников и таким образом геометрически формулировать и доказывать их.
Математические исследования отдельных экономических проблем, математическая формализация числового материала проводилась еще в XIX веке. Приматематическом анализе процесса расширенного производства использовались алгебраические соотношения, анализ их проводился с помощью дифференциального исчисления. Это давало возможность получить общее представление о проблеме.
Развитие экономики потребовало количественных показателей, и в 1920 годы был создан межотраслевой баланс (МОБ). Он то и послужил толчком в деле создания и исследования математических моделей. Разработка МОБ в 1924—1925 годах в СССР повлияла на работы экономиста и статистика Василия Васильевича Леонтьева. Он разработал межотраслевую модель производства и распределения продукции.
В 1938 году Леонид Витальевич Канторович в порядке научной консультации приступил к изучению чисто практической задачи по составлению наилучшего плана загрузки лущильных станков (фанерный трест). Эта задача не поддавалась обычным методам. Стало ясно, что задача не случайная.
В 1939 году Леонид Витальевич Канторович опубликовал работу «Математические методы организации и планирования производства», в которой сформулировал новый класс экстремальных задач с ограничениями и разработал эффективный метод их решения, таким образом были заложены основы линейного программирования.
Изучение подобных задач привело к созданию новой научной дисциплины линейного программирования и открыло новый этап в развитии экономико-математических методов.
В 1949 году американский математик Джордж Бернард Данциг разработал эффективный метод решения задач линейного программирования (ЗЛП) — симплекс-метод.
Термин «программирование» нужно понимать в смысле «планирования» (один из переводов англ. programming). Он был предложен в середине 1940-х годовДжорджем Данцигом, одним из основателей линейного программирования, еще до того, как компьютеры были использованы для решения линейных задачоптимизации.
Метод внутренних точек был впервые упомянут И. И. Дикиным в 1967 году.
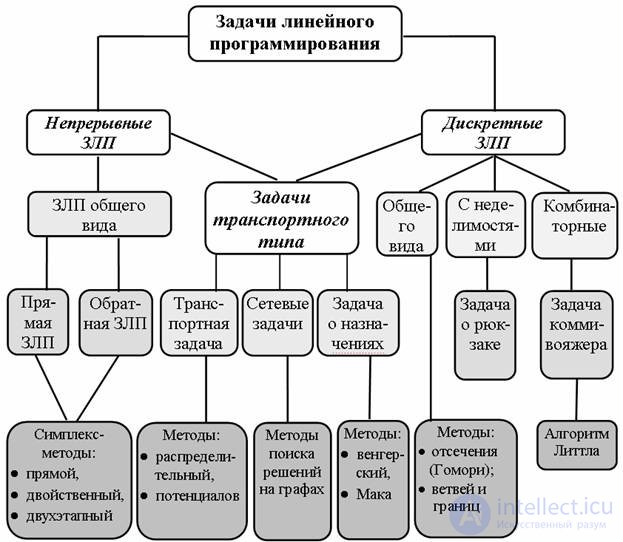
задачи линейного программирования
Общей (стандартной) задачей линейного программирования называется задача нахождения минимума линейной целевой функции (линейной формы) вида :
Задача, в которой фигурируют ограничения в форме неравенств, называется основной задачей линейного программирования (ОЗЛП)
,
.
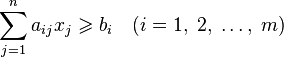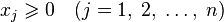Задача линейного программирования будет иметь канонический вид, если в основной задаче вместо первой системы неравенств имеет место система уравнений с ограничениями в форме равенства :
,
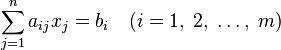Основную задачу можно свести к канонической путем введения дополнительных переменных.
Задачи линейного программирования наиболее общего вида (задачи со смешанными ограничениями: равенствами и неравенствами, наличием переменных, свободных от ограничений) могут быть приведены к эквивалентным (имеющим то же множество решений) заменами переменных и заменой равенств на пару неравенств .
Легко заметить, что задачу нахождения максимума можно заменить задачей нахождения минимума, взяв коэффициенты 
с обратным знаком.
Рассмотрим задачу о максимальном паросочетании в двудольном графе: есть несколько юношей и девушек, причем для каждых юноши и девушки известно, симпатичны ли они друг другу. Об этом говорит сайт https://intellect.icu . Нужно поженить максимальное число пар со взаимной симпатией.
Введем переменные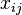 
, которые соответствуют паре из 
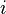-того юноши и 
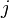-той девушки и удовлетворяют ограничениям:
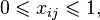
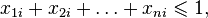
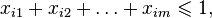
с целевой функцией 
. Можно показать, что среди оптимальных решений этой задачи найдется целочисленное. Переменные равные 1, будут соответствовать парам, которые следует поженить.
Пусть имеется граф (с ориентированными ребрами), в котором для каждого ребра указана его пропускная способность. И заданы две вершины: сток и исток. Нужно указать для каждого ребра, сколько через него будет протекать жидкости (не больше его пропускной способности) так, чтобы максимизировать суммарный поток из истока в сток (жидкость не может появляться или исчезать во всех вершинах, кроме истока и стока, соответственно).
Возьмем в качестве переменных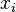 
— количество жидкости, протекающей через 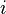-тое ребро. Тогда
,
где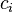 
— пропускная способность 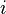-того ребра. Эти неравенства надо дополнить равенством количества втекающей и вытекающей жидкости для каждой вершины, кроме стока и истока. В качестве функции 
естественно взять разность между количеством вытекающей и втекающей жидкости в истоке.
Обобщение предыдущей задачи — максимальный поток минимальной стоимости. В этой задаче даны стоимости для каждого ребра и нужно среди максимальных потоков выбрать поток с минимальной стоимостью. Эта задача сводится к двум задачам линейного программирования: сначала нужно решить задачу о максимальном потоке, а потом добавить к этой задаче ограничени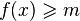е 
, где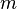 
— величина максимального потока, и решить задачу с новой функцией 
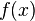— стоимостью потока.
Эти задачи могут быть решены быстрее, чем общими алгоритмами решения задач линейного программирования, за счет особой структуры уравнений и неравенств.
Имеется некий однородный груз, который нужно перевезти с 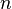складов на 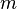заводов. Для каждого склада 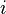известно, сколько в нем находится груза 
, а для каждого завода известна его потребность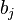 
в грузе. Стоимость перевозки пропорциональна расстоянию от склада до завода (все расстояния 
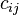от 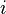-го склада до 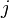-го завода известны). Требуется составить наиболее дешевый план перевозки.
Решающими переменными в данном случае являются 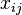— количества груза, перевезенного из 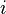-го склада на 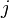-й завод. Они удовлетворяют ограничениям:
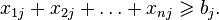
Целевая функция имеет вид: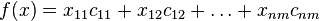 
, которую надо минимизировать.
Есть матрица 
размера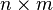 
. Первый игрок выбирает число от 1 до 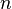, второй — от 1 до 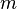. Затем они сверяют числа и первый игрок получает 
очков, а второй 
очков (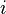 — число, выбранное первым игроком, 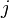— вторым). Нужно найти оптимальную стратегию первого игрока.
Пусть в оптимальной стратегии, например, первого игрока число 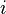нужно выбирать с вероятностью 
. Тогда оптимальная стратегия является решением следующей задачи линейного программирования:
,
,
(
),
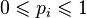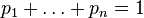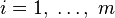в которой нужно максимизировать функцию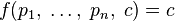 
. Значение в оптимальном решении будет математическим ожиданием выигрыша первого игрока в наихудшем случае.
Наиболее известным и широко применяемым на практике для решения общей задачи линейного программирования (ЛП) является симплекс-метод. Несмотря на то, что симплекс-метод является достаточно эффективным алгоритмом, показавшим хорошие результаты при решении прикладных задач ЛП, он является алгоритмом сэкспоненциальной сложностью. Причина этого состоит в комбинаторном характере симплекс-метода, последовательно перебирающего вершины многогранникадопустимых решений при поиске оптимального решения.
Первый полиномиальный алгоритм, метод эллипсоидов, был предложен в 1979 году советским математиком Л. Хачияном, разрешив таким образом проблему, долгое время остававшуюся нерешенной. Метод эллипсоидов имеет совершенно другую, некомбинаторную природу, нежели симплекс-метод. Однако в вычислительном плане этот метод оказался неперспективным. Тем не менее, сам факт полиномиальной сложности задач привел к созданию целого класса эффективных алгоритмов ЛП — методов внутренней точки, первым из которых был алгоритм Н. Кармаркара, предложенный в 1984 году. Алгоритмы этого типа используют непрерывную трактовку задачи ЛП, когда вместо перебора вершин многогранника решений задачи ЛП осуществляется поиск вдоль траекторий в пространстве переменных задачи, не проходящих через вершины многогранника. Метод внутренних точек, который, в отличие от симплекс-метода, обходит точки из внутренней части области допустимых значений, использует методы логарифмических барьерных функций нелинейного программирования, разработанные в 1960-х годах Фиако (Fiacco) и МакКормиком (McCormick).
А как ты думаешь, при улучшении линейное программирование, будет лучше нам? Надеюсь, что теперь ты понял что такое линейное программирование и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математическое программирование
Из статьи мы узнали кратко, но содержательно про линейное программирование
Комментарии
Оставить комментарий
Математическое программирование
Термины: Математическое программирование