Лекция
Привет, сегодня поговорим про граф ма тика , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое граф ма тика , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
Граф — основной объект изучения математической теории графов, совокупность непустого множества вершин и наборов пар вершин (связей между вершинами).
Объекты представляются как вершины, или узлы графа, а связи — как дуги, или ребра[1]. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или ребрах.
Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами. Например, строение Википедии можно смоделировать при помощи ориентированного графа (орграф), в котором вершины — это статьи, а дуги (ориентированные ребра) — гиперссылки (тематическая карта).
Теория графов не обладает устоявшейся терминологией. В различных статьях под одними и теми же терминами понимаются разные вещи. Ниже приведены наиболее часто встречаемые определения.
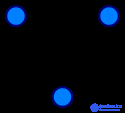
Граф, или неориентированный граф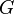 
— это упорядоченная пара 
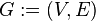, где 
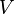— это непустое множество вершин или узлов, а 
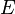— множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых ребрами.
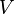(а значит и, 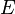, иначе оно было бы мультимножеством) обычно считаются конечными множествами. Многие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов, поскольку не все утверждения, имеющие место для конечных совокупностей, выполняются в случае бесконечных множеств.
Вершины и ребра графа называются также элементами графа, число вершин в графе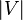 
— порядком, число ребер 
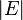— размером графа.
Вершины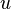 
и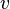 
называются концевыми вершинами (или просто концами) ребра 
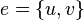. Ребро, в свою очередь , соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.
Два ребра называются смежными, если они имеют общую концевую вершину.
Два ребра называются кратными, если множества их концевых вершин совпадают.
Ребро называется петлей, если его концы совпадают, то есть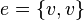 
.
Степенью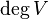 
вершины 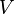называют количество инцидентных ей ребер (при этом петли считают дважды).
Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.
Ориентированный граф (сокращенно орграф) 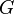— это упорядоченная пара 
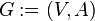, где 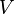— непустое множество вершин или узлов, и 
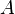— множество (упорядоченных) пар различных ребер, называемых дугами или ориентированными ребрами.
Дуга — это упорядоченная пара вершин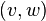 
, где вершину 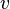называют началом, а 
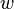— концом дуги. Об этом говорит сайт https://intellect.icu . Можно сказать, что дуга 
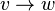ведет от вершины 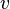к вершине .
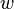Смешанный граф 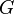— это граф, в котором некоторые ребра могут быть ориентированными, а некоторые — неориентированными. Записывается упорядоченной тройкой 
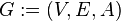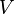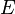, где , и 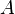определены так же, как выше.
Ориентированный и неориентированный графы являются частными случаями смешанного.
Граф 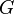называется изоморфным графу 
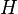, если существует биекция 
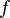из множества вершин графа 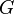в множество вершин графа 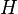, обладающая следующим свойством: если в графе 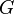есть ребро из вершины 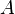в вершину 
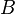, то в графе 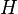должно быть ребро из вершины 
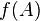в вершину 
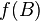и наоборот — если в графе 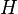есть ребро из вершины 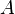в вершину 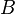, то в графе 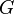должно быть ребро из вершины 
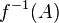в вершину 
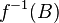. В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.
Маршрутом в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершиной ребром. Цепью называется маршрут без повторяющихся ребер. Простой цепью называется маршрут без повторяющихся вершин (откуда следует, что в простой цепи нет повторяющихся ребер).
Ориентированным маршрутом (или путем) в орграфе называют конечную последовательность вершин и дуг, в которой каждый элемент инцидентен предыдущему и последующему.
Циклом называют цепь, в которой первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его ребер. Заметим, что если вершины 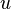и 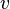являются концами некоторого ребра, то согласно данному определению, последовательность 
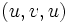является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.
Путь (или цикл) называют простым, если ребра в нем не повторяются; элементарным, если он простой и вершины в нем не повторяются. Нетрудно видеть, что:
Бинарное отношение на множестве вершин графа, заданное как «существует путь из 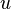в 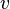», является отношением эквивалентности и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.
Всякий максимальный связный подграф графа G называется связной компонентой (или просто компонентой) графа 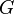. Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов
Ребро графа называется мостом, если его удаление увеличивает число компонент.
Граф называется:
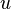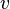, есть путь из 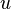в .
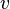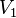и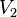 
так, что всякое ребро соединяет вершину из 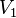с вершиной из .
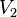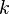непересекающихся подмножества , , …, 
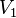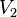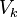так, что не будет ребер, соединяющих вершины одного и того же подмножества.Также бывает:
Простой граф является одномерным симплициальным комплексом.
Более абстрактно, граф можно задать как тройку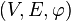 
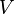, где и 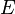— некоторые множества (вершин и ребер, соотв.), а 
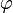— функция инцидентности (илиинцидентор), сопоставляющая каждому ребру 
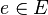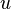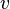(упорядоченную или неупорядоченную) пару вершин и из 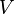(его концов). Частными случаями этого понятия являются:
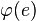всегда является упорядоченной парой вершин; 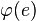всегда является неупорядоченной парой вершин;Под данное выше определение не подходят некоторые другие обобщения :
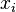и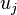 
существуют бинарные отношения инцидентности.Таблица, где как столбцы, так и строки соответствуют вершинам графа. В каждой ячейке этой матрицы записывается число , определяющее наличие связи от вершины-строки к вершине-столбцу (либо наоборот).
Недостатком являются требования к памяти, прямо пропорциональные квадрату количества вершин.
Каждая строка соответствует определенной вершине графа, а столбцы соответствуют связям графа. В ячейку на пересечении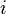 
-ой строки с 
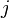-м столбцом матрицы записывается:
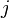«выходит» из вершины 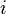,Данный способ является самым емким (размер пропорционален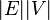 
) для хранения, но облегчает нахождение циклов в графе.
Список ребер — это тип представления графа, подразумевающий, что каждое ребро представляется двумя числами — номерами вершин этого ребра.
Для описания графов в целях, пригодных для машинной обработки и одновременно удобном для человеческого восприятия используется несколько стандартизированных языков, среди которых:
Разработана серия коммерческих программ для построения графов, так, построение графов лежит в основе прикладных программных пакетов фирмы ILOG (с 2009 года принадлежит корпорации IBM), среди других программ — GoView, Lassalle AddFlow, LEDA (есть бесплатная редакция).
Также существует свободная программа для построения графов igraph и свободная библиотека Boost (свободное ПО).
Для визуализации графов можно использовать:
На этом все! Теперь вы знаете все про граф ма тика , Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое граф ма тика и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.