Лекция
Привет, сегодня поговорим про субфакториал, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое субфакториал , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
субфакториал числа n (обозначение: !n) определяется как количество беспорядков порядка n, то есть перестановок порядка n без неподвижных точек. Название субфакториал происходит из аналогии с факториалом, определяющим общее количество перестановок.
В частности, !n есть число способов положить n писем в n конвертов (по одному в каждый), чтобы ни одно не попало в соответствующий конверт (т. н. Задача о письмах).
Субфакториал — это математическая функция, которая определяется как количество перестановок из n элементов, которые не имеют ни одной фиксированной точки. Символически субфакториал обозначается как !n.
Например, если у нас есть три элемента {1, 2, 3}, то мы можем получить 3! = 6 перестановок: (1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2), (3,2,1). Однако, если мы хотим получить перестановки без фиксированных точек, то они могут быть только две: (2,3,1) и (3,1,2). Это означает, что !3 = 2.
Субфакториал можно вычислить с помощью принципа включения-исключения:
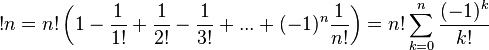
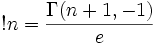 , где
, где 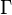 обозначает неполную гамма-функцию (англ.), а e — математическая константа;
обозначает неполную гамма-функцию (англ.), а e — математическая константа;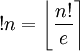 , где
, где 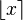 обозначает ближайшее к x целое число.
обозначает ближайшее к x целое число.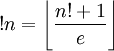 (согласно Mehdi Hassani), где
(согласно Mehdi Hassani), где 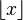 обозначает целую часть числа.
обозначает целую часть числа.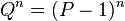 и
и 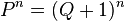 , где
, где 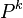 нужно понимать как
нужно понимать как 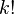 , а
, а 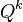 — как
— как  .
. 
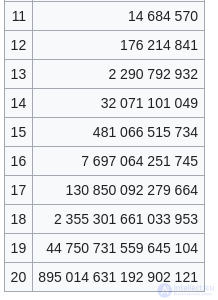
последовательность A000166 в OEIS
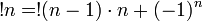
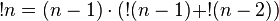 (таким же свойством обладает сам факториал)
(таким же свойством обладает сам факториал)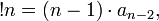
где 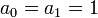 и
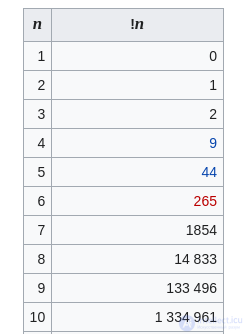
и 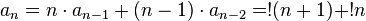 . Об этом говорит сайт https://intellect.icu . Начальные члены последовательности
. Об этом говорит сайт https://intellect.icu . Начальные члены последовательности 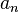 :
:
1, 1, 3, 11, 53, 309, 2119, … (последовательность A000255 в OEIS)
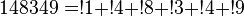 (найдено J. S. Madachy, 1979)
(найдено J. S. Madachy, 1979)
Итак, если факториал определяет количество перестановок, возможных в наборе из n объектов, то субфакториал характеризует количество беспорядков в таком же наборе. Проще всего понять, что такое факториал на жизненном примере. Возьмем некоторое количество писем и конвертов и пронумеруем их:
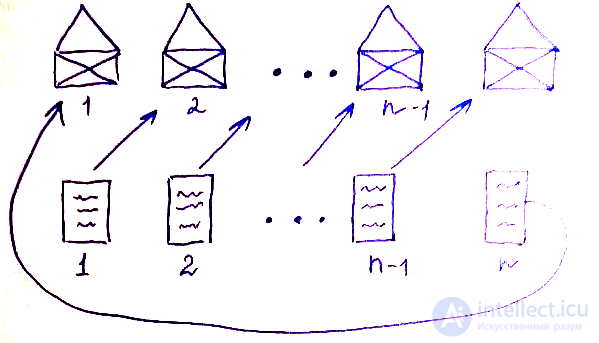
Теперь наша задача в том, чтобы создать максимальный беспорядок, а именно сделать так, чтобы каждое письмо оказалось не в том конверте, для которого предназначено. На рисунке я показал один из способов такого распределения.
Вы уже, наверное, догадались, что именно субфакториал определит количество таких возможных перестановок, в комбинаторике называемых смещениями.
Формула для вычисления субфакториала сложностью не отличается:
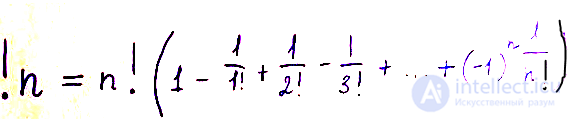
Формула была выведена Николаем Бернулли еще в 1713 году.
Единственное, что восклицательный знак ставится перед переменной. Для примера вычислим !4:
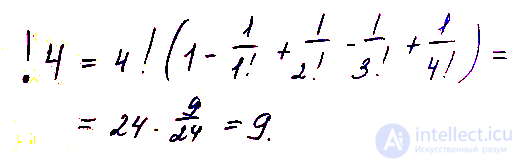
Значит, в наборе из 4 писем есть 9 вариантов навести тотальный хаос!
Еще одна интерпретация задачи: профессор дал тест 4 студентам – 1, 2, 3 и 4 – и хочет, чтобы они оценили тесты друг друга. Конечно, ни один студент не должен оценивать свой собственный тест. Сколько существует способов, чтобы никто не получил обратно свой собственный тест для проверки?
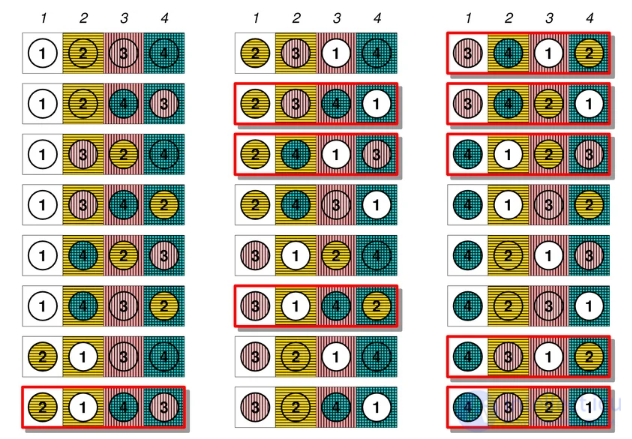
Видно, что таких случаев 9, как и должно быть по формуле.Источник: https://upload.wikimedia.org/wikipedia/commons/thumb/f/f1/Derangement4.png/800px-Derangement4.png
Судя по формуле, субфакториал всегда меньше факториала, ведь в скобках величина всегда меньшая, чем 1/2 для n>3. Поразительно, но факториал и субфакторила лаконично связаны через постоянную Эйлера, и это действительно очень красиво:
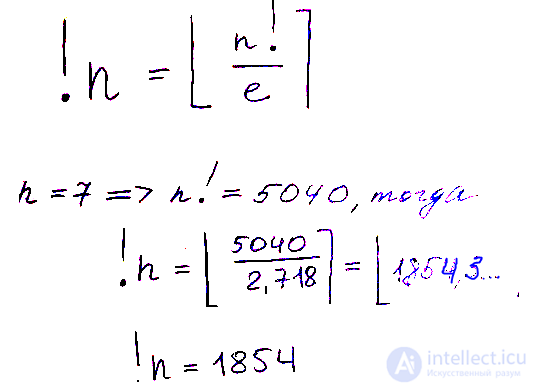
Просто вычисляем ближайшее целое число к полученному результату
Ну и напоследок еще одно феноменальное совпадение - единственное известное математикам число-субфакторион:
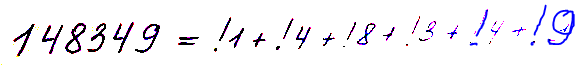
Субфакториал имеет практическое применение в различных областях, таких как комбинаторика, криптография, теория графов, теория вероятностей и других. Например, в криптографии субфакториал используется для вычисления количества ключей, которые необходимы для шифрования данных, чтобы никакой ключ не использовался дважды. В теории графов субфакториал используется для определения числа гамильтоновых путей и циклов в графе.
Также стоит отметить, что субфакториал является частным случаем обычного факториала. Факториал n обозначается как n! и определяется как произведение всех целых чисел от 1 до n. Следовательно, !n можно выразить через n! следующим образом: !n = n! * S(n, 1), где S(n, k) - количество стерлинговых чисел второго рода, которые определяют количество способов разбить множество из n элементов на k непустых подмножеств.
субфакториал - это математическая функция, которая имеет широкое практическое применение в различных областях. Знание этой функции может быть полезным для людей, работающих в таких областях, как криптография, теория графов и теория вероятностей.
На этом все! Теперь вы знаете все про субфакториал, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое субфакториал и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Из статьи мы узнали кратко, но содержательно про субфакториал
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.