Лекция
Привет, Вы узнаете о том , что такое функциональная полнота, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое функциональная полнота , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
функциональная полнота множества логических операций или булевых функций — это возможность выразить все возможные значения таблиц истинности с помощью формул из элементов этого множества. Математическая логика обычно использует такой набор операций: конъюнкция (), дизъюнкция (
), отрицание (
), импликация (
) и эквиваленция (
). Это множество операций является функционально полным. Но оно не является минимальной функционально полной системой, поскольку:
Таким образом также является функционально полной системой. Но
также может быть выражено (в соответствии с законом де Моргана) как:
также может быть определена через
подобным образом.
Также может быть выражена через
следующим образом:
Итак и одна из
является минимальной функционально полной системой.

Критерий Поста описывает необходимые и достаточные условия функциональной полноты множеств булевых функций. Об этом говорит сайт https://intellect.icu . Был сформулирован американским математиком Эмилем Постом в 1941 году.
Критерий:
Множество булевых функций является функционально полным тогда и только тогда, когда оно не содержится полностью ни в одном из предполных классов.
Критерий полноты (Теорема Поста): Система S булевых функций является полной тогда и только тогда, когда она включает хотя бы одну функцию: не сохраняющую константу 0, не сохраняющую константу 1, не самодвойственную, нелинейную и немонотонную.
В таблице приведены свойства, которыми обладают элементарные булевы функции (символ * - отмечает свойство, которым обладает данная функция).
| Название | Обозначение |
Не сохранимость константы 0 |
Не сохранимость константы 1 |
Не самодвойственность |
Не линейность |
Не монотонность |
| Конст. 0 | 0 | * | * | |||
| Конст. 1 | 1 | * | * | |||
| Отриц. | ¬ | * | * | * | ||
| Конъюн. | & | * | * | |||
| Дизъюн. | v | * | * | |||
| Имплик. | → | * | * | * | * | |
| Эквивал. | ∼ | * | * | * | ||
| Сумма по мод. 2 | ⊕ | * | * | * | ||
| Штрих Шеффера | | | * | * | * | * | * |
| Стрелка Пирса | ↓ | * | * | * | * | * |
Используя теорему Поста и данную таблицу можно строить базисы из элементарных функций по следующему правилу. Выбрав любую элементарную булеву функцию и дополнив ее при необходимости другими функциями так, чтобы все они вместе удовлетворяли теореме о функциональной полноте. Через функции этого базиса можно выразить все другие булевы функции.
Множества из одного элемента
(штрих Шеффера),
(стрелка Пирса)
Множества двух элементов
Множества трех элементов
,
(см. алгебра Жегалкина),
(инверсный к предыдущему)
Определение. Множество функций N называется функционально полной системой (ФПС), если любая булева функция представима суперпозицией функций из N.
Договоримся опускать аргументы при перечислении функций множества N и рассматривать термин ''система'' в данном контексте как синоним множества.
Пример 1. Множество N1={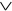 ,
, 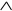 , –} является функционально полной системой, так как любую булеву функцию, кроме константы 0, можно представить совершенной ДНФ, то есть суперпозицией функций из N1 а константу 0 – формулой xx . •
, –} является функционально полной системой, так как любую булеву функцию, кроме константы 0, можно представить совершенной ДНФ, то есть суперпозицией функций из N1 а константу 0 – формулой xx . •
Пример 2. Множество N2={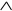 ,
, 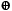 , 1} является ФПС, так как любую булеву функцию можно представить полиномом Жегалкина, то есть суперпозицией функций из N2, а полином 0 – формулой 1
, 1} является ФПС, так как любую булеву функцию можно представить полиномом Жегалкина, то есть суперпозицией функций из N2, а полином 0 – формулой 1 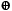 1. •
1. •
Следующая теорема позволяет сводить вопрос о функциональной полноте одних систем к вопросу о полноте других систем.
Теорема о двух функционально полных системах. Если даны два множества N1 и N2 булевых функций и известно, что N1 – функционально полная система, а каждая функция из N1 представима суперпозицией функций из N2, то N2тоже является функционально полной системой.
Доказательство. Рассмотрим произвольную булеву функцию f(x1, …, xn). Она может быть представлена суперпозицией функций из множества N1={f0,f1 …, fm}, так как N1 – ФПС:
По условию теоремы каждая из функций f0, f1 …, fm может быть представлена суперпозицией функций из N2, значит, функция f(x1, …, xn) представима суперпозицией функций из N2, следовательно, N2 – ФПС. •
Пример 1. N1={ 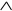 , –,
, –,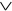 }, N2={
}, N2={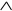 , –}. Как показано ранее, N1 – ФПС. Конъюнкция и инверсия содержатся в N2, а дизъюнкция представима суперпозицией функций из N2: x
, –}. Как показано ранее, N1 – ФПС. Конъюнкция и инверсия содержатся в N2, а дизъюнкция представима суперпозицией функций из N2: x 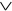 y =
y = 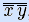 , значит, N2 – ФПС. •
, значит, N2 – ФПС. •
Пример 2. N1={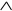 , –}, N2={↓ }. Как показано в предыдущем примере, N1 – ФПС. Инверсия и конъюнкция могут быть представлены суперпозицией стрелки Пирса: x = x↓ x, xy =
, –}, N2={↓ }. Как показано в предыдущем примере, N1 – ФПС. Инверсия и конъюнкция могут быть представлены суперпозицией стрелки Пирса: x = x↓ x, xy =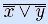 = (x↓ x)↓ (y↓ y), следовательно N2 – ФПС. •
= (x↓ x)↓ (y↓ y), следовательно N2 – ФПС. •
Исследование, описанное в статье про функциональная полнота, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое функциональная полнота и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Из статьи мы узнали кратко, но содержательно про функциональная полнота
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.