Лекция
Привет, сегодня поговорим про разбиение множества, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое разбиение множества, множества множеств, разбиение на классы множеств , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
разбиение множества — это представление его в виде объединения произвольного количества попарно непересекающихся подмножеств.
Пусть 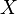 — произвольное множество. Семейство непустых множеств
— произвольное множество. Семейство непустых множеств 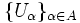 , где
, где 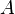 — некоторое множество индексов (конечное или бесконечное), называется разбиением
— некоторое множество индексов (конечное или бесконечное), называется разбиением 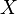 , если:
, если:
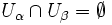 для любых
для любых 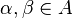 , таких что
, таких что 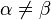 ;
;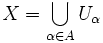 .
.При этом множества 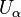 называются блоками или частями разбиения данного множества
называются блоками или частями разбиения данного множества 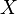 .
.

Традиционные японские символы для 54 глав « Повести о Гэндзи» основаны на 52 способах разделения пяти элементов (два красных символа представляют одно и то же разделение, а зеленый символ добавляется при достижении 54).
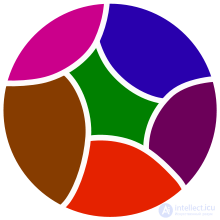
Рисунок 1 - пример разбиения множества.
Разбиения конечных множеств, а также подсчет количества различных разбиений, удовлетворяющих тем или иным условиям, представляет особый интерес вкомбинаторике. В частности, некоторые комбинаторные функции естественно возникают как количества разбиений того или иного вида.
Например, число Стирлинга второго рода 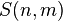 представляет собой количество неупорядоченных разбиений n-элементного множества на m частей, в то время какмультиномиальный коэффициент
представляет собой количество неупорядоченных разбиений n-элементного множества на m частей, в то время какмультиномиальный коэффициент 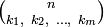 выражает количество упорядоченных разбиений n-элементного множества на m частей фиксированного размера
выражает количество упорядоченных разбиений n-элементного множества на m частей фиксированного размера 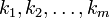 . Количество всех неупорядоченных разбиений n-элементного множества задается числом Белла
. Количество всех неупорядоченных разбиений n-элементного множества задается числом Белла 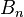 .
.
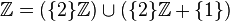 , где
, где  — множества всех целых чисел, четных целых чисел и нечетных целых чисел соответственно;
— множества всех целых чисел, четных целых чисел и нечетных целых чисел соответственно; может быть представлено в виде:
может быть представлено в виде:  ;
; может быть разбито пятью способами:
может быть разбито пятью способами: 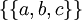 ,
,  ,
, 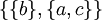 ,
, 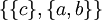 ,
, 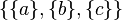 — значит, число Белла
— значит, число Белла  .
.Мы можем рассматривать множества, состоящие из самых различных элементов. Об этом говорит сайт https://intellect.icu . В частности, можем рассматривать множества множеств, т. е. множества, элементы которых сами суть множества. Таково, например, множество всех пар весел, имеющихся на данной лодочной станции. Множеством множеств является также множество всех спортивных команд города Н. (каждая спортивная команда есть множество составляющих ее спортсменов).
Множество всех профессиональных союзов, а также множество всех воинских частей (дивизий, полков, батальонов, рот, взводов и т. д.) данной армии являются множествами множеств. Эти примеры показывают, что множества, являющиеся элементами данного множества множеств, могут в одних случаях пересекаться, в других случаях, наоборот, не иметь общих элементов.
Так, например, множество всех партий страны есть множество попарно не пересекающихся множеств, так как гражданин не может быть одновременно членом двух политическирх партий. С другой стороны, множество всех воинских частей какой-либо армии есть пример множества множеств, некоторые элементы которого являются подмножествами других элементов: так, каждый взвод есть подмножество некоторого полка, полк есть подмножество дивизии и т. д.
Множество спортивных команд данного города состоит, вообще говоря, из пересекающихся множеств, так как одно и то же лицо может входить в несколько спортивных команд (например, в команду пловцов и в команду волейболистов или лыжников).
Замечание. Для облегчения речи иногда вместо выражения «множество множеств» употребляются как совершенно равнозначащие выражения «система множеств» или «совокупность множеств».
Понятие множества и операций над множествами позволяют уточнить представление о классификации.
Классификация – это действие распределения объектов по классам на основании сходств внутри класса и их отличия от других объектов. Классификация широко применяется в математике.
Например, натуральные числа делятся на четные и нечетные; углы бывают острые, тупые и прямые и т.д.
Любая классификация связана с разбиением некоторого множества объектов на подмножества.
Считают, что множество Х разбито на классы Х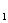 , Х
, Х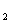 ,…, Х
,…, Х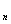 , если:
, если:
1) подмножества Х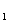 , Х
, Х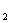 ,…, Х
,…, Х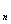 попарно не пересекаются;
попарно не пересекаются;
2) объединение этих подмножеств совпадает с множеством Х.
Если не выполнено хотя бы одно из этих условий, классификацию считают неправильной.
Например: а) Множество треугольников Х разбито на три класса: остроугольные, прямоугольные и тупоугольные. Действительно, выделенные подмножества попарно не пересекаются, а их объединение совпадает с множеством Х; b) Из множества треугольников Х выделили подмножества равнобедренных, равносторонних и разносторонних треугольников. Так как множества равнобедренных и равносторонних треугольников пересекаются, значит, не выполнено первое условие классификации, и разбиения множества Х на классы мы не получили.
Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять при помощи свойств элементов множеств.
Рассмотрим, например, множество натуральных чисел. Его элементы обладают различными свойствами. Нас интересуют числа со свойством «быть кратным 3». Это свойство позволяет выделить из множества N подмножество, состоящее из чисел, кратных 3. Тогда про остальные натуральные числа можно сказать, что они не кратны 3, т.е. получаем еще одно подмножество множества N. Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством N, то имеем разбиение данного множества на два класса.
Вообще, если на множестве Х задано одно свойство, то это множество разбивается на два класса. Первый – это класс объектов, обладающих данным свойством, а второй – дополнение первого класса до множества Х. Во втором классе содержатся такие объекты множества Х, которые заданным свойством не обладают. Такую классификацию называют дихотомической.
Рассмотрим ситуацию, когда для элементов множества заданы два свойства. Например, свойства натуральных чисел: «быть кратным 3» и «быть кратным 5». При помощи этих свойств из множества N можно выделить два подмножества: А – множество чисел, кратных 3 и В – множество чисел, кратных 5. Эти множества пересекаются, но ни одно из них не является подмножеством другого (рис. 13). Разбиения на подмножества А и В в данном случае на произошло. Но круг, изображающий множество N, можно рассматривать как состоящий из четырех непересекающихся областей. Каждая область изображает некоторое подмножество множество N. Множество I состоит из чисел, кратных 3 и 5, множество I – из чисел, кратных 3 и не кратных 5, множество III – из чисел, кратных 5 и не кратных 3, множество IV – из чисел, не кратных 3 и не кратных 5. Объединение этих четырех множеств есть множество N.
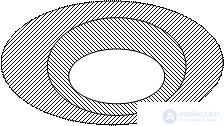 Таким образом, выделение двух свойств привело к разбиению множества N натуральных чисел на четыре класса.
Таким образом, выделение двух свойств привело к разбиению множества N натуральных чисел на четыре класса.
Не следует думать, что задание двух свойств элементов множества всегда приводит к разбиению этого множества на четыре класса. Например, при помощи таких двух свойств «быть кратным 3» и «быть кратным 6» множество натуральных чисел разбивается
на три класса (рис. 14): I – класс чисел, кратных 6; II – класс чисел, кратных 3, но не кратных 6; III – класс чисел, не кратных 3.
Очень важный класс систем множеств получаем, если рассматриваем всевозможные разбиения какого-нибудь множества на попарно не пересекающиеся множества. Дано множество X, представленное в виде суммы попарно не пересекающихся подмножеств; множества, слагаемые нашей суммы, и являются элементами данного разбиения множества X.
Пример 1. М есть множество всех учащихся в средних школах Москвы. Множество М можно разбить на попарно не пересекающиеся подмножества, например, следующими двумя способами:
1) мы объединяем в одно слагаемое всех учащихся одной и той же школы (т. е. разбиваем множество всех учащихся по школам);
2) мы объединяем в одно слагаемое всех учащихся одного и того же класса (хотя бы и разных школ).
Пример 2. Пусть X есть множество всех точек плоскости; возьмем на этой плоскости какую-нибудь прямую g и разобьем всю плоскость на прямые, параллельные прямой g. Множества точек каждой такой прямой и являются теми подмножествами, на которые мы разбиваем множество X.
Если данное множество X разбито на попарно не пересекающиеся подмножества, дающие в сумме множество М, то для краткости говорят просто о разбиении множества М на классы.
Задача разбиения множества чисел — это задача определения, можно ли данное мультимножество S положительных целых чисел разбить на два подмножества S1 и S2, таких, что сумма чисел из S1 равна сумме чисел из S2. Хотя задача разбиения чисел является NP-полной, существует решение псевдополиномиального времени методом динамического программирования и существуют эвристические алгоритмы решения для многих конкрентных задач либо оптимально, либо приближенно. По этой причине задачу называют "простейшей NP-трудной задачей" .
Существует оптимизационная версия задачи разбиения, в которой требуется разбить мультимножество S на два подмножества S1 и S2, таких, что разность между суммой элементов S1 и суммой элементов S2 минимальна. Оптимизационная версия является NP-трудной задачей, но на практике может быть решена эффективно .
Если дано множество S={3,1,1,2,2,1}, допустимым решением задачи разбиения являются два множества S1={1,1,1,2} и S2={2,3}. Оба множества имеют сумму 5, и они являются разбиением множества S. Заметим, что это решение не уникально. S1={3,1,1} и S2={2,2,1} является другим решением.
Не любое мультимножество положительных целых чисел имеет разбиение на две части с равными суммами. Пример такого множества — S={2,5}.
Общее количество разбиений n -элементного набора - это Белловское число B n . Первые несколько чисел Белла: B 0 = 1, B 1 = 1, B 2 = 2, B 3 = 5, B 4 = 15, B 5 = 52 и B 6 = 203 (последовательность A000110 в OEIS ). Числа Белла удовлетворяют рекурсии
и имеют экспоненциальную производящую функцию
Количество разбиений n -элементного набора ровно на k (непустых) частей - это число Стирлинга второго рода S ( n , k ).Числа Белла также могут быть вычислены с использованием треугольника Белла, в котором первое значение в каждой строке копируется из конца предыдущей строки, а последующие значения вычисляются путем добавления двух чисел, числа слева и числа к указанному выше. слева от позиции. Числа Белла повторяются по обеим сторонам этого треугольника. Числа внутри треугольника подсчитывают разделы, в которых данный элемент является наибольшим синглтоном .
Количество непересекающихся разделов набора n -элементов - это каталонское число.
Надеюсь, эта статья про разбиение множества, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое разбиение множества, множества множеств, разбиение на классы множеств и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.