Лекция
Привет, Вы узнаете о том , что такое топология, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое топология, топологическое пространство, база топологии , настоятельно рекомендую прочитать все из категории Функциональный анализ.
Топологи́ческое простра́нство — множество с дополнительной структурой определенного типа (так называемой топологией); является основным объектом изучения топологии.
Исторически понятие топологического пространства появилось как обобщение метрического пространства. Топологические пространства естественным образом возникают почти во всех разделах математики. Среди дальнейших обобщений представлений о множестве с пространственной структурой — псевдо топологическое пространство .
Пусть дано множество . Система
его подмножеств называется тополо́гией на
, если выполнены следующие условия:
Пара называется топологическим пространством. Множества, принадлежащие
, называются открытыми множествами.
Множества, являющиеся дополнениями к открытым, называются замкнутыми.
Всякое открытое множество, содержащее данную точку, называется ее окрестностью.
Три аксиомы, определяющие общий класс топологических пространств, часто дополняются теми или иными аксиомами отделимости, в зависимости от которых выделяют различные классы топологических пространств, например, тихоновские пространства, хаусдорфовы пространства, регулярные, вполне регулярные, нормальные пространства и др.
Кроме этого, на свойства топологических пространств сильно влияет выполнение тех или иных аксиом счетности — первая аксиома счетности, вторая аксиома счетности (пространства со счетной базой топологии), а также сепарабельность пространства. Из наличия счетной базы топологии следует сепарабельность и выполнение первой аксиомы счетности. Кроме того, например, регулярные пространства со счетной базой являются нормальными и, более того, метризуемы, то есть их топология может быть задана некоторой метрикой. Для компактных хаусдорфовых пространств наличие счетной базы топологии является необходимым и достаточным условием метризуемости. Для метрических пространств наличие счетной базы топологии и сепарабельность — эквивалентны.
Определение 1 (основное определение). Пусть Х – произвольное множество и t = {U} – совокупность его подмножеств, обладающая следующими свойствами (аксиомы топологии):
1) Æ, Х Î t;
2) объединение любой совокупности множеств из t принадлежит t;
3) пересечение любого конечного числа множеств из t принадлежит t.
Такая совокупность подмножеств t называется топологией на X. Множество Х с заданной на нем топологией t называется топологическим пространством и обозначается (X, t), подмножества из совокупности t называются открытыми (в пространстве (X, t)).
Пример 1. Х – числовая прямая R1. Топологию на R1 можно задать следующим набором подмножеств: пустое множество Æ, всевозможные интервалы и их объединения U = 
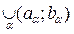 . Аксиомы топологии проверяются несложно.
. Аксиомы топологии проверяются несложно.
Пример 2. X = R2. Открытым множеством назовем всякое множество в X = R2, которое вместе с каждой своей точкой содержит достаточно малый открытый круг с центром в этой точке, а также пустое множество. Это определение соответствует стандартному пониманию открытых множеств, даваемому в курсе «Математического анализа». Легко проверить, что система всех открытых множеств в Х = R2 образует топологию.
Пример 3. Х – произвольное множество. Совокупность tmin = {Æ, X} очевидно задает топологию на Х. Таким образом определенная топология на Х называется минимальной или тривиальной.
Пример 4. Х – произвольное множество, tmax = {всевозможные подмножества X}. Совокупность t – топология на Х. Эта топология называется максимальной или дискретной.
Таким образом, на одном и том же множестве можно ввести различные топологии, например, тривиальную и дискретную.
С понятием открытого множества в топологическом пространстве (X, t) тесно связано двойственное понятие замкнутого множества: так называют множество, дополнение которого до Х открыто. Иными словами, если U Î t, то X\U замкнуто, и обратно: если F замкнуто, то X\F открыто.
В силу двойственного характера операций в теории множеств совокупность {F} всех замкнутых множеств топологического пространства (X, t) удовлетворяет следующим свойствам:
1) X, Æ Î {F};
2) пересечение любой совокупности множеств из {F} принадлежит {F};
3) объединение любого конечного числа множеств из {F} принадлежит {F}.
Эти свойства полностью характеризуют замкнутые множества топологического пространства (X, t), а следовательно, и топологию t (так как множества из t – это дополнения замкнутых множеств) и могут быть приняты в качестве аксиом топологического пространства. Таким образом, топологию на Х можно задать, указав совокупность {F} подмножеств X, удовлетворяющую свойствам 1) – 3); в этом случае топологией на Х будет совокупность {X\F}.
Различные топологии на одном и том же множестве образуют частично упорядоченное множество.
Определение 2. Говорят, что топология t на Х слабее топологии t' на Х (t £ t'), если из того, что U Î t, следует, что U Î t', т. е. если t Ì t'. Топология t' в этом случае сильнее топологии t.
Заметим, что для всякой топологии t имеем tmin £ t £ tmax.
Очень часто получить описание всей топологии, как совокупности некоторых подмножеств Х, затруднительно. Для задания топологии используют построение совокупности подмножеств, порождающих топологию.
Определение 3. Совокупность Â = {V} открытых множеств топологического пространства (Х, t) называется базой топологии t, если для всякого открытого множества U Î t и для всякой точки х Î U найдется такое множество V Î Â, что х Î V и V Ì U.
Следовательно, всякое непустое открытое множество топологического пространства (Х, t) можно представить в виде объединения открытых множеств из базы топологии t (это свойство характеризует базу и часто принимается за определение базы). Достаточно взять объединение всех открытых множеств из базы, которые вложены в это множество.
Пусть {Va} – некоторая совокупность подмножеств Х. Возникает вопрос: при каких условиях можно построить топологию на Х так, чтобы семейство {Va} было базой этой топологии?
Теорема 1 (критерий базы). Пусть {Va}aÎА – некоторая не пустая совокупность подмножеств Х. Тогда Â = {Va}aÎА является базой некоторой топологии на Х, если
1) Х = 
 ,
,
2) для каждого Va и каждого Vb из Â и каждого x Î Va Ç Vb существует Vg Î Â такое, что х Î Vg Ì Va Ç Vb.
Доказательство. Если Â = {Va}aÎА – база топологии , то Va Ç Vb – открытое множество, и по определению базы для каждого x Î Va Ç Vb существует Vg Î Â такое, что х Î Vg Ì Va Ç Vb.
Обратно: если Â = {Va}aÎА удовлетворяет условию теоремы. Будем говорить, что множество U Ît, если U = 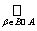
 Vb. Принадлежность Х Î t вытекает из условия 1). Принадлежность Æ Î t является следствием множественного равенства
Vb. Принадлежность Х Î t вытекает из условия 1). Принадлежность Æ Î t является следствием множественного равенства 
 Vb = Æ. Вторая аксиома проверяется непосредственно:
Vb = Æ. Вторая аксиома проверяется непосредственно: 
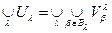 , т.е. объединение множеств из t представимо в виде объединения множеств из Â и, следовательно, также принадлежит t. Проверим третью аксиому. Для этого возьмем произвольные два множества U1, U2 Î t. Согласно определению системы t справедливы представления U1 =
, т.е. объединение множеств из t представимо в виде объединения множеств из Â и, следовательно, также принадлежит t. Проверим третью аксиому. Для этого возьмем произвольные два множества U1, U2 Î t. Согласно определению системы t справедливы представления U1 = 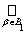
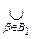 Vb, U2 =
Vb, U2 = 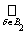
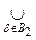 Vd. Тогда
Vd. Тогда
U1ÇU2 = ( 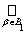
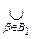 Vb)Ç(
Vb)Ç( 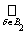
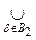 Vd) =
Vd) = 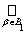
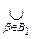
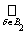
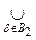 ( VbÇ Vd).
( VbÇ Vd).
Для доказательства нам достаточно показать, что множество VbÇ Vd = 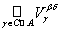
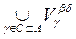 , где
, где 
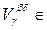 Â. Тогда U1ÇU2 =
Â. Тогда U1ÇU2 = 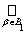
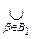
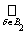
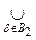
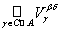
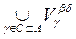 , т.е. объединение множеств из Â, а следовательно U1ÇU2 из t. В качестве системы множеств
, т.е. объединение множеств из Â, а следовательно U1ÇU2 из t. В качестве системы множеств 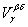
 в доказываемом равенстве берем все множества из Â, удовлетворяющие условию
в доказываемом равенстве берем все множества из Â, удовлетворяющие условию 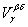
 Ì VbÇ Vd. Об этом говорит сайт https://intellect.icu . Тогда включение
Ì VbÇ Vd. Об этом говорит сайт https://intellect.icu . Тогда включение 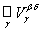
 Ì VbÇ Vd очевидно. Докажем обратное включение. Возьмем произвольное х Î VbÇ Vd. По определению системы Â найдется
Ì VbÇ Vd очевидно. Докажем обратное включение. Возьмем произвольное х Î VbÇ Vd. По определению системы Â найдется 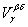
 Î Â такой, что х Î
Î Â такой, что х Î 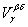
 Ì VbÇ Vd. Это означает, что х Î
Ì VbÇ Vd. Это означает, что х Î 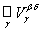
 и справедливо включение VabÇ Vad Ì
и справедливо включение VabÇ Vad Ì 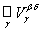
 .
.
Заметим, что в доказательстве мы указали и способ построения топологии, если задано семейство Â = {Va}aÎА, удовлетворяющее условию теоремы.
Пример 5. Пусть Х = Rn есть n-мерное векторное пространство. В качестве базы топологии на Rn можно взять систему множеств Â = {Va, b }, где Va, b = {х Î Rn: аi < xi < bi, i = 1, ..., n}, xi – координата вектора х = (x1, x2,…, xn); а = (а1, a2,…, аn), b = (b1, b2,..., bn) – произвольные векторы в Rn, причем аi < bi.
Такие множества Va, b называются открытыми параллелепипедами в Rn.
В дальнейшем, если не будет указано, какая именно топология рассматривается на Rn, мы будем считать, что Rn снабжено топологией, база которой указана в примере 5.
В топологическом пространстве естественно выбирать базу топологии с возможно меньшим количеством элементов. Например, в R1 множества V = (t1, t2), где t1, t2 рациональные числа, образуют базу топологии из счетного числа элементов.
Связное двоеточие — двуточечное топологическое пространство.
Вещественная прямая является топологическим пространством, если, например, назвать открытыми множествами произвольные (пустые, конечные или бесконечные) объединения конечных или бесконечных интервалов. Множество всех конечных открытых интервалов
является базой этой топологии. Это — стандартная топология на прямой. Вообще же на множестве вещественных чисел можно ввести очень разнообразные топологии, например,
, прямая с «топологией стрелки», где открытые множества имеют вид
, или топология Зарисского, в которой любое замкнутое множество — это конечное множество точек.
Вообще, евклидовы пространства являются топологическими пространствами. Базой их стандартной топологии можно выбрать открытые шары или открытые кубы. Обобщая далее, всякое метрическое пространство является топологическим пространством, базу топологии которого составляют открытые шары. Таковы, например, изучаемые в функциональном анализе бесконечномерные пространства функций.
Множество непрерывных отображений топологического пространства
в топологическое пространство
является топологическим пространством относительно следующей топологии, которая называется компактно-открытой. Предбаза задается множествами
, состоящими из отображений, при которых образ компакта
в
лежит в открытом множестве
в
.
Произвольное множество можно сделать топологическим пространством, если называть открытыми все его подмножества. Такая топология называется дискретной. В ней любые множества являются открытыми. Другой предельный случай — назвать открытыми минимально возможное количество подмножеств
, а именно, ввести тривиальную топологию — в ней открытыми являются лишь пустое множество и само пространство
.
Не всегда удобно перечислять все открытые множества. Часто удобнее указать некоторый меньший набор открытых множеств, который порождает их все. Формализацией этого является понятие базы топологии. Подмножество топологии называется базой топологии, если всякое открытое множество представляется как объединение множеств из
, то есть
Еще более экономный способ задания топологии состоит в задании ее предбазы — множества, которое становится базой, если к нему прибавить произвольные конечные пересечения его элементов. Для того, чтобы систему множеств можно было объявить предбазой топологии, необходимо и достаточно, чтобы она покрывала все множество
.
Наиболее часто предбазы используются для задания топологии, индуцированной на семейством отображений (см. далее).
Пусть — произвольное отображение множества
в топологическое пространство
. Индуцированная топология дает естественный способ введения топологии на
: за открытые множества в
берутся всевозможные прообразы открытых множеств в
; то есть
открыто, если существует открытое
такое, что
. Топология на
, описанная выше, является минимальной и единственной (по включению) топологией, в которой данное отображение является непрерывным.
Пример. Пусть топологическое пространство,
его подмножество. Если применить описанную выше конструкцию к теоретико-множественному вложению
, то получим топологию на подмножестве, обычно называемую также индуцированной.
Пусть — топологическое пространство, пусть также на нем задано некоторое отношение эквивалентности
, в таком случае есть естественный способ задать топологию на фактормножестве
. Мы объявляем подмножество фактора открытым тогда и только тогда, когда его прообраз при отображении факторизации является открытым в
. Легко проверить, во-первых, что это действительно определяет топологию, во-вторых, что это максимальная и единственная (по включению) топология, в которой указанное отображение факторизации непрерывно. Такая топология обычно называется фактортопологией на
.
Множество называется замкнутым, если его дополнение
— открытое множество. Задать топологию на
системой замкнутых множеств — значит предъявить систему
подмножеств
со свойствами:
Если система множеств с такими свойствами задана, с помощью операции дополнения строится система открытых множеств, задающая топологию на
.
В алгебраической геометрии применяется задание топологии на спектре (системе всех простых идеалов) коммутативного кольца с единицей —
. Топология на
вводится с помощью системы замкнутых множеств: пусть
— произвольный идеал кольца
(не обязательно простой), тогда ему соответствует множество
Все множества такого вида образуют систему множеств, удовлетворяющую перечисленным аксиомам, так как
Топология Зарисского в пространстве также задается с помощью системы замкнутых множеств. Замкнутыми множествами в топологии Зарисского принимаются все множества, являющиеся множеством общих нулей конечной системы многочленов. Выполнение аксиом системы замкнутых множеств следует из нетеровости кольца многочленов
и того факта, что общие нули произвольной системы многочленов совпадают с общими нулями идеала, который они образуют.
Пространство естественно вложено в спектр кольца многочленов
(оно совпадает с множеством всех его замкнутых точек), и топология Зарисского на
совпадает с той, что индуцирована топологией пространства
.
Понятие топологии является минимально необходимым для того, чтобы говорить о непрерывных отображениях. Интуитивно непрерывность есть отсутствие разрывов, то есть близкие точки при непрерывном отображении должны переходить в близкие. Оказывается, для определения понятия близости точек можно обойтись без понятия расстояния. Именно это и есть топологическое определение непрерывного отображения.
Отображение топологических пространств называется непрерывным, если прообраз всякого открытого множества открыт.
Категория топологических пространств в качестве объектов содержит все топологические пространства, а морфизмы — непрерывные отображения. Попыткам классифицировать объекты этой категории при помощи алгебраических инвариантов посвящен раздел математической науки, который называется алгебраической топологией. Изучению понятий непрерывности, а также других понятий, таких как компактность или отделимость, как таковых, без обращения к другим инструментам, посвящена общая топология. В качестве дополнительных структур на объекте
могут быть, например, пучок множеств на
или афинная прямая на
, то есть
. Обозначим категорию пространств из
с дополнительной структурой через
. Забывающий функтор
— декартовы расслоения. Объекты
называются пространствами со структурой. Объект слоя
над
называется структурой над
.
По Хохшильду функциональная структура на — отображение
, ставящее в соответствие каждому открытому множеству
подалгебру
алгебры непрерывных вещественнозначных функций на
. Это отображение является пучком алгебр — подпучком ростков непрерывных вещественнозначных функций на
, который содержит постоянный пучок. Это следует из условий, накладываемых на
:
Например, -многообразие с краем является паракомпактным хаусдорфовым пространством, наделенным функциональной структурой,
, локально изоморфным пространству
. Край состоит из тех точек, которые переводятся картами в точки гиперплоскости, являясь гладким
-мерным многообразием с индуцированной структурой.
Гомотопические группы сфер являются базовыми топологическими инвариантами, понимание которых приводит к лучшему пониманию топологических пространств в целом, так и наличие большого числа сложных закономерностей в их структуре.
Исследование, описанное в статье про топология, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое топология, топологическое пространство, база топологии и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ
Комментарии
Оставить комментарий
Функциональный анализ
Термины: Функциональный анализ