4. Понятие метрического пространства и топологии, определяемой метрикой. Примеры метрических пространств кратко

Привет, Вы узнаете о том , что такое 4. Понятие метрического пространства и топологии, определяемой метрикой. Примеры метрических пространств, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 4. Понятие метрического пространства и топологии, определяемой метрикой. Примеры метрических пространств , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Определение 7. Метрическим пространством называется пара (Х, d), где Х - произвольное множество, а d: X´X ® R - отображение, называемое метрикой, удовлетворяет следующим трем аксиомам:

1. d(x, y) ³ 0; d(x, y) = 0 Û x = y (неотрицательность).

2. d(x, y) = d(y, x) (симметричность).

3. d(x, y) £ d(x, z) + d(z, y) (неравенство треугольника).

Пример 6. Евклидово пространство Rn состоит из множества всех n-мерных векторов, метрика в котором задается равенством d(x, y) = 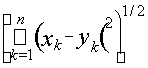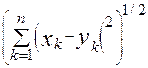. Справедливость аксиом метрики (за исключением неравенства треугольника) очевидна. Неравенство треугольника вытекает из неравенства Минковского для сумм (см. приложение). Введенная таким образом метрика на Rn называется евклидовой.

Пример 7. В пространстве непрерывных функций C[a, b] на отрезке [a, b] введем метрику d(x, y) = max |x(t) – y(t)|, где максимум берется по t Î[a, b]. Эта метрика называется метрикой Чебышева. Справедливость аксиом метрики практически очевидна.

Пример 8. Сk[a, b] – метрическое пространство всех непрерывных функций на [a, b], имеющих непрерывные производные до порядка k, с метрикой, определенной по формуле

d(x, y)= .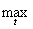

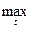
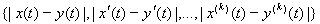
Справедливость аксиом метрики очевидна.

Пример 9. Об этом говорит сайт https://intellect.icu . M[a, b] – пространство ограниченных вещественных функций x(t) заданных на отрезке [a, b] с метрикой d(x, y) = 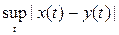. Ясно, что C[a, b] Ì M[a, b]. Справедливость аксиом метрики очевидна.

Пример 10. lp (1£ р < ¥) – пространство всех числовых последовательностей х = {xk}, для которых сходится ряд 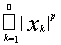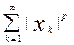. Метрика в этом случае определяется так:

d(x, y) = < ¥.

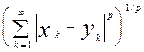Выполнение двух первых аксиом очевидно. Неравенство треугольника вытекает из неравенства Минковского (см. приложение).

Пример 11. l¥ = m - пространство ограниченных числовых последовательностей с метрикой

d(х, у) = sup|xk - yk|

Справедливость аксиом метрики очевидна.

Пример 12. с0 - пространство сходящихся к нулю последовательностей с той же метрикой, что и в m.

Пример 13. Для произвольного множества Х определим метрику

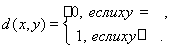
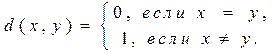
Справедливость аксиом метрики очевидна. Рассмотренное пространство называется дискретным метрическим пространством.

Пример 14. s - пространство всех числовых последовательностей. Введем в s метрику соотношением:

Аксиомы 1 и 2 метрики очевидны , выполнение 3 аксиомы следует из возрастания функции t/(1+t) (проверьте!).

Определение 8. Обозначим через S(x0, r) = {x: d(x0,x) < r } - открытый шар, S[x0, r] = {x: d(x0,x) £ r} - замкнутый шар.

Пример 15. Пусть Х = R3 – трехмерное евклидово пространство. Шар S(a, r) – это обычный шар радиуса r с центром в а = (а1, а2, а3).

Пример 16. Пусть Х = С[а, b] , тогда шар (a, r) в пространстве С[а, b] – это совокупность функций x(t) графики которых не выходят из полосы шириной 2r, образованной кривыми x0(t) – r и x0(t) + r (рис.). Определение 9 (топология метрического пространства). Определим базу топологии Â в метрическом пространстве (X, d) полагая, что Â = {S(x, r): "r > 0, " x Î X}. Очевидно, что данное семейство удовлетворяет условиям теоремы 1 и порождает топологию в метрическом пространстве.

Отметим следующее свойство расстояний, которые можно называть “неравенством четырехугольника”: для любых четырех точек x, y, z, u метрического пространства

|d(x, y) - d(z, u)| £ d(x, z) + d(y, u).

Геометрически это означает, что разность двух сторон четырехугольника не превосходит суммы двух других сторон.

Доказательство вытекает из неравенств

d(x, y) £ d(x, z)+d(z, u)+d(u, y),

d(z, u) £ d(z, x)+d(x, y)+d(y, u),

если из первого вычесть d(z, u), а из второго d(x, y). При y = u неравенство четырехугольника обращается во второе неравенство треугольника

|d(x, y) - d(y, z)| £ d(x, z),

которое также часто применяется.

Исследование, описанное в статье про 4. Понятие метрического пространства и топологии, определяемой метрикой. Примеры метрических пространств, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 4. Понятие метрического пространства и топологии, определяемой метрикой. Примеры метрических пространств и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ

Из статьи мы узнали кратко, но содержательно про