Привет, Вы узнаете о том , что такое 10. Компактные пространства, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 10. Компактные пространства , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Вначале обсудим некоторые понятия, связанные с покрытиями топологических пространств. Пусть r = {А} – некоторая система подмножеств А множества Х. Объединение всех А из r обозначим `r и назовем телом системы r.

Определение 22. Система r называется покрытием подпространства Х топологического пространства Y, если `r É Х .

Определение 23. Говорят, что покрытие r подпространства Х является подпокрытием покрытия r' подпространства Х, если каждый элемент r является элементом системы r'.

Отношение подпокрытие вводит частичную упорядоченность в множестве всех покрытий подпространства Х. Покрытия, состоящие из конечного или счетного числа элементов, называются соответственно конечными или счетными.

Особое значение имеют покрытия, состоящие из открытых множеств. Такие покрытия называются открытыми.

Со свойствами открытых покрытий связаны многие важные свойства пространства. В связи с этим выделяют следующие классы пространства.

Определение 24. Пусть Y - топологическое пространство. Множество Х Ì Y называется компактным, если для всякого его открытого покрытия существует конечное открытое подпокрытие.

В этом случае говорят, что любое открытое покрытие содержит конечное подпокрытие.

Компактное множество Х с индуцированной топологией является топологическим пространством. Его называют компактным пространством.

Пример 18. Пусть Х = [а, b] – из R1. Множество Х компактно, так как по теореме Гейне – Бореля из любого покрытия Х интервалами можно выделить конечное подпокрытие.

Теорема 13. Всякое замкнутое подмножество X компактного пространства Y само компактно.

Доказательство. Пусть r = {A} - открытое покрытие Х. Тогда, по определению индуцируемой топологии, для любого множества А из покрытия r справедливо предстваление А = ВÇ Х , где В – открытые множества из Y. В силу замкнутости Х, множество Y\X является открытым и система множеств {B}È{Y\X} образует открытое покрытие Y. Так как Y компактно, из этого покрытия можно выделить конеченое подпокрытие, которое содержит множества В1, В2, …, Вn и, возможно, множество Y\X. Следовательно, Y = 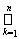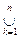Вk È( Y\X). Но тогда множества Аk = ВkÇХ, k = 1, 2, …, n, являются конечным открытым покрытием для Х. Последнее означает, что Х компактное множество.

Следующая теорема часто применяется в анализе.

Теорема l4. Всякое бесконечное множество Z Ì Х компактного множества Х имеет в Х предельную точку.

Доказательство. Предположим противное, т. е. что Z' = Æ. Тогда `Z = Z, значит, Z замкнуто, а следовательно, и компактно. С другой стороны, каждая точка z Î Z не является по предположению предельной. Тогда существует открытая окрестность О(z) в Х с условием О(z)ÇZ = {z}. Такие окрестности О(z) образуют бесконечное покрытие пространства Z, из которого нельзя выбрать конечное подпокрытие в противоречии с компактностью Z.

Понятие компактности тесно связано с понятием замкнутости, как показывает следующее утверждение.

Теорема 15. Пусть Х – компактное подножество хаусдорфова пространства Y. Тогда Х замкнуто.

Доказательство. Пусть у Î Y\Х. Для любой точки х Î Х в силу хаусдорфовости Y найдутся такие открытые окрестности Ux(y), Vy (х) точек у, х, что Ux(у) Ç Vy (х) = Æ.

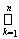
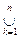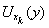
Система (Vy(х))x Î X образует открытое покрытие Х. В силу компактности Х имеется конечное подпокрытие (Vy(хk))k=1n . Легко видеть, что множества V(X) = Vy(хk) и U(у) = 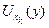открыты и не пересекаются. Об этом говорит сайт https://intellect.icu . Таким образом, показано, что в хаусдорфовом пространстве компактное множество Х и точку, не лежащую в нем, можно разделить непересекающимися окрестностями U(х) и U(y). Отсюда следует, что дополнение Y\Х открыто, поэтому Х замкнуто.

Задачи

1. Что представляет собой шар S(0, 1) m с центром в точке 0 = (0,0, 0, …) и радиуса 1.

2. Пусть l1 – множество элементов x вида x = { 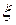i}, где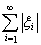 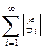< 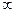, с расстоянием

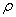
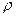(x, y) =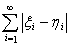 , где y={ }.

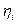Доказать, что l1 - метрическое пространство. Что представляет собой шар S(0, 1) в этом пространстве?

3. Показать, что если множество Е на прямой покрыто произвольной системой интервалов, то из нее можно выделить (не более чем счетную) подсистему, также покрывающую Е.

4. Показать, что если множество Е на плоскости покрыто произвольной системой кругов, то из нее можно выделить не более чем счетную подсистему, также перекрывающую Е.

5. Обозначим множество предельных точек любого множества А через А′. Построить на прямой множество А так, чтобы А″=( А′)′ было не пустым, а А′″ – пустым.

6. Доказать, что множество А′ (см. задачу 5) замкнуто, каково бы ни было А.

7. Известно, что А′ счетно. Доказать, что А счетно (А – на прямой).

8. Точка x на прямой называется точкой конденсации несчетного множества А, если в любой окрестности точки x имеется несчетное множество точек множества А. Доказать, что у всякого несчетного множества А имеются точки конденсации.

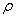
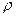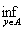
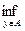
9. Величина (x,A)= 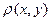называется расстоянием от точки x до множества А. Доказать, что для замкнутого множества А соотношение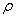 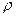(x,A)=0 и x 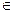А, эквивалентны; если же А не замкнуто, то они не эквивалентны.

10. Доказать, что для любого множества А совокупность точек х, для которых 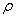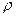(x,A)<ε, открыта, а совокупность точек y, для которых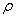 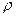(x,A) 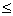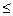ε, замкнута.

11. Непосредственно из определения замкнутого множества вывести, что любое конечное множество точек метрического пространства замкнуто.

12. Доказать, что (AÈB)′=A′ÈB′.

13. Следует ли из 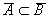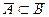, что A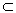 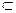B?

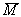
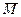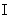
14. Доказать, что = 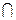F, где F – всевозможные замкнутые множества, содержащие M.

15. В пространстве С[a, b] множество Mn есть совокупность всех полиномов степени, не превышающей n. Что представляет собой ?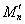

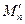16. Доказать включение 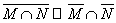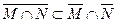. Можно ли знак включения заменить знаком равенства?

17. Обозначим через 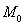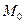множество всех внутренних точек множества. Доказать, что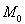 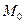открыто.

18. Пусть М множество точек 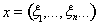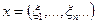пространства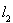 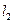, у которых все координаты положительны. Будет ли М открыто?

19. Пусть 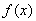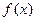функция, определенная и непрерывная на всей числовой оси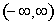 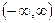. Доказать, что множество точек x,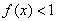 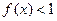открыто.

20. В пространстве множество A состоит из функций 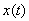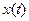, значение которых при любом t принадлежит заданному замкнутому множеству M вещественных чисел. Будет ли A замкнуто? Будет ли A открыто, если M открыто?

21. Доказать, что множество всех изолированных точек сепарабельного метрического пространства не более чем счетно.

22. Показать, что если F - замкнутое множество, то 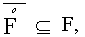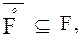но, вообще говоря (показать на примере), равенства здесь может и не быть (нуликом обозначена внутренность).

23. Верно ли утверждение: внутренняя часть пересечения двух множеств равна пересечению их внутренних частей. Верно ли аналогичное утверждение для объединений двух множеств.

24. Доказать, что граница каждого множества замкнута.

25. Построить на числовой прямой множество, обладающее следующими тремя свойствами: 1) все его точки изолированые; 2) точная нижняя грань расстояний между различными точками равна нулю; 3) оно не имеет предельных точек.

26. Пусть Ф – дважды непрерывно дифференцируемая на [0, ¥) функция, которая удовлетворяет следующим условиям: а) Ф(0) = 0; Ф(х) > 0 при х > 0; б) Ф¢(х) ³ 0 и Ф¢¢(х) £ 0 при х ³ 0. Доказать, что функция r(х, у) = Ф(|x – y|) определячет метрику на R.

Исследование, описанное в статье про 10. Компактные пространства, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 10. Компактные пространства и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ