3. Структура открытых множеств и окрестности кратко

Привет, Вы узнаете о том , что такое 3. Структура открытых множеств и окрестности, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 3. Структура открытых множеств и окрестности , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Пусть (Х, t) – топологическое пространство и х Î Х – произвольная точка.

Определение 4. Окрестностью точки х Î Х называется всякое подмножество U(х) Ì Х, удовлетворяющее условиям:

1) х Î U(х);

2) существует V Î t такое, что х Î V Ì U(х).

Отметим, что в силу этого определения любое открытое множество является окрестностью каждой своей точки. Окрестность точки, которая является открытым множеством, называется открытой окрестностью.

Можно рассматривать совокупность всех окрестностей данной точки х. Эта совокупность обладает следующими свойствами (докажите!):

1) всякое множество, содержащее некоторую окрестность точки х, является окрестностью точки х;

2) пересечение конечного числа окрестностей точки х – окрестность точки х;

3) объединение любой совокупности окрестностей точки х есть окрестность тачки х.

Теорема 2. Подмножество А (А ¹ Æ) топологического пространства (Х, t) открыто тогда и только тогда, когда оно содержит некоторую окрестность каждой своей точки.

Доказательство. Пусть А открыто, х Î А. Тогда ясно, что А – окрестность х, следовательно, А содержит окрестность любой своей точки.

Пусть для каждого х Î А существует окрестность U точки х, целиком лежащая в А: U Ì A. По определению окрестности в ней содержится некоторое открытое множество Vх, х Î Vх Ì U Ì A. Рассмотрим объединение 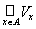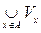вcex таких множеств. Оно открыто и совпадает с А. Действительно, так как всякая точка множества А принадлежит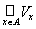 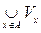, то А Ì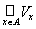 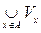. Об этом говорит сайт https://intellect.icu . С другой стороны, для каждого х имеем Vx Ì А, т. е.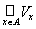 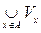Ì А. Поэтому А =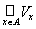 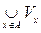значит, А открыто.

Теорема 3. Множество А Ì R1 открыто тогда и только тогда, когда представимо в виде 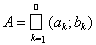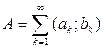(напомним, что под суммой множеств понимается их объединение, при условии, что эти множества не пересекаются друг с другом).

Доказательство. Достаточность утверждения очевидна, установим необходимость. На множестве А введем отношение х ~ у, если существует интервал (a; b) Ì А, содержащий обе эти точки. Данное отношение является эквивалентностью. Первые два условия в определении эквивалентности проверяются просто. Последнее вытекает, что если два интервала принадлежат А и имеют общую точку, то их объединение также будет интервалом, причем принадлежащим А.

В результате множество А этим отношением эквивалентности разбивается на непересекаемые классы эквивалентности. Рассмотрим один такой класс [x] и пусть 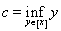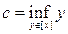и 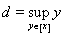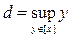. Так как множество А открытое, то любая точка этого множества является внутренней, т.е. входит в А с некоторым интервало. Поэтому всегда c < d. Может случится, что эти числа бесконечности. В этом случае рассуждения более простые. Пусть - ¥ < c < d < +¥. Докажем, что (c; d) Ì A. Действительно, пусть s Î (c; d). В силу свойств точных граней и числовых множеств найдутся у и z из [x], такие, что c < y < s < z < d. Так как у ~ z, то существует интервал (r; q) Ì A и такой, что y, z Î (r; q). Но тогда и s Î (r; q) Ì А и этим доказано, что (c; d) Ì A. Заметим, что одновременно мы практически показали принадлежность s Î [x]. Это означает, что (c; d) Ì [x]. Так как обратное вложение очевидно из определения c и d, то [x] = (c; d).

Последнее равенство завершает доказательство теоремы, так как таких интервалов, содержащихся в А, не может быть более чем счетное число. Действительно, в каждом интервале достаточно взять рациональное число. Разным интервалам будут соответствовать разные числа и количество интервалов биективно отображается в некоторое подмножество множества рациональных чисел. Последнее, как подмножество счетного множества, обязано быть не более чем счетным.

Следствие. Всякое замкнутое множество на прямой получается из прямой выбрасыванием конечного или счетного числа интервалов.

Окрестности используют для отделения точек друг от друга.

Определение 5. Топологическое пространство (Х, t) называется хаусдорфовым или отделимым, если для любых двух его различных точек, х, у, найдутся такие окрестности V(х), V(у) этих точек, что V(х) Ç V(у) = Æ.

Топологическое пространство (Х, t) с тривиальной топологией не является хаусдорфовым, если оно содержит более одной точки (проверьте!).

Свойства окрестностей точки, рассмотренные выше, можно положить в основу следующего определения топологического пространства, объявляя их аксиомами.

Определение 6. Топологическое пространство – это множество Х, для каждой точки х которого указана непустая система подмножеств {О(х)}, называемых окрестностями точки х, удовлетворяющих следующим свойствам:

1) х принадлежит каждой своей окрестности О(x);

2) если множество U Ì Х содержит некоторое О(х), то U – также окрестность точки х;

3) для любых окрестностей O1(х), O2 (х) точки х их пересечение O1(х) Ç O2 (х) также является окрестностью точки х;

4) для всякой окрестности O(x) точки х найдется такая окрестность O1 (х) Ì O(х), которая является окрестностью каждой своей точки.

Исследование, описанное в статье про 3. Структура открытых множеств и окрестности, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 3. Структура открытых множеств и окрестности и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ