Лекция
Привет, Вы узнаете о том , что такое 9. Нигде не плотные множества. Понятие категории множеств метрического пространства. Теорема Бэра, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 9. Нигде не плотные множества. Понятие категории множеств метрического пространства. Теорема Бэра , настоятельно рекомендую прочитать все из категории Функциональный анализ.
Определение 15. Пусть Х – метрическое пространство Множество А Ì Х называется нигде не плотным, если его замыкание `А не имеет внутренних точек. Последнее эквивалентно тому, что в любом шаре найдется шар, не содержащий точек из `А.
Действительно, возьмем любой шар S. Он не может лежать полностью в множестве `А, т.к. в этом случае все его внутренние точки окажутся внутренними для `А. Следовательно, SÇ(X - `А) ¹ Æ. Тогда для любой точки х Î SÇ(X - `А) (множество Х - `А – открыто) найдется шар малого радиуса S1, который полностью лежит в SÇ(X - `А), а следовательно не имеет общих точек с `А. Обратное очевидно.
Определение 16. Счетное объединение нигде не плотных множеств называется множеством первой категории, а множество, не являющееся множеством первой категории, - множеством второй категории.
Теорема 17 (Бэра). Полное метрическое пространство является множеством второй категории, т.е. не может быть объединением счетного множества нигде не плотных множеств.
Доказательство. Предположим противное, что полное метрическое пространство X является счетным объединением нигде не плотных в X множеств X = 
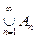 . Рассмотрим непустое открытое множество X – `А1 и некоторую точку x1 из этого множества. Найдется открытый шар S(xl, r1), который содержится в множестве X – `А1. Для этого шара справедливы соотношения S(x1, r1/2) Ì S[x1, r1/2] Ì S(x1, r1). Следовательно, S[x1, r1/2] Ç`А1 = Æ.
. Рассмотрим непустое открытое множество X – `А1 и некоторую точку x1 из этого множества. Найдется открытый шар S(xl, r1), который содержится в множестве X – `А1. Для этого шара справедливы соотношения S(x1, r1/2) Ì S[x1, r1/2] Ì S(x1, r1). Следовательно, S[x1, r1/2] Ç`А1 = Æ.
Возьмем точку х2 из непустого открытого множества S(x1, r1/2)Ç (X – `А2) (см. рассуждения после определения 15). Найдется открытый шар S(х2, r2), содержащийся в этом пересечении. Не умаляя общности, можно считать, что r2 £ r1/2, т.е. можно уменьшить радиус шара, не нарушая включения
S(х2, r2) Ì S(x1, r1/2)Ç (X – `А2).
Тогда справедливы включения
S(х2, r2/2) Ì S[х2, r2/2] Ì S(х2, r2) Ì S(x1, r1/2)Ì S[x1, r1/2],
причем S[x2, r2/2] Ç`А2 = Æ.
Далее, по индукции, в непустом открытом множестве
S(xn - 1, rn - 1/2)Ç (X – `Аn)
найдется открытый шар S(хn, rn), rn £ rn – 1/2, для которого выполняются включения
S(хn, rn/2) Ì S[хn, rn/2] Ì S(хn, rn) Ì S(xn - 1, rn - 1/2)Ì S[xn - 1, rn - 1/2],
причем S[xn, rn/2] Ç`Аn = Æ.
Мы построили последовательность { S[xn, rn/2]} замкнутых вложенных шаров с радиусами rn/2 £ rn – 1/22 £ … £ r1/2n, стремящимися к нулю при n ® ¥, для которых S[xn, rn/2] Ç`Аn = Æ. По критерию полноты метрических пространств существует точка х, принадлежащая всем шарам. Из равенства X = 
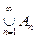 следует, что х принадлежит какому-то из множеств, скажем Am.. Мы получили противоречие: x Î S[xm, rm/2] ÇАm, в тоже время по построению шаров S[xm, rm/2] Ç`Аm = Æ и тем более S[xm, rm/2] ÇАm = Æ.
следует, что х принадлежит какому-то из множеств, скажем Am.. Мы получили противоречие: x Î S[xm, rm/2] ÇАm, в тоже время по построению шаров S[xm, rm/2] Ç`Аm = Æ и тем более S[xm, rm/2] ÇАm = Æ.
Следствие. Если полное метрическое пространство X является счетным объединением замкнутых множеств, то хотя бы одно из них содержит шар положительного радиуса.
1. Пусть M нигде не плотное множество метрического пространства. Каким будет его дополнение?
2. Пусть X – пространство элементов вида 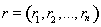
 , где n – фиксировано,
, где n – фиксировано, 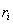
 - рациональные числа, с метрикой
- рациональные числа, с метрикой

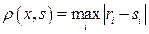
Будет ли это пространство полным? Что будет являться его пополнением?
3. Об этом говорит сайт https://intellect.icu . В пространстве 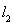
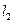 построить последовательность вложенных друг в друга замкнутых множеств с пустым пересечением.
построить последовательность вложенных друг в друга замкнутых множеств с пустым пересечением.
4. Показать, что пространство 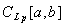
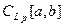 непрерывных функций с метрикой
непрерывных функций с метрикой
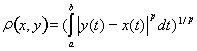

неполно ни при каком p.
5. Ввести на прямой 
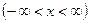 метрику по формуле
метрику по формуле

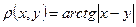
Проверить выполнение всех аксиом метрического пространства. Будет ли это пространство полным?
6. Доказать, что пространство Сm[a, b] полно при любом m.
7. Является ли полным пространство всех числовых последовательностей
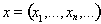
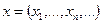
где 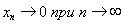
 , с метрикой по формуле
, с метрикой по формуле
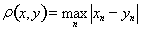
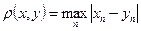 ?
?
8. Рассмотрим три пространства функций на прямой с метрикой d(f(x), g(x)) = 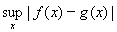
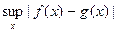 :
:
а) всех ограниченных непрерывных функций;
б) всех непрерывных функций, у которых 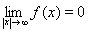
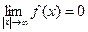 ;
;
в) всех непрерывных функций, каждая из которых равна нулю вне некоторого интервала.
Будут ли указанные пространства полными?
9. Отображение A на полупрямой 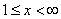
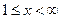 переводит точку x в
переводит точку x в 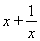
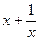 . Является ли отображение сжимающим? Имеет ли неподвижную точку?
. Является ли отображение сжимающим? Имеет ли неподвижную точку?
10. Пусть функция 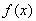
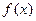 , заданная и дифференцируемая на отрезке [0, 1], удовлетворяет неравенствам
, заданная и дифференцируемая на отрезке [0, 1], удовлетворяет неравенствам


Будет ли уравнение 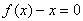
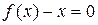 иметь решение?
иметь решение?
11. В пространстве 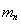
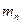 элементов вида
элементов вида 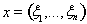
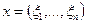 с метрикой
с метрикой 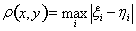
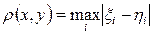 . Найти условие разрешимости системы
. Найти условие разрешимости системы


12. Непрерывны ли функции 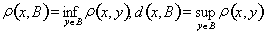
 , где B – множество в метрическом пространстве X.
, где B – множество в метрическом пространстве X.
13. Дано отображение компакта в себя, удовлетворяющее условию 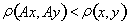
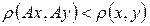 при
при 
 . Показать, что у этого отображения существует единственная неподвижная точка.
. Показать, что у этого отображения существует единственная неподвижная точка.
14. Может ли компактное множество быть неограниченным?
15. Привести пример компактного в пространстве m множества, все точки которого имеют бесконечное множество координат, отличных от нуля.
16. Будет ли компактным в пространстве C[a, b] множество всех степеней 
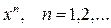 ?
?
17. Показать, что последовательность непрерывных функций 
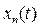 на отрезке [0, 1], где
на отрезке [0, 1], где
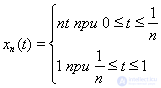

сходится по расстоянию к 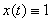
 и в
и в 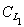
 и в
и в 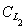
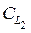 (см. задачу 4), но не стремящуюся в С[a, b] в метрике Чебышева (пример 7, гл. 1) к единице при t = 0.
(см. задачу 4), но не стремящуюся в С[a, b] в метрике Чебышева (пример 7, гл. 1) к единице при t = 0.
18. Пусть Х - метрическое пространство, в котором любая последовательность точек содержит фундаментальную подпоследовательность. Доказать, что пространство Х сепарабельно.
19. Показать, что пространств h всех числовых последовательностей, каждая из которых имеет лишь конечное число отличных от нуля членов, с метрикой d(x, y) = sup n |xn - yn| является неполным сепарабельным метрическим пространством. Каково пополнение этого пространства?
20. Показать, что пространство С(-¥, ¥) всех определенных на числовой прямой непрерывных функций, каждая из которых обращается в нуль вне некоторого интервала, с метрикой

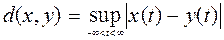
является неполным сепарабельным метрическим пространством. Каково пополнение этого пространства?
21. Показать, что множество F замкнуто тогда и только тогда, когда из d(x, F) = 0 следует хÎF.
22. В любом ли метрическом пространстве замыкание открытого шара S(x, r) совпадает с замкнутым шаром S[x, r]?
23. Обозначим АК множество всех функций из С[a, b], удовлетворяющих условию Липшица с одной и той же константой К:
|x(t) - x(s)| £ K|t - s|.
Показать, что множество АК совпадает с замыканием множества всех дифференцируемых на сегменте [a, b] функций x(t) таких, что |x¢(t)| £ K.
24. Указать в эвклидовой плоскости два таких замкнутых непересекающихся множества А и В, что d(А, В) = 1, но не существует точек аÎА и bÎВ таких, что d(а, b) = 1.
25. Показать, что если А - компактное, а В замкнутое множества в метрическом пространстве Х и АÇВ = Æ, то d(А, В) > 0.
26. Пусть f(х) - непрерывное взаимооднозначное отображение компактного метрического пространства Х на метрическое пространство У. Доказать, что обратное отображение f -1(у) пространства У на пространство Х непрерывно.
27. Доказать, что если возрастающая последовательность {xn(t)} вещественных непрерывных функций, заданных на компактном метрическом пространстве Х, поточечно сходится к непрерывной функции х(t), то она сходится к х(t) равномерно.
28. Пусть d(x, y) - метрика на Х. Показать, что
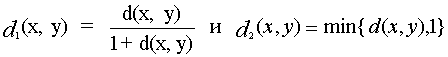
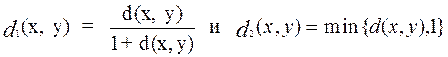
также является метрикой на Х и что эти три метрики попарно эквивалентны.
29. Пусть Х - метрическое пространство, в котором любая последовательность точек содержит фундаментальную подпоследовательность. Доказать, что пространство Х сепарабельно.
30. Показать, что пространств h всех числовых последовательностей, каждая из которых имеет лишь конечное число отличных от нуля членов, с метрикой d(x, y) = sup n |xn - yn| является неполным сепарабельным метрическим пространством. Каково пополнение этого пространства?
31. Пусть Х - метрическое пространство с метрикой
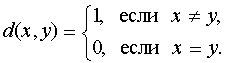
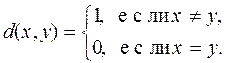
Ответить на следующие вопросы: 1) В каком случае {xn} будет сходящейся последовательностью в Х? 2) В каком случае {xn} будет фундаментальной последовательностью в Х? 3) Будет ли Х полным пространством? 4) Какие множества всюду плотны в Х? 5) В каком случае Х является сепарабельным пространством? 6) Какие множества в Х открыты, замкнуты?
32. В любом ли метрическом пространстве замыкание открытого шара S(x, r) совпадает с замкнутым шаром S[x, r]?
Исследование, описанное в статье про 9. Нигде не плотные множества. Понятие категории множеств метрического пространства. Теорема Бэра, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 9. Нигде не плотные множества. Понятие категории множеств метрического пространства. Теорема Бэра и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Функциональный анализ
Термины: Функциональный анализ