4. Резольвента и спектр оператора. Линейная независимость собственных векторов. Спектр вполне непрерывного оператора (конечномерность собственного подпространства, конечное число собственных значений вне круга) кратко

Привет, Вы узнаете о том , что такое 4. Резольвента и спектр оператора. Линейная независимость собственных векторов. Спектр вполне непрерывного оператора (конечномерность собственного подпространства, конечное число собственных значений вне круга), Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 4. Резольвента и спектр оператора. Линейная независимость собственных векторов. Спектр вполне непрерывного оператора (конечномерность собственного подпространства, конечное число собственных значений вне круга) , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Часто вместо уравнений (3) приходится рассматривать уравнения

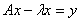
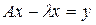(8)

где 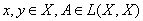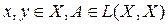, х – искомый, у – известный элемент, а l – некоторый числовой параметр. Уравнение (8) можно также записать в виде

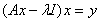
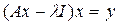(8*)

Одновременно с уравнением (8) целесообразно рассматривать уравнение

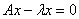
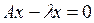(9)

которое, называют однородным уравнением, соответствующим уравнению (8). Уравнение же (8) называют тогда неоднород­ным. Ясно, что однородное уравнение всегда имеет нулевое решение x = 0.

Пусть оператор 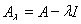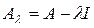для данного значения пара­метра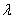 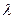имеет обратный оператор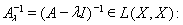 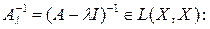этот оператор называют разрешающим оператором или резольвентой для уравнения (8) или оператора А и обо­значают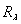 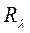. Тогда уравнение (8) при любом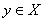 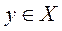имеет решение и притом только одно. Однородное уравнение (9) имеет в этом случае лишь нулевое решение. Такие значения параметра l называются регулярными значениями оператора А или уравнения (8). Множество значений параметра l, не являющиеся регулярными, называются спектром оператора А. Может случиться, что однородное уравнение (9), кроме нулевого, имеет еще одно или несколько ре­шений, отличных от нуля. Такие значения параметра, при которых это происходит, называются характеристическими числами или собственными значе­ниями оператора А. Так как в этом случае решение урав­нения (9), являющегося частным случаем уравнения (8), не однозначно, то собственные значения принадлежат спектру. Однако могут существовать точки спектра, не являющиеся собственными значениями.

В 7 главе (теорема 7) рассматривался вопрос обратимости оператора 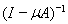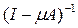. В этом случае обратный оператор не является, строго говоря, резольвентой оператора А. Однако с помощью этого оператора резольвенту можно по­лучить без труда. В самом деле, преобразуем оператор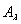 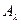следующим образом:

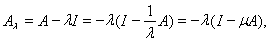
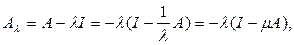
где 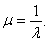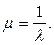Если теперь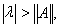 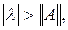то 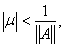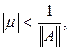и поэтому существует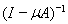 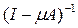. Но тогда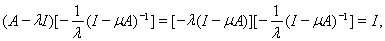 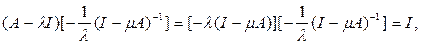т.е. 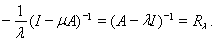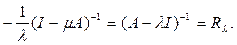Таким образом, резольвента представима в виде сходящегося в области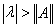 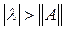ряда

=

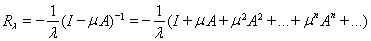
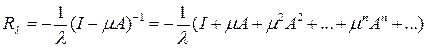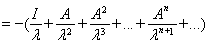
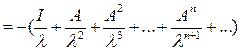
Пример 1. Рассмотрим в пространстве С [0, 1] опе­ратор умножения на независимое переменное 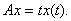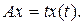Уравнение (8) принимает в этом случае

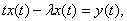
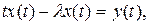(10)

и решение x(t) этого уравнения есть функция, тождественно ему удовлетворяющая. Об этом говорит сайт https://intellect.icu . Если 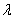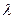лежит вне отрезка [0, 1], то уравнение (10) имеет при любом у (t) единственное непрерывное решение

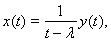
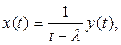
откуда следует, что все такие значения параметра 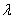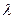являются регулярными, и резольвента есть оператор умножения на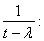

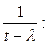
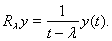
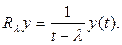
Все значения параметра, принадлежащие отрезку [0, 1], являются точками спектра. В самом деле, пусть 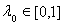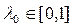. Возьмем в качестве y(t) какую-нибудь функцию, не обращающуюся в нуль в точке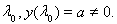 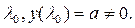Для такой функции равенство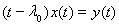 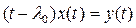не может тождественно удовлетворяться ни при какой непрерывной на отрезке [0, 1] функции х (t), ибо в точке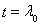 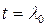левая часть его равна нулю, в то время как правая отлична от нуля. Следовательно, при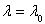 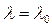уравнение (10) не имеет решения для произвольной правой части, что и доказывает принадлежность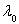 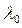спектру оператора А, Вместе с тем ни одна точка спектра не является собственным значением, так как решение однородного уравнения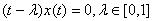 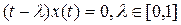при любом t, отличном от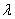 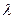, а следовательно, в силу непрерывности и при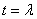 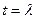обращается в нуль, т.е. тождественно равно нулю.

Пример 2. Положим Х = Y = Rn и пусть оператор А задается квадратной матрицей 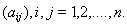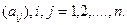Уравнение (4) примет для 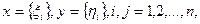вид

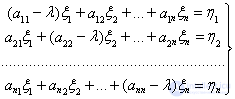
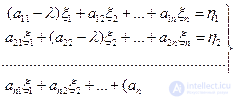(11)

Это есть система 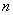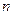линейных неоднородных алгебраических уравнений. Если определитель системы

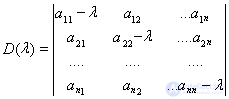
отличен от нуля, т. е. если 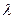не есть корень уравнения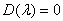 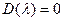, то система уравнений (11) имеет при любых правых частях единственное решение, и следовательно, все такие значения параметра l регулярны. Корни уравнения D(l) = 0 образуют спектр, так как при таких l система (11) в общем случае не­разрешима. Однако при этих значениях параметра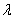 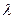однород­ная система

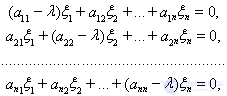
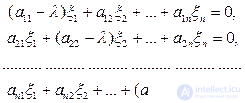
имеет нетривиальное решение (т. е. отличное от нулевого), и, следовательно, любая точка спектра есть собственное зна­чение.

В приведенных примерах спектр оператора либо не со­держал, ни одного собственного значения, либо состоял только, из собственных значений. Имеются примеры, где спектр оператора содержит как собственные значения, так и точки, не являющиеся собственными значениями.

Лемма 5. Собственные векторы симметрического оператора, отвечающие различным собственным значениям, взаимно ортогональны.

Доказательство. Действительно, пусть имеют место равенства

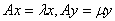
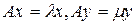и .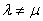

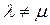Умножим первое равенство скалярно на 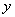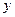, второе на 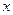и вычитая второе из первого, получим

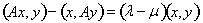
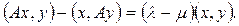
Левая часть равенства равна нулю вследствие симметрии оператора А. Так как 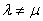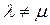, то 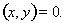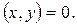Лемма 5 доказана.

Лемма 6. У вполне непрерывного оператора А всякая ортогональная нормированная система собственных векторов с собственными значениями, превосходящими по модулю положительное значение d, конечна.

Доказательство. Допустим, что нашлась бесконечная система 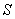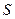таких собственных векторов. Каждый из них оператором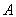 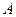переводится в себя самого с числовым множителем, по модулю большим числа d. Пусть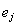 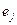и 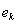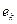- какие-то два из этих собственных векторов:

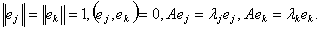
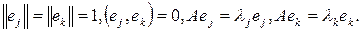
Имеем

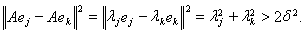
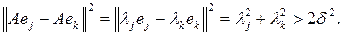
Это означает, что расстояние между векторами, полученными после воздействия оператора 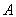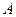на вектора системы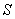 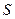, заведомо будут превосходить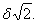 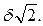Но из совокупности таких векторов нельзя выбрать никакой сходящейся последовательности, что противоречит полной непрерывности оператора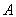 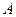. Лемма 6 доказана.

Следствие. Существует только конечное число взаимно ортогональных векторов с данным собственным значением 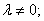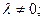иными словами, каждое собственное подпространство, отвечающее ненулевому собственному значению( т.е. совокупность всех собственных векторов оператора А с фиксированным собственным значением l. Это множество очевидно, есть (замкнутое) подпространство в Н) вполне непрерывного симметричного оператора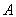 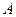конечномерно.

Исследование, описанное в статье про 4. Резольвента и спектр оператора. Линейная независимость собственных векторов. Спектр вполне непрерывного оператора (конечномерность собственного подпространства, конечное число собственных значений вне круга), подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 4. Резольвента и спектр оператора. Линейная независимость собственных векторов. Спектр вполне непрерывного оператора (конечномерность собственного подпространства, конечное число собственных значений вне круга) и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ