6. Сопряженный оператор. Условия существования сопряженного оператора. Замкнутость сопряженного оператора. Сопряженный оператор к ограниченному оператору и его норма. кратко

Привет, Вы узнаете о том , что такое 6. Сопряженный оператор. Условия существования сопряженного оператора. Замкнутость сопряженного оператора. Сопряженный оператор к ограниченному оператору и его норма., Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 6. Сопряженный оператор. Условия существования сопряженного оператора. Замкнутость сопряженного оператора. Сопряженный оператор к ограниченному оператору и его норма. , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Пусть X – банахово пространство и А – ограниченный линейный оператор, определенные на Х, с областью значений в банаховом пространстве Y. Пусть х ÎХ и f ÎY*. Тогда определено значение f(Ax), при этом выполняются неравенства | f(Ax)| £ ||f ||×||Ax|| £ ||f ||×||A||×||x||. Эти неравенства показывают, что линейный функционал j(х), определенный равенством j(х) = f(Ax), является ограниченным функционалом. Таким образом, каждому линейному ограниченному функционалу f ÎY с помощью оператора А ставится в соответствие линейный непрерывный функционал j ÎХ*. Меняя элемент f мы будем получать, вообще говоря, разные элементы j; тем самым мы получаем оператор

j = A*f,

определенный на Y*, с областью значений в пространстве X*. Этот оператор A* связан с оператором А равенством (A*f)(x) = f(Ax). Если применить введенное в п. 2 обозначение для линейного функционала f(x) = (x, f), то связь операторов будет выглядеть симметрично:

(Ax, f)=(x, A*f). (1)

Оператор A* однозначно определяется формулой (1) и называется оператором, сопряженным с оператором А.

Действительно, если для всех x и y имеют место равенства

(Ax, y) = (x, A*y) = ( x, A1*y),

то отсюда по следствию 4 из теоремы Хана-Банаха следует, что A1*y= A*y для всех y, а это означает, что A*=A1*.

Теорема 11. Сопряженный оператор A* – линейный и .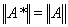

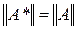Доказательство. Докажем аддитивность оператора A*. Об этом говорит сайт https://intellect.icu . Действительно, если y, z ÎY*, то из рассуждений выше вытекает существование единственного элемент (y + z)* ÎX, что (Ax, y + z)=(x, (y + z)*) при всех x ÎX.

С другой стороны, с помощью формулы (1) имеем

(Ax, y + z) = (Ax, y) + (Ax, z) = (x, A*y) + (x, A*z) = (x, A*y + A*z) = (x, (y+z)*),

т.е. (y+z)* = A*x + A*y, откуда A*(y+z)=A*y+A*z. Это доказывает аддитивность оператора А*. Однородность также легко проверяется.

Для вычисления нормы оператора А* проведем оценки

.

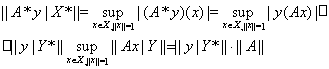
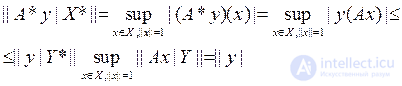Отсюда следует, что оператор A* – ограниченный и .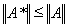

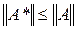У оператора A*, в свою очередь, есть сопряженный – A**, определяемый равенством, аналогичным (1)

(A*y, x) = (y, A**x) (2).

Но, так как из (2) A**x определяется однозначно для каждого xÎХ, то из сопоставления равенств (1) и (2) следует, что

(Ax, y) = (A**x, y) "хÎХ, "yÎY.

В силу следствия 4 из теоремы Хана-Банаха последнее означает, что A**x=Ax для всех xÎX, т.е. A**= A на пространстве Х. Применяя доказанное неравенство для нормы сопряженного оператора к A* и A**, имеем 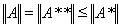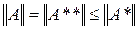, что и дает требуемое равенство: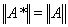 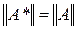. Теорема доказана.

Теорема. 12. Если А и В линейные ограниченные операторы из банахова пространства Х в банахово пространство Y, то

1. (А+В)*=А*+В*

2. (λА)*= λА*

3. В предположении Х = Y, справедливо равенство (АВ)*=В*А*.

Доказательство. Вышеуказанные свойства вытекают из следующих соотношений:

1. ((A+B)x, y) = (Ax, y) + (Bx, y) =(x, A*y) + (x, B*y) = (x, (A* + B*)y);

2. ((λA)x ,y) = λ(Ax ,y) = λ(x, A*y) = (x, ( λA*y));

3. ((AB)x, y) = (A(Bx), y) = (Bx, A*y) = (x, B*(A*y)) = (x, (B*A*)y).

Теорема доказана.

Пример 8. В пространстве L2[a,b] рассмотрим интегральный оператор Фредгольма

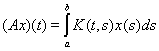
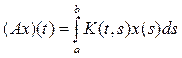
с ядром, имеющим интегрируемый квадрат. Имеем, используя теорему Фубини,

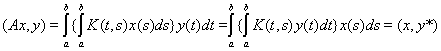
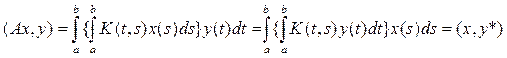, где

.

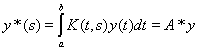
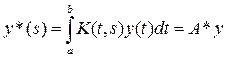Таким образом, переход к сопряженному оператору заключается в том, что интегрирование ведется по первой переменной. Тогда как в исходном операторе оно ведется по второй.

Исследование, описанное в статье про 6. Сопряженный оператор. Условия существования сопряженного оператора. Замкнутость сопряженного оператора. Сопряженный оператор к ограниченному оператору и его норма., подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 6. Сопряженный оператор. Условия существования сопряженного оператора. Замкнутость сопряженного оператора. Сопряженный оператор к ограниченному оператору и его норма. и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ