7. Отображение компактных множеств. Теорема Вейерштраса об ограниченности и достижении точных граней непрерывной функцией кратко

Привет, Вы узнаете о том , что такое 7. Отображение компактных множеств. Теорема Вейерштраса об ограниченности и достижении точных граней непрерывной функцией, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 7. Отображение компактных множеств. Теорема Вейерштраса об ограниченности и достижении точных граней непрерывной функцией , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Теорема 9. Пусть Х, У – топологические пространства, Х компактно, а f: Х ® У – непрерывное отображение. Тогда образ f(Х) – компактное пространство в У.

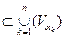Доказательство. Пусть {Va} - произвольное открытое покрытие f (Х). В силу определения непрерывного отображения, множества f -1(Va) также являются открытыми и, очевидно, образуют открытое покрытие для Х. В силу компактности Х существует конечный набор из этого покрытия такой, что . Но в этом случае и f (Х) , что доказывает компактность f (Х).

Теорема 10. Пусть Х, У – топологические пространства, Х компактно, У – отделимое, а f: Х ® У – непрерывное отображение. Тогда f замкнутое отображение.

Доказательство. Всякое замкнутое множество компактного пространства само является компактным множеством (теорема 1.13). Итак, пусть В – замкнутое множество в пространстве Х (следовательно компактное). Об этом говорит сайт https://intellect.icu . По предыдущей теореме f (В) – компактное множество. В силу отделимости У это множество обязано быть замкнутым (теорема 1.15).

Теорема 11. Пусть Х, У – топологические пространства, Х компактно, У – отделимое, а f: Х ® У – непрерывное биективное отображение. Тогда f - гомеоморфизм.

Доказательство практически очевидное.

Теорема 12 (Вейерштрасса). Всякая непрерывная функция f : Х ® R на компактном пространстве Х ограничена и достигает на Х своей верхней (нижней) грани.

Доказательство. В силу компактности Х и непрерывности f образ f (X) является компактным множеством в R. Но любое компактное множество в R ограничено и замкнуто. Ограниченность f (X) означает ограниченность функции. Замкнутость числового множества f (X) влечет принадлежность ему его точных граней. Это означает, что точная грань (например, супремум) достигается на каком-то элементе х0 ÎХ, т.е. f (x0) = sup f (X).

Теорема 13 (Кантора). Всякая непрерывная функция f(x), определенная на компактном множестве Q, метрического пространства (Х, r), равномерно непрерывна на нем: иными словами, для любого ε > 0 можно найти такое δ>0, что из ρ(x, y)< δ следует |f(x) - f(y)| < ε

Доказательство. Допуская противное, мы для некоторого ε0 сможем указать такие последовательности xn и yn, что

ρ (xn, yn)< , |f(xn) - f(yn)| 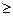ε0 (12)

Последовательность {xn} в силу предположения содержит подпоследовательность {xni}, сходящуюся к некоторой точке х0. Тогда и подпоследовательность {yni} сходится к точке х0. Начиная с некоторого номера, точки xni и yni попадают в такую окрестность точки х0 , в которой выполняется неравенство |f(x ) - f(x0)|< 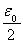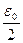. Но тогда

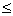
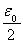
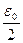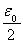
|f(xni ) - f(yni)| |f(xni) - f(х0)| + |f(x0) - f(yni)| < + 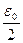= ε0

что противоречит условию (12). Теорема доказана.

Исследование, описанное в статье про 7. Отображение компактных множеств. Теорема Вейерштраса об ограниченности и достижении точных граней непрерывной функцией, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 7. Отображение компактных множеств. Теорема Вейерштраса об ограниченности и достижении точных граней непрерывной функцией и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ