3. Функция множеств кратко

Привет, Вы узнаете о том , что такое 3. Функция множеств, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 3. Функция множеств , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Определение 14. Вещественнозначная функция, областью определения которой является некоторая система множеств Â, называется функцией множества.

Определение 15. Функция f называется счетно-аддитивной, если для любой не более чем счетной совокупности дизъюнктных множеств An Î Â, объединение которых А = 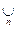An тоже принадлежит Â, имеет место равенство

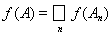
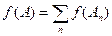
Определение 16. Если равенство ограничено случаем, когда А есть объединение конеч­ного числа дизъюнктных множеств Аn (А, Аn Î Â), то функция f называется конечно-аддитивной или просто аддитивной.

Так как функции могут принимать бесконечные значения необходимо договориться об арифметических операциях над символами бесконечность. В основном эти правила аналогичные тем, которые применялись в математическом анализе. Например: ¥ ± а = ¥; ¥ + ¥ = ¥ и т.п. Но есть определенные отличия. Так мы полагаем, что 0´¥ = 0 и ¥ - ¥ = -¥ - (-¥) = 0. В математическом анализе последние два действия полагались неопределенностью.

Лемма 2. Если функция множеств f является аддитивной, принимает конечные значения на множествах А, В, В\А ÎÂ и А Ì В, то f(B\A) = f(B) – f(A).

Утверждение легко вытекает из дизъюнктного представления В = А + В\А.

Следствие. Об этом говорит сайт https://intellect.icu . Если функция множеств f является аддитивной, неотрицательной, принимает конечные значения на множествах А, В, В\А ÎÂ и А Ì В, то f(B) ³ f(A).

Теорема 4. Для того, чтобы аддитивная функция f, принимающая конечные значения и задан­ная на кольце K, была счетно-аддитивной, необходимо и достаточно, чтобы для любой убывающей после­довательности множеств Аi Î K (i = 1,2,...), т.е. таких что А1 É А2 É А3 É …, с пустым пересечением выполнялось f(Ai) ® 0 при i ®¥.

Необходимость. Пусть Аi убывающая последовательность множеств, т.е., при этом 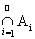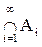= Æ. Построим систему непересекающихся множеств Bi = Ai\Ai+1. Тогда нетрудно видеть, что А1 =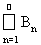 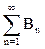. В силу счетной аддитивности функции множеств f(A1) =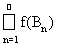 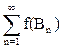. Последнее равенство означает, что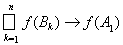 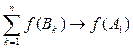при n ® ¥. Но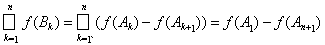 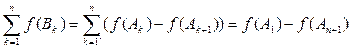. Последнее равенство в сочетание с поведением частичных сумм доказывает утверждение.

Достаточность. Пусть дизъюнктные множества An Î K, объединение которых А = 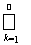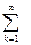Ak тоже принадлежит K. Построим последовательность убывающих множеств Вn = A\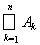 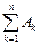. В силу леммы, аддитивности функции множества и условий теоремы f(Bn) = f(A) – f(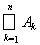 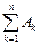) = f(A) -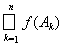 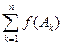® 0. Последнее доказывает счетную аддитивность функции множеств.

Следующая теорема доказывается аналогично.

Теорема 5. Пусть f - счетно-аддитивная функция, заданная на кольце K. Если А ÎK и А = 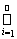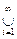Аi, где Ai ÎK и образуют возрастающую последовательность, т.е. А1 Ì А2 Ì…, то

f(A) = 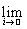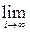f(Ai).

То же равенство справедливо, если А = 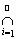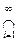Аi (А, Аi Î K), Аi образуют убывающую последовательность и f(Ai) конечные числа, начиная с некоторого i.

Исследование, описанное в статье про 3. Функция множеств, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 3. Функция множеств и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ