Лекция
Привет, Вы узнаете о том , что такое 2. Теорема о пополнении метрического пространства, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 2. Теорема о пополнении метрического пространства , настоятельно рекомендую прочитать все из категории Функциональный анализ.
Если метрическое пространство не является полным, то существует его пополнение. Для введения этого пополнения приведем еще ряд определений. Пусть существует два метрических пространства (X, d), (Y, p) и f – биекция X на Y.
Определение 5. Биекция f называется изометрическим изоморфизмом, если p(f(x), f(y)) = d(x, y).
Два метрических пространства изометрически изоморфные друг другу отождествляются.
Например, пространства C[0, 1] и C[0, 2] непрерывных функций на отрезках [0, 1] и [0, 2] соответственно являются изометричными. Изометрический изоморфизм между их элементами можно установить по формуле
C[0, 1] 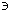
 x(t)
x(t) 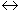
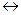 y(t)=x(
y(t)=x( 
 )
) 
 C[0, 2].
C[0, 2].
Определение 6. Пусть (X, d) - метрическое пространство и Y Ì X. Множество Y называется всюду плотным в Х, если для "e>0, "xÎX $ yÎY: d(x, y)<e.
Теорема 1. Пусть дано неполное метрическое пространство (X, d), тогда существует такое полное метрическое пространство (Y, p) и его всюду плотное подпространство Y0, что (X, d) изометрически изоморфно (Y0, p).
Доказательство. Пусть {xn} и {yn} - фундаментальные последовательности в Х. Будем считать, что {xn} ~ {yn} Û 
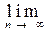 d(xn, yn) = 0 (свойства отношения эквивалентности легко проверяются). Пусть [xn] - класс эквивалентности, а Y- множество всех классов эквивалентности фундаментальных последовательностей. Положим r([xn], [yn]) =
d(xn, yn) = 0 (свойства отношения эквивалентности легко проверяются). Пусть [xn] - класс эквивалентности, а Y- множество всех классов эквивалентности фундаментальных последовательностей. Положим r([xn], [yn]) = 
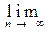 d(xn, yn).
d(xn, yn).
Для доказательства корректности этого определения необходимо показать: 1) существование предела, 2) независимость его от выбора элементов из класса эквивалентности, 3) выполнение аксиом метрики.
1) Из неравенства четырехугольника следует, что |d(xn, yn) - d(xm, ym)| £ d(xn, xm) + d(yn, ym). Так как последовательность {xn} и {yn} фундаментальны, то для " e > 0 $N: "n, m ³ N d(xn, xm) < e/2 и d(yn, ym) < e/2. Обозначим через an = d(xn, yn). Из полученных выше неравенств вытекает, что при " e > 0 $N: "n, m ³ N имеем |an - am| < e и следовательно последовательность an фундаментальная, т. е. существует предел этой числовой последовательности. Таким образом, нужный предел существует и метрика r ([xn], [yn]) = 
 d(xn, yn) определена.
d(xn, yn) определена.
2) Докажем, что это определение не зависит от выбора представителя класса эквивалентности. Об этом говорит сайт https://intellect.icu . Пусть {xn}, {x*n}Î[xn], {yn}, {y*n}Î[yn]. Тогда d(x*n, y*n) £ d(x*n, xn) + d(xn, yn) + d(yn, y*n). В силу определения классов эквивалентности имеем 
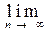 d(x*n, xn) = 0 и
d(x*n, xn) = 0 и 
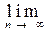 d(y*n, yn) = 0. Следовательно,
d(y*n, yn) = 0. Следовательно, 
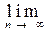 d(x*n, y*n) £
d(x*n, y*n) £ 
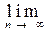 d(xn, yn). Последнее неравенство было установлено для произвольных представителей класса эквивалентности. Тогда поменяв местами xn и x*n, yn и y*n, получим противоположное неравенство. Итак,
d(xn, yn). Последнее неравенство было установлено для произвольных представителей класса эквивалентности. Тогда поменяв местами xn и x*n, yn и y*n, получим противоположное неравенство. Итак, 
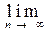 d(x*n, y*n) =
d(x*n, y*n) = 
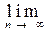 d(xn, yn).
d(xn, yn).
3) Аксиомы метрики легко доказываются при помощи предельного перехода.
Таким образом, мы установили, что (Y, p) - метрическое пространство. Докажем, что оно полно. Пусть {[xn](m)} - фундаментальная последовательность в Y. Надо доказать, что [xn](m) ® [xn](0) Î Y. Пусть {xn(m)}Î[xn](m) . Так как для любого m последовательности {xn(m)} фундаментальны, то для "р $ kp: "n ³ kр
d(xn(р) , 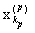
 ) < 1/р. (1)
) < 1/р. (1)
Построим последовательность { 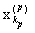
 }. Имеем
}. Имеем
d( 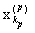
 ,
, 
 ) £ d(
) £ d( 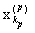
 , xm(p)) + d(xm(p), xm(n)) + d(xm(n),
, xm(p)) + d(xm(p), xm(n)) + d(xm(n), 
 ).
).
В силу неравенства (1) за счет выбора m, kp, kn можно первое и третье слагаемое в правой части этого неравенства сделать меньше любого наперед заданного числа. Так как {[xn](m)} – фундаментальная последовательность, то справедливо 
 r([xk](m), [xk](n)) = 0. Из определения метрики r на Y r ([xk](m), [xk](n)) =
r([xk](m), [xk](n)) = 0. Из определения метрики r на Y r ([xk](m), [xk](n)) = 
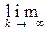 d(xk(m), хk(n)) вытекает, что и второе слагаемое можно сделать меньше любого наперед заданного числа. Таким образом, последовательность {
d(xk(m), хk(n)) вытекает, что и второе слагаемое можно сделать меньше любого наперед заданного числа. Таким образом, последовательность { 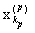
 } фундаментальна в Х. Обозначим класс ее эквивалентности через [xn](0). Покажем, что [xk](m) ® [xn](0). Очевидно, имеем r ([xn](0), [xk](m)) =
} фундаментальна в Х. Обозначим класс ее эквивалентности через [xn](0). Покажем, что [xk](m) ® [xn](0). Очевидно, имеем r ([xn](0), [xk](m)) = 
 d(
d( 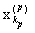
 , xp(m)) £
, xp(m)) £ 
 d(
d( 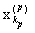
 ,
, 
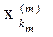 ) +
) + 
 d(
d( 
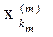 , xp(m)) <
, xp(m)) < 
 d(
d( 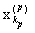
 ,
, 
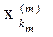 ) + 1/m. Последний предел, стоящий в неравенстве, в силу фундаментальности последовательности
) + 1/m. Последний предел, стоящий в неравенстве, в силу фундаментальности последовательности 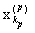
 может быть сделан за счет выбора m коль угодно маленьким. Это означает, что [xk](m) ® [xn](0) в Y.
может быть сделан за счет выбора m коль угодно маленьким. Это означает, что [xk](m) ® [xn](0) в Y.
Рассмотрим [xn = x] - стационарную фундаментальную последовательность, xÎX, порождающую класс эквивалентности [х]. Обозначим через Y0 - множество всех классов эквивалентности стационарных последовательностей в Х. Докажем, что Y0 изометрически изоморфно X.
Пусть хÎX. Тогда этому элементу соответствует стационарная фундаментальная последовательность [х] ÎY0. Очевидно, что такое соответствие является сюрьекцией. Докажем, что это и иньекция. Пусть x ¹ y. Тогда
r ([x], [y]) = lim d(x, y) ¹ 0 Þ r ([x], [y]) ¹ 0 Þ [x] ¹ [y].
Таким образом, данное отображение биекция, при этом r ([х], [у]) = lim d(x, y) = d(x, y) (изометрия).
Пусть [хn]ÎY. Тогда {хn} - фундаментальная последовательность в Х, т.е. для "e>0 $ s: d(xp, xm) < e при всех p, m > s. Построим стационарную последовательность {x = xs}. Тогда [x]ÎY0 и p([x], [xk]) = 
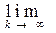 d(xs, xk). В силу выбора s при достаточно больших k выполняется неравенство d(xs, xk) < e. Этим показана плотность Y0 в пространстве Y и доказательство теоремы завершено.
d(xs, xk). В силу выбора s при достаточно больших k выполняется неравенство d(xs, xk) < e. Этим показана плотность Y0 в пространстве Y и доказательство теоремы завершено.
Исследование, описанное в статье про 2. Теорема о пополнении метрического пространства, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 2. Теорема о пополнении метрического пространства и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ
Из статьи мы узнали кратко, но содержательно про
Комментарии
Оставить комментарий
Функциональный анализ
Термины: Функциональный анализ