Привет, Вы узнаете о том , что такое 7. Мера Лебега на Rn, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 7. Мера Лебега на Rn , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Пусть m мера, простроенная по теореме 7 на полукольце ячеек. Эта мера порождает внешнюю меру (теорема 8). Мера, порожденная этой внешней мерой на множествах из Rn называется мерой Лебега на Rn.

Следующая теорема является аналогом ранее доказанной теоремы о структуре открытых множеств на числовой прямой.

Теорема 13. Всякое открытое множество G Ì Rn представимо в виде не более чем счет­ного объединения дизъюнктных n-мерных открытых параллелепипедов с конечными ребрами.

Теорема 14. Каждое открытое и каждое замкнутое множество из Rn измеримо.

Доказательство. Легко вытекает из того, что все ячейки в Rn измеримы по теореме 9, далее система измеримых множеств s-алгебра (теорема 9) и любой открытый параллелепипед можно представить в виде счетного объединения возрастающей последовательности ячеек. Воспользовавшись теперь теоремой 13 и снова замкнутостью системы измеримых множеств относительно счетного объединения, получим измеримость любого открытого множества. Измеримость замкнутых множеств получается опять же в силу замкнутости системы измеримых множеств относительно операции дополнения.

Теорема 15. Любой параллелепипед D измерим, при этом m(D) = VD.

Доказательство. Доказательство легко вытекает из вложений D0ÇЕ Ì DÇЕ Ì D*ÇЕ и вытекающего отсюда неравенства внешних мер m*(D0ÇЕ) £ m*(DÇЕ) £ m*(D*ÇЕ), а также равенства m*(D*\D0) = 0.

Теорема 16. Всякое конечное или счетное множество А точек из Rn измеримо и его мера равна 0.

Доказательство. Пронумеруем точки множества А в виде последовательности zn. Возьмем произвольное e > 0. Поместим каждую точку в n-мерный куб (открытый или замкнутый), объем которого не превосходит e/2n. Тогда m*(А) £ e. В силу теоремы 11 это означает, что множество А измеримо и имеет меру 0.

Определение 28. Борелевскими множествами называют множества, принадлежащие наименьшей s-алгебре множеств, содержащей все открытые и замкнутые множества в Rn.

Так как по теореме 14 все открытые и замкнутые множества измеримы, а все измеримые множества образуют s-алгебру, то очевидна следующая теорема.

Теорема 17. Все борелевские множества из Rn измеримы.

Теорема 18. Внешняя мера любого множества Е Ì Rn равна нижней грани мер всевоз­можных открытых множеств, содержащих Е

m*(Е) = 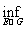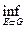μ(G)

Доказательство. Утверждение практически очевидно, так как, покрывая множество ячейками, мы легко можем покрыть это множество открытыми параллелепипедами, объем которых в совокупности отличается от объема покрытия ячейками на сколь угодно малое положительное число.

Теорема 19. Мера любого ограниченного измеримого множества Е Ì Rn равна верхней грани мер всевоз­можных замкнутых множеств, содержащихся в Е

m(Е) = μ(F)

Доказательство. Поместим множество Е в некий замкнутый ограниченный параллелепипед Р. При этом предполагаем, что внутренность параллелепипеда Р также содержит множество Е. В силу ограниченности множества Е это можно сделать. В силу свойств меры множество Р – Е измеримо. Из теоремы 18 и свойств меры вытекает (в силу условий на Р наименьшую грань можно брать только по открытым множествам содержащимся в Р):

m(Е) = m(Р – (Р – Е)) = m(Р) - m(Р – Е) = m(Р) - 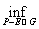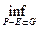μ(G) = 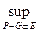m(Р – G).

В силу открытости множества G множество F = P – G является замкнутым. Отсюда вытекает утверждение теоремы.

Задачи

1. Доказать, что система всех конечных подмножеств заданного множества является кольцом.

2. Найти в задаче 1. условие на множество 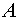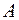, необходимое и достаточное для того, чтобы кольцо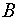 являлось алгеброй.

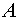
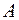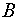
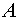
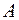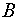
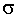
3. Пусть – бесконечное множество, а – система всех не более чем счетных подмножеств . Об этом говорит сайт https://intellect.icu . Доказать, что является -кольцом.

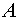
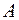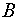
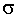
4. Найти в задаче 3. условие на , необходимое и достаточное для того, чтобы являлось -алгеброй.

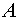
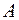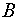
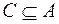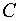
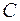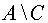
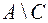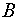
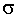
5. Пусть – множество, – система всех таких множеств , что либо , либо не более чем счетно. Доказать, что является -алгеброй.

6. Пусть 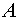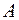– множество,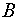 – система всех таких множеств 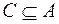, что либо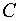 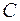, либо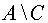 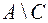конечно. Доказать что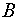 является алгеброй.

7. Доказать, что система всех интервалов, отрезков и полуинтервалов из отрезка 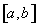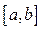образует полукольцо.

8. Доказать, что система всех интервалов (включая пустой) и система всех отрезков (с добавлением пустого множества) в R не является полукольцом.

9. Доказать, что система всех открытых множеств в R не является полукольцом.

10. Пусть 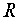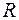– полукольцо (кольцо),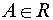 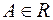. Доказать, что система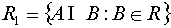 – полукольцо (алгебра) (эту систему мы будем обозначать через ).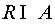

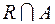11. Построить систему множеств, которая замкнута относительно операци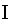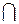й и 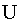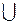, но не является даже полукольцом.

12. Пусть 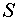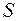– полукольцо. Доказать, что система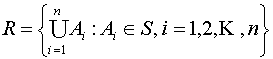 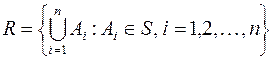является кольцом.

13. Пусть 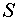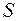– полукольцо. Доказать, что система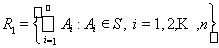 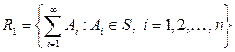совпадает с кольцом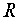 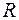, определенным в задаче 12.

14. Доказать, что пересечение произвольной непустой системы колец является кольцом (возможно, кольцом ).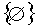

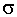
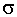
15. Доказать, что пересечение произвольной непустой системы -колец является -кольцом.

16. Доказать, что пересечение произвольной системы алгебр с одной и той же единицей является алгеброй.

17. Привести пример двух 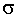-алгебр, пересечение которых не является алгеброй.

18. Доказать, что не существует кольца, содержащего ровно 3 различных множества (включая пустое).

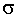
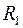19. Построить пример -алгебр и 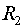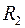таких, что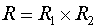 не является кольцом.

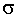
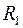20. Доказать, что произведение -алгебр и 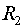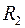с единицам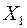и и 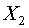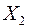является кольцом тогда и только тогда, когда хотя бы одна из этих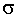 -алгебр содержит не более двух множеств.

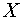
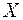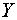
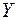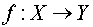
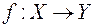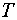
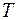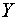
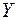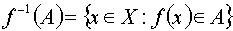
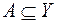21. Пусть даны множества и , функция , а – система множеств в . Положим для и 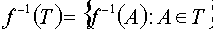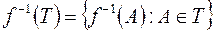. Доказать, что если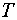 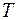– полукольцо, то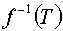 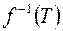– полукольцо.

22. В условиях задачи 21 доказать, что если 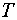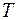– кольцо, то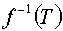 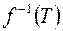– тоже кольцо.

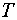
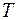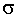
23. В условиях задачи 21 доказать, что если – -алгебра, то 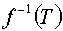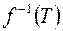– тоже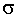 -алгебра.

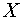
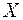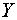
24. Построить множества , , 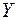функцию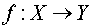 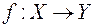и кольцо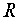 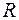подмножеств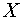 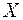такие, что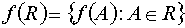 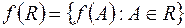не является полукольцом.

25. Пусть задано полукольцо P1 промежутков [a, b) (см. теорема 3) и неубывающая ограниченная функция g(x) на числовой прямой. Определим функцию множеств m([a, b)) = g(b) – g(a). Доказать, что m является счетно-аддитивной мерой на P1 тогда и только тогда, когда функция g(x) непрерывна слева во всех точках. (Замечание. Мера, которая получается из этой меры при продолжении называется мерой Лебега-Стильтьеса).

Исследование, описанное в статье про 7. Мера Лебега на Rn, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 7. Мера Лебега на Rn и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ