2. Основные свойства интеграла от ограниченной функции кратко

Привет, Вы узнаете о том , что такое 2. Основные свойства интеграла от ограниченной функции, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 2. Основные свойства интеграла от ограниченной функции , настоятельно рекомендую прочитать все из категории Функциональный анализ.

В этом пункте мы установим ряд свойств интеграла от огра­ниченной измеримой функции.

Теорема 3 (о среднем). Если измеримая функция f(x) на измеримом мно­жестве Е удовлетворяет неравенствам a £ f(x) £ b, то a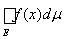×m (E) £ £ b×m (E).

Доказательство. Если мы положим A = a, B = b в определении интеграла, то окажется, что A £ f(x) £ B, и суммы Лебега можно будет составлять, дробя отрезок [А, В]. Но если A £ yk £ B, то, очевидно,

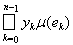
A £ £ B

или, что то же самое, a×m (E) £ s £ b×m(E),откуда и в пределе

a×m (E) £ £ b×m (E).

Теорема доказана.

Из этой теоремы вытекает несколько простых следствий.

Следствие 1. Если функция f(x) постоянна на измеримом множестве Е и f(x) = с, то

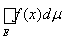
= c× m(E).

Следствие 2. Если функция f(x) не отрицательна (не положи­тельна), то таков же и ее интеграл.

Следствие 3. Если m (Е) = 0, то для любой ограниченной функ­ции f(x), заданной на множестве Е, будет 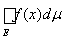= 0.

Теорема 4 (полная или счетная аддитивность интеграла по области интегрирования). Пусть на измеримом множестве Е задана изме­римая ограниченная функция f(x). Если множество Е есть сумма конечного числа или счетного множества попарно не пересекаю­щихся измеримых множеств E = 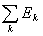(EkÇEi = Æ, k ¹ i ), то

=

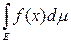Доказательство. Рассмотрим сначала простейший случай, когда число слагаемых равно двум Е = E1 + E2 (E1Ç E2 = Æ. Если на множестве Е A £ f(x) £ B и мы, раздробив отрезок [А, В] точками у0, y1,¼ , уn, составим множества ek = E(yk £ f < yk+1), ek¢= E1(yk £ f < yk+1), ek¢¢= E2(yk £ f < yk+1), то, очевидно, будем иметь ek = ek¢ + ek¢¢ (ek¢Çek¢¢ = Æ), откуда

= +

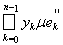
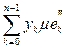
и в пределе, при l ® 0,

= +

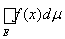
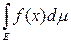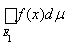
Итак, теорема доказана для случая двух слагаемых множеств. Об этом говорит сайт https://intellect.icu . Пользуясь методом математической индукции, мы легко распространим теорему на случай любого конечного числа слагаемых множеств. Остается рассмотреть случай, когда E = 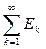. В этом случае

= m (E),

так что при n ® ¥ в силу свойства непрерывности меры будет ® 0. Заметив это, положим 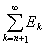= Rn, причем m(Rn) ® 0 при n ® ¥. Так как для конечного числа слагаемых множеств теорема уже дока­зана, то

= + .

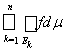
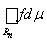
В силу теоремы о среднем A×m (Rn) £ 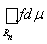£ B×m (Rn), а в силу стремления меры множества Rn к нулю с возраста­нием n, ясно, что 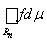® 0. Но это и означает, что

=

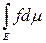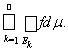
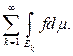
Из этой теоремы вытекает ряд следствий.

Следствие 1. Если измеримые ограниченные функции f(x) и g(x), заданные на множестве Е, эквивалентны между собой, то = .

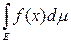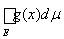
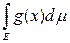Действительно, если H = Е(f ¹ g), G = E(f = g), то m(H) = 0 и 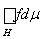= = 0.

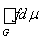
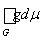
На множестве же G обе функции тождественны и = . Остается сложить это равенство с предыдущим.

В частности, интеграл от функции, эквивалентной нулю, равен нулю.

Достаточно очевидно, что последнее утверждение необратимо. Например, если f(x) задана на отрезке [–1, +1], так:

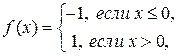
то

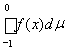
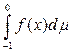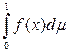= + = -1 + 1 = 0,

хотя функция f(x) и не эквивалентна нулю.

Однако справедливо

Следствие 2. Если интеграл от неотрицательной из­меримой ограниченной функции f(x) равен нулю 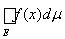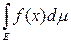(f(x) ³ 0), то эта функция эквивалентна нулю.

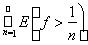
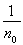
В самом деле, легко видеть, что E(f > 0) = . Если бы f(x) не была эквивалентна нулю, то необходимо на­шлось бы такое n0, что mE = s > 0. Полагая A = E , B = Е - A, мы имели бы, что ³ s, 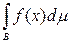³ 0, и, складывая эти неравенства, мы получили бы 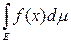³ 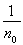s, что противоречит условию.

Теорема 5 (свойство аддитивности интеграла). Если на измеримом множестве E заданы две измеримые ограниченные функции f(x) и g(x), то

= + .

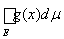
Доказательство. Следующие неравенства достаточно очевидны:

d(a, f ) + d(a, g ) £ d(a, f + g ) £ D(a, f + g ) £ D(a, f ) + D(a, g ).

В силу следствия теоремы 1 крайние члены этих неравенств можно сделать сколько угодно близкими. Последнее предельным переходом приводит к необходимым равенствам.

Теорема 6 (свойство однородности интеграла). Если на измеримом множестве Е задана изме­римая ограниченная функция f(x) и с есть конечная постоянная, то

= c .

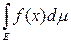Доказательство. Утверждение очевидно при с = 0.

Пусть c > 0 и А £ f(x) £ B. Разбиваем отрезок [A, B] и вводим множества ek. В силу теоремы о полной аддитивности по области интегрирования получаем

.

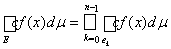
Но на множестве ek функция f(x) удовлетворяет неравенствам сyk £ f(x) < cyk + 1, так что в силу теоремы о среднем

.

Сложив все такие неравенства, получим

,

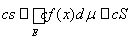
где s и S – интегральные суммы Лебега функции f(x). Нужное равенство получается предельным переходом в этих неравенствах и из теоремы 2.

Пусть, наконец, c < 0. Тогда

,

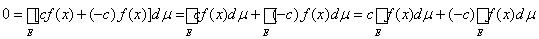
откуда следует теорема.

Следствие. Если f(x) и F(х) измеримы и ограничены на мно­жестве Е, то

= – .

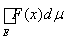
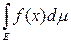Теорема 7. Пусть f(x) и F(х) измеримы и ограничены на измеримом множестве Е. Если f(x) £ F(x), то

£ .

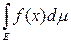Теорема 8. Если функция f(x) измерима и ограничена на измеримом множестве E, то

£

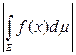Теоремы доказываются стандартно, как соответствующие неравенства для интеграла Римана.

Исследование, описанное в статье про 2. Основные свойства интеграла от ограниченной функции, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 2. Основные свойства интеграла от ограниченной функции и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ

Из статьи мы узнали кратко, но содержательно про