6. Измеримые множества кратко

Привет, Вы узнаете о том , что такое 6. Измеримые множества, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 6. Измеримые множества , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Пусть Х – фиксированное множество, на котором задана внешняя мера m*.

Определение 23. Пусть А, Е Ì Х. Множество А хорошо разбивает множество Е, если

m*(Е) = m*(ЕÇА) + m*(ЕÇАС) (2)

Определение 24. Назовем множество А Ì X m*-измеримым, если оно хорошо разбивает любое множество Е Ì X.

Сужение внешней меры m* на совокупность всех m*-измеримых множеств обозначим через m.

Заметим, что в силу полуаддитивности внешней меры для любого Е Ì Х выполняется неравенство:

m*(Е) £ m*(ЕÇА) + m*(ЕÇАС).

Поэтому для доказательства измеримости данного множества А достаточно проверить справедливость лишь противоположного не­равенства. Отметим также, что если m*(Е) = ¥ это неравенство выполняется автоматически и достаточно его проверять на множествах Е, для которых m*(Е) < ¥.

Теорема 9а. Система S всех m* -измеримых множеств в X – алгебра.

Доказательство. Достаточно очевидно, что ХÎS: m*(E) = m*(EÇX) + m*(EÇÆ). Поэтому необходимо проверить лишь условия кольца. С другой стороны из симметричности определения измеримого множества вытекает, что множество А и его дополнение АС являются измеримыми одновременно.

Пусть теперь А, В ÎS. Для любого множества Е Ì Х справедлива следующая цепочка равенств:

m*(ЕÇ(АÈВ)) + m*(ЕÇ(АÈВ)С) = m*((ЕÇ(АÈВ))ÇА) +m*((ЕÇ(АÈВ))ÇАС) + m*(ЕÇАСÇВС) =

= m*(ЕÇА) +m*(ЕÇВÇАС) + m*(ЕÇАСÇВС) = m*(ЕÇА) +m*(ЕÇАС) = m*(Е).

(первое равенство получено в силу измеримости множества А – добавили к фиксированному множеству (ЕÇ(АÈВ)); второе равенство – использование свойств операций над множествами; третье равенство – объединение второго и третьего слагаемого и использование измеримости В; последнее – измеримость множества А).

Таким образом, показана замкнутость S относительно операции конечного объединения. Отсюда, отмеченного выше факта о замкнутости S относительно операции дополнения и теорем двойственности де Моргана вытекает замкнутость S относительно пересечения множеств.

Так как А\В = АÇВС, то S является алгеброй.

Теорема 9б. Функция m - аддитивна на S.

Доказательство. Пусть В, С Î S и А = В + С. В силу измеримости В справедливо равенство:

m*(А) = m*(АÇВ) + m*(АÇВС) = m*(В) + m*(С).

Последнее равенство вытекает из простых множественных равенств: АÇВ = В, АÇВС = С.

Теорема 9в. Система S всех m* -измеримых множеств в X – s-алгебра.

Доказательство. Пусть А = 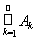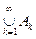, где Аk Î S. Нам необходимо показать, что АÎS, т.е. выполняется равенство m*Е = m*(ЕÇА) + m*(ЕÇАС) для любого Е Ì Х. Построим систему множеств из S следующим образом: С1 = А1, С2 = А2\А1, …, Cn = An\ , … Из построения ясно, что СnÎS и А = 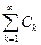. Введем множество Вn =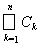 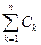ÎS. Справедливы равенства:

m*(EÇBn) = m*(EÇBnÇC1) + m*(EÇ BnÇC1C) = m*(EÇC1) + m*(EÇ ) =

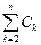= m*(EÇC1) + m*(EÇ 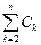ÇC2) + m*(EÇ 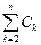ÇC2C) =

= m*(EÇC1) + m*(EÇC2) + m*(EÇ ) = … = .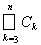

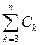Далее

m*(Е) = m*(EÇBn) + m*(EÇBnС) = + m*(EÇBnС) ³ + m*(EÇАС).

Последнее неравенство получено в силу монотонности внешней меры и вложения АС Ì BnС. Об этом говорит сайт https://intellect.icu . Последнее неравенство верно для любого n. Переходя в нем к пределу по n, получим неравенство:

m*(Е) ³ + m*(EÇАС).

Воспользуемся теперь счетной полуаддивностью внешней меры:

³ 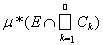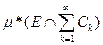= m*(ЕÇА).

Тогда m*(Е) ³ m*(ЕÇА) + m*(EÇАС), что с учетом замечания, сделанного после определения измеримого множества, доказывает измеримость А.

Теорема 9г. Функция m – мера на S.

Доказательство. Пусть А, Аk ÎS и А = 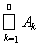. В силу доказанной конечной аддитивности функции m, справедливо равенство 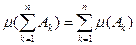. Так как Ì А, то

.

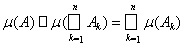
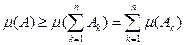Предельным переходом по n отсюда получаем неравенство 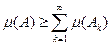. Если теперь вспомнить, что внешняя мера обладает свойством счетной полуаддитивности, т.е.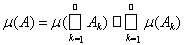 , то получаем необходимое равенство.

Объединяя теоремы 9а, 9б, 9в и 9г, получаем.

Теорема 9. Система S всех m* -измеримых множеств в X – s-алгебра, а m – мера на S.

Определение 25. Будем говорить, что мера m, построенная в этой теореме, порождена внешней мерой m*.

Теорема 10 Пусть m – мера в X, заданная на полукольце P, m* – внешняя мера, поро­жденная мерой m, m – мера, порожденная внешней мерой m*, тогда m – продолжение m на s-алгебру S m*-измеримых множеств, т.е. P Ì S и m(А) = m(А) для А ÎP.

Доказательство. Равенство m(А) = m(А) для всех А ÎP по существу установлено в теореме 8. Требуется проверить, что любое А ÎP удовлетворяет равенству (2).

Пусть Е Ì Х, m*(Е) < ¥ и по определению внешней меры, порожденной m для произвольного e > 0 найдено покрытие АkÎP такое, что Е Ì Ak и m*(Е) > 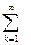m(Ak) – e. Так как ЕÇА Ì 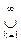(AkÇА) и ЕÇАС Ì 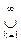(AkÇАС), то по определению внешней меры

m*(ЕÇА) £ 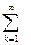m(AkÇА) и m*(ЕÇАС) £ 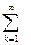m(AkÇАС).

Следовательно

m*(Е) > 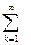m(Ak) – e = 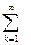m(AkÇА + АkÇAC) – e =

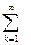= m(AkÇА) + 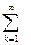m(АkÇAC) – e ³ m*(ЕÇА) + m*(ЕÇАС) – e.

В силу произвольности e, отсюда следует неравенство m*(Е) ³ m*(ЕÇА) + m*(ЕÇАС), которое доказывает утверждение.

Определение 26. В дальнейшем, полученную таким образом меру m, будем называть стандартным продолжением меры m или продолжением по Каратеодори.

Определение 27. m* -измеримое множество будем называть так же измеримым.

Теорема 11. Пусть m – стандартное продолжение на s-алгебру S меры m с полукольца P в X. Если В Ì X и для " e > 0 $ A ÎS: В ÌA и M(А) < e, то В ÎS и m(В) = 0.

Доказательство. В силу стандартности продолжения m найдется покрытие А (а значит и В) множествами из полукольца АkÎP такое, что M*(А) = m(А) £ Skm(Ak) < 2e. Последнее означает, что m*(В) = 0. Тогда для произвольного множества Е Ì Х выполняется вложение ЕÇВ Ì В и в силу монотонности внешней меры m*(ЕÇВ) £ m*(В) = 0, т.е. m*(ЕÇВ) = 0. Аналогично, ЕÇВС Ì Е и m*(Е) ³ m*(ЕÇВС) = m*(ЕÇВС) + m*(ЕÇВ). Последнее неравенство показывает измеримость В и так как m(В) = m*(В) = 0, то утверждение доказано.

Последняя теорема показывает, что стандартное распространение меры является полной мерой.

Теорема 12. (об измеримой оболочке). Пусть m - стандартное продолжение на s-алгебру S меры m с полукольца P в X. Если В Ì X, то найдется такое множество АÎS что В Ì А и m*(В) = m(А).

Доказательство. В случае, если m*(В) = ¥, в качестве А можно взять все Х. Пусть m*(В) < ¥. По определению внешней меры (теорема 8) найдутся такие множества BijÎP, что

, .

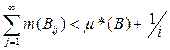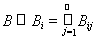
Поэтому множество 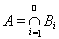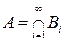будут измеримыми. В силу свойства монотонности и счетной полуаддитивности внешней меры

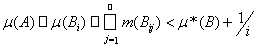
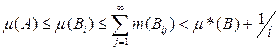
при всех i = 1, 2,… Перейдя к пределу в последнем неравенстве при i ®¥, получим неравенство m(А) £ m*(В). Так по построению В Ì А, то это неравенство доказывает теорему.

Множество А в данной теореме обладает двумя свойствами:

1) АÎS такое, что В Ì А и m*(В) = m(А);

2)

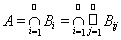
Множества, обладающие этими свойствами называются измеримой оболочкой для множества В.

Исследование, описанное в статье про 6. Измеримые множества, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 6. Измеримые множества и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ