4. Пространства Лебега и сопряженные к ним кратко

Привет, Вы узнаете о том , что такое 4. Пространства Лебега и сопряженные к ним, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 4. Пространства Лебега и сопряженные к ним , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Пусть задано измеримое пространство (X, S, m) с счетно-аддитивной меры m на множестве X и 1 £ р < ¥.

Определение 2. Множество всех измеримых функ­ций f: X ® R, у которых степень |f |p интегрируема на X, называется лебеговым пространством Lр(Х).

Элементами этого пространства Lр(Х) являются клас­сы эквивалентных функций.

Из неравенства Минковского вытекает, что Lр(Х) является линейным пространством. Норма в этом пространстве определяется по формуле:

.

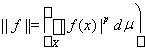
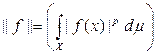Теорема 5. Пространства Lр(Х) при 1 £ р < ¥ являются банаховыми.

Доказательство. Вначале покажем, что Lр(Х) являет­ся нормированным пространством. Однородность нормы очевидно выполнена. Из неравенства Минковского вытекает ||f + g|| < ||f || + ||g|| – неравенство треугольника. Если ||f || = 0, то f(x) = 0 при п. в. х ÎХ (следствие 2 теоремы 5.4), и значит функция f ~ 0 эквивалентна нулю на X. Таким образом, все аксиомы нормы выполнены.

Докажем полноту пространства Lр(Х). Для каждой фундаментальной последовательности {fn} возьмем по­следовательность индексов n1 < n2 < ... так, что при всех i, j ³ nk выполняется неравенство ||fi – fj|| <2–k. Теперь заметим, что функция g(x) = ,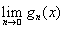

,

интегрируема в степени р. В самом деле, функции gn(x) образуют неубывающую последовательность gn ­ g при п ® ¥ и по неравенству треугольника

.

Следовательно, в силу теоремы о монотонной сходимо­сти функция g будет интегрируемой в степени р и значит конечной п. в. на множестве X. Отсюда ряд

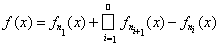
сходится абсолютно п. в. на X. Так как |f(x)|p £ gp(x), то функция f будет также интегрируемой в степени р.

Применяя лемму Фату (лемма 5.4) и неравенство треугольника, мы получим неравенство

.

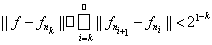
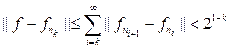Таким образом, = 0, т. е. существует предел у подпоследовательности { 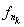}. Осталось заметить, что если последовательность {fn} фундаментальна в норми­рованном пространстве Lр(Х) и содержит сходящуюся подпоследовательность к функции f, то сама последо­вательность также является сходящейся в пространстве Lр(Х) и ее предел будет равен f (лемма 3.4).

Определение 3. Множество всех измеримых функ­ций f: X ® R, ограниченных на дополнении некоторого множества меры нуль, образует пространство L¥(X).

Элементами этого пространства L¥(X) являются клас­сы эквивалентных функций, называемые существенно ограниченными функциями на множестве X.

Из свойств измеримых функций вытекает, что L¥(X) есть линейное пространство. Об этом говорит сайт https://intellect.icu . Норма в нем по определению равна существенной верхней грани

.

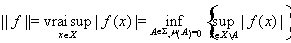
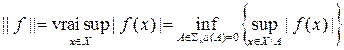Докажем, что нижняя грань в определении нормы до­стигается на некотором множестве меры нуль. Для этого выберем множества An ÎS меры нуль так, чтобы

,

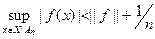и положим N(f) = 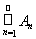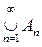. В силу счетной полуаддитив­ности меры множество N(f) имеет меру нуль и, значит, справедливо равенство .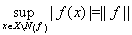

Отсюда нетрудно заметить, что сходимость в простран­стве L¥(X) совпадает с равномерной сходимостью на до­полнении некоторого множества меры нуль.

Теорема 6. Пространство существенно ограничен­ных функций L¥(X) есть банахово пространство.

Доказательство. Докажем вначале, что в пространстве L¥(X) выполняются аксиомы нормы. Свойство однород­ности нормы очевидно выполнено. Если ||f || = 0, то из сказанного выше вытекает, что f(x) = 0 п. в. на X и зна­чит функция f эквивалентна нулю.

Проверим неравенство треугольника. Пусть функции f, g Î L¥(X) и множество A = N(f)ÈN(g), тогда

.

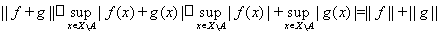
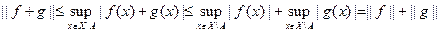Докажем полноту пространства L¥(X). Для этого рас­смотрим фундаментальную последовательность {f n} и определим множество D = 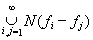меры m(D) = 0. Поскольку имеет место равенство

,

то на множестве X\D последовательность {f n} будет ограниченной и фундаментальной в чебышевской метри­ке. В силу полноты пространства ограниченных функций M(X\D} существует равномерный предел 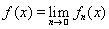на множестве X\D. Положим f = 0 на D, тогда функция f ограничена и измерима на множестве X. При этом, в си­лу равномерной сходимости, предел 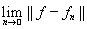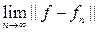= 0 в метрике L¥(X).

Пусть задано измеримое пространство (X, å, m) с счетно-аддитивной мерой m. Обозначим через Á(Х) множество всех простых интегрируемых функций на X и будем предполагать, что Х имеет s-конечную меру.

Теорема 7. Сопряженное пространство Lр*(X) изометрично пространству Lq(X), где число q = p/(p—1) в случае 1 < р < ¥ и q = ¥ в случае р = 1. При этом каждый ограниченный функционал aÎ Lр*(X) пред­ставляется интегралом Лебега:

,

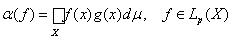
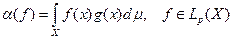где g Î Lq(X) и норма функционала равна ||a|| = ||g||q (норме функции g в пространстве Lq(X)).

Доказательство. Рассмотрим функцию j(А) = a(cА) из­меримого множества А Îå конечной меры. В силу свой­ства линейности функционала a эта функция является конечно-аддитивной. Поскольку по определению нормы функционала а имеет место неравенство |j(A)| = |a(cA)| £ ||a||×||cA|| = ||a||m1/p(A), то функция j(А) – абсолютно непрерывна. По теореме Радона-Никодима существует интегрируемая функция g на каждом измеримом множестве А Îå конечной меры такая, что имеет место равенство j(А) = .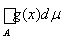

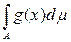Каждая простая функция h ÎÁ(Х) является линей­ной комбинацией характеристических функций. Поэтому в силу линейности интеграла и функционала a

h ÎÁ(Х).

Возьмем теперь простую функцию h ÎÁ(Х) такую, что 0 £ h £ |g|. Так как функция hq–1´sgn(g(x)) измерима и огра­ничена, то она является равномерным пределом последо­вательности простых функций hn ÎÁ(Х). Поэтому

= .

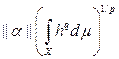Откуда и из определения интеграла Лебега вытекает, что ||g||q £ ||a|| в случае р > 1.

В случае р = 1 допустим, что при некотором e > 0 мно­жество Е Ì{xÎA: |g(x)| > ||a|| + e} имеет конечную и положительную меру. Полагая h(х) = cE ´sgn(g(x)), имеем

.

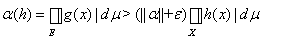
Это противоречит определению нормы функционала a. Следовательно, ||g||¥ £ ||a|| в случае р = 1.

Поскольку каждая интегрируемая функция f ÎLp(X) может быть представлена в виде предела простых ин­тегрируемых функций hn ÎÁ(Х) и в силу неравенства Гельдера мы получим

,

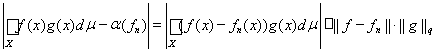
то из непрерывности функционала a вытекает

a(f ) = –

указанное представление. Применяя теперь к этому пред­ставлению неравенство Гельдера

,

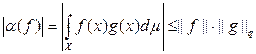заключаем, что норма функционала ||a|| = ||g||q.

Пример 7. Пусть 1 £ р < ¥ и lр пространство всех последовательностей из примера 6.3. Заметим, что lр есть частный случай пространства Lp(X), где X = N есть множество натуральных чисел и мера m(А) равна количеству натуральных чисел множества А Ì N.

По доказанному ранее lp является банаховым простран­ством. Следующая теорема есть частный случай теоремы для пространства Lp(X).

Теорема 8. Если 1 £ р < ¥, то сопряженное пространство (lp)* изометрично пространству lq, где число q = р/(р – 1) в случае 1 < р < ¥ и q = ¥ в случае р = 1

Исследование, описанное в статье про 4. Пространства Лебега и сопряженные к ним, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 4. Пространства Лебега и сопряженные к ним и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ

Из статьи мы узнали кратко, но содержательно про