2. Системы множеств в евклидовом пространстве кратко

Привет, Вы узнаете о том , что такое 2. Системы множеств в евклидовом пространстве, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 2. Системы множеств в евклидовом пространстве , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Определение 7. Пусть заданы n пар вещественных чисел аi и bi, где i = 1,..., n, так, что ai < bi "i. При этом мы допускаем, что некоторые из этих чисел могут быть несоб­ственными, т.е. возможно, что ai = - ¥ и bi = +¥ при некоторых i. Множество D0 всех точек х = (x1,..., xn) Ρn, координаты которых удовлетворяют неравенству ai < xi < bi, i = 1, …, n, называется открытым n-мерным параллелепипедом.

Ранее было показано (пример 1.5), что открытые параллелепипеды образуют базу топологии в Rn.

Определение 8. Множество D* всех точек х Î ¡n, координаты которых удовлетво­ряют неравенству аi £ xi £ bi, i = 1,..., n, называется замкнутым n-мерным параллеле­пипедом.

Если рассматривать Rn с топологией, порожденной метрикой Евклида, то открытый параллелепипед является открытым множеством, замкнутый – замкнутым множеством (проверьте).

Определение 9. Параллелепипед D – это любое множество, удовлетворяющее условию: D0 Ì Δ Ì D*. Далее мы его будем обозначать так D{a1, b1;...; аn, bn}.

Определение 10. Если - ¥ < аi < bi < + ¥ при всех i, то будем говорить, что D -параллелепипед с конечными ребрами. Об этом говорит сайт https://intellect.icu . Если же хоть одна из величин аi и bi является бесконечной, то будем говорить, что D имеет бесконечное ребро.

Определение 11. Будем говорить, что два параллелепипеда дизъюнктны, если у них нет общих вну­тренних точек.

Определение 12. Объемом n-мерного параллелепипеда D{a1, b1;...; аn, bn} называется: VD =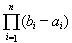

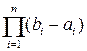
Он равен + ¥, если у параллелепипеда есть бесконечное ребро.

Определение 13. Параллелепипед D{a1, b1;...; аn, bn} называется (n-мерной) ячейкой, если он состоит из всех точек х, координаты которых удовлетворяют неравенствам аi £ xi < bi, где i = 1,..., n.

Пусть P1 и P2 – полукольца на множествах Х1 и Х2, соответственно. Построим систему множеств P = P1´P2, т.е. А´В ÎP тогда и только тогда, когда АÎP1 и ВÎP2.

Лемма 1. Система P является полукольцом в Х1´Х2.

Доказательство. 1) Æ = Æ´ÆÎP.

2) Если А1´В1, А2´В2ÎP, то А1´В1 Ç А2´В2 = (А1ÇА2)´(В1ÇВ2)Î P (в силу свойств полуколец P1 и P2).

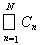
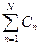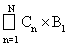
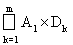
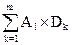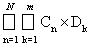
3) Пусть А1´В1, А2´В2ÎP и А1´В1 Ì А2´В2, последнее влечет вложения множеств А1 Ì А2 и В1 Ì В2. В силу свойств полуколец P1 и P2 найдутся множества Сn ÎP1 и DkÎ P2, такие, что А2 = А1 + и В2 = В1 + . В силу свойств произведения дизъюнктных множеств получаем представление А2´В2 = А1´В1 + + + , что эквивалентно третьему условию в определении полукольца.

Рассмотрим ячейки на числовой прямой, т.е. систему P1 промежутков вида [a; b).

Теорема 3. Система P1 промежутков вида [a; b) образует полукольцо пространства R1.

Доказательство. 1) Справедливо Æ = [a; a).

2) Пусть [a1; b1), [a2; b2). Тогда нетрудно видеть, что пересечение этих промежутков либо пусто, либо [a1; b1) Ç [a2; b2) = [max{a1, a2}; min{b1; b2})(сделайте рисунок).

3) Пусть [a1; b1) Ì [a2; b2). Тогда нетрудно видеть, что выполняется равенство [a2; b2) = [a2; a1) + [a1; b1) +[b1; b2), что доказывает последнее свойство полукольца.

Следствие. Система всех ячеек пространства Rn образует полукольцо P.

Утверждение следствия легко вытекает из теоремы и леммы 1.

Исследование, описанное в статье про 2. Системы множеств в евклидовом пространстве, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 2. Системы множеств в евклидовом пространстве и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ