2. Теорема Шаудера о полной непрерывности сопряженного оператора. Уравнения первого и второго рода с вполне непрерывными операторами. Теорема о замкнутости области значений оператора кратко

Привет, Вы узнаете о том , что такое 2. Теорема Шаудера о полной непрерывности сопряженного оператора. Уравнения первого и второго рода с вполне непрерывными операторами. Теорема о замкнутости области значений оператора, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 2. Теорема Шаудера о полной непрерывности сопряженного оператора. Уравнения первого и второго рода с вполне непрерывными операторами. Теорема о замкнутости области значений оператора , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Оказывается, АÎL(X, Y) и сопря­женный к нему оператор A*Î L(Y*, X*) одновременно вполне непрерывны или нет. Точнее, имеет место следующая теорема Шаудера.

Теорема 3 (Шаудера). Пусть АÎL(X, Y), где Y – полное. Оператор А вполне непрерывен тогда и только тогда, когда А* вполне не­прерывен.

Необходимость. Пусть S и S* – замкнутые единичные шары с центром в начале координат пространств X и Y* соответ­ственно. Рассмотрим АÎK(X, Y). Возьмем произвольную последовательность функционалов {fn} Î S* и рассмотрим последовательность функций jn (y) = fn(y), n=1, 2, ... На любом ограниченном в Y множестве эти функции равно­мерно ограничены (по n), так как |jn (y)| = |fn(y)| £ ||fn||×||y|| £ ||y|| и равностепенно непрерывны: |jn (y1) - jn (y2)| = |jn (y1 - y2)| = |fn(y1 – y2)| £ ||fn||×||y1 – y2||.

Будем рассматривать {jn (y)} на множестве AS, которое компактно (ведь А вполне непрерывен) и замкнуто. По теореме Арцела найдется подпоследовательность {jnk(Ax)} = {A*fnk(x)}, сходящаяся на S равномерно. Это означает, что {A*fnk} сходится в метрике X*. Следовательно, А* вполне непрерывен.

Достаточность. Пусть А* вполне непрерывен. Тогда по доказанному выше А** = (А*)* также вполне непрерывен. Пусть S** – замкнутый единичный шар в X**. Множество A**S** Ì Y** относительно компактно. Так как пространство Y Ì Y**, то в соответствии с этим вложением AS Ì A**S** и, значит, AS относительно компактно в Y. Это и означает, что А вполне непрерывен. Теорема доказана.

Пусть А вполне непрерывный линейный оператор, действующий в банаховом пространстве X. Об этом говорит сайт https://intellect.icu . Линейное уравнение вида (у Î Х)

х - Ах = у (3)

будем называть уравнением 2-го рода. Линейное уравнение Ах = у с вполне непрерывным оператором А будем называть уравнением 1-го рода. Как ни странно, теория линейных уравнений 2-го рода (3) намного проще по сравнению с теорией уравнений 1-го рода.

Перейдем к ее изложению. Наряду с уравнением (3) будем рассматривать соответствующее ему однородное уравнение

z – Az = 0, (4)

а также сопряженное уравнение

f – A*f = w (3*)

и сопряженное однородное уравнение

f – A*f = 0 (4*)

Заметим, согласно теореме Шаудера оператор A* вполне непрерывен, так что все уравнения (3), (3*), (4), (4*) являются уравнениями 2-го рода. Докажем сначала следующее вспомогательное предложение.

Теорема 4. Пусть А – линейный вполне непрерывный опе­ратор. Тогда множества значений операторов I – А и I – А* замкнуты и, значит, являются подпространствами в X и в X* со­ответственно.

Доказательство. Пусть {уn} принадлежит R(I – A) – множеству значений оператора I – А. Тогда най­дутся xn Î X такие, что хn – Ахn = уn. Пусть уn ® у0 при n ® ¥. Покажем, что y0 Î R(I – A). Рассмотрим ряд случаев. Если {хn} ограничена, то {Ахn} относительно компактна, откуда следует, что {хn} также относительно компактна. Достаточно заметить, что хn = уn + Ахn, где {yn} сходится, а {Ахn} относительно компактна. Вследствие компактно­сти из {хn} можно выделить {хn(k)} – подпоследовательность, сходящуюся к х0; тогда, переходя к пределу при n(k) ® ¥ в ра­венстве хn(k) – Ахn(k) = уn(k) получим вследствие непрерывности А, что х0 – Ах0 = у0, т. е. у0 Î R (I – А).

Если {хn} не ограничена, то поступим следующим образом. Пусть N – подпространство нулей оператора I – A, т. е. мно­жество всех решений уравнений (4). Введем расстояние dn = d(xn, N) = infz Î N ||xn – z||. Согласно определению нижней грани в N найдется элемент zn такой, что dn £ ||xn – zn|| £ (1 + 1/n)dn. Далее, (I – A) (хn – zn) = yn. Если {dn} ограничена, то, как и выше, с заменой хn на xn – zn получаем, что y0 Î R(I – A).

Оказывается, случай неограниченности {dn} невозможен. В самом деле, если {dn} не ограничена, то, переходя, если нуж­но, к подпоследовательности, можно считать, что dn ® ¥, при n ® ¥. Рассмотрим элементы

.

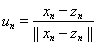
Тогда ||un|| = 1 и (I – A)un = 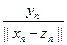® 0, n ® ¥, так как

.

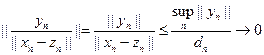Как и выше, отсюда следует, что найдется подпоследовательность иn(k) ® u0, причем u0ÎN. Но xn(k) – zn(k) – || xn(k) – zn(k)||u0 = (un(k) – u0) || xn(k) – zn(k)||. Причем zn(k) + || xn(k) – zn(k)||u0 Î N. Следовательно, по неравенству (3) имеем

||un(k) – u0||(1 + 1/nk)dn(k) ³ || (un(k) – u0)||xn(k) – zn(k)|| || =

= ||xn(k) – {zn(k) + ||xn(k) – zn(k)||u0}|| ³ dn(k)

откуда ||un(k) – u0|| ³ n(k)/(n(k) + 1), а это противоречит тому, что ||un(k) – u0|| ® 0 при n(k) ® ¥. Итак, {dn} ограничена и замкнутость R(I – A) доказана. Замкнутость R(I – A*) является следствием вышеизложенного, ибо А* также вполне непрерывен. Теорема доказана

Исследование, описанное в статье про 2. Теорема Шаудера о полной непрерывности сопряженного оператора. Уравнения первого и второго рода с вполне непрерывными операторами. Теорема о замкнутости области значений оператора, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 2. Теорема Шаудера о полной непрерывности сопряженного оператора. Уравнения первого и второго рода с вполне непрерывными операторами. Теорема о замкнутости области значений оператора и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ