Привет, Вы узнаете о том , что такое теорема гильберта-шмидта, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое теорема гильберта-шмидта , настоятельно рекомендую прочитать все из категории Функциональный анализ.

5. Существование собственного значения у вполне непрерывного оператора в гильбертовом пространстве.

Наибольшее и наименьшее собственные значения.

Спектральное разложение самосопряженных операторов.

теорема гильберта-шмидта о разложении по собственным векторам

Мы переходим теперь к фундаментальной теореме о симметричных вполне непрерывных операторах.

Теорема 8. (Гильберта-Шмидта). В гильбертовом сепарабельном пространстве всякий симметричный вполне непрерывный оператор обладает полной ортогональной системой собственных векторов.

Доказательство этой теоремы проведем в несколько этапов.

Лемма 7. Если 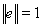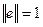и А – симметричный оператор, то

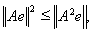
причем знак равенства возможен только в случае, когда е есть собственный вектор оператора 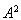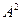с собственным значением

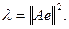
Доказательство. В силу симметрии оператора и неравенства Коши – Буняковского имеем:

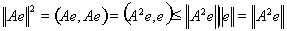
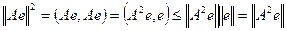(12)

Неравенство Коши – Буняковского обращается в равенство, лишь когда фигурирующие в нем векторы коллинеарные, поэтому в случае равенства имеем 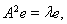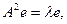т.е. есть собственный вектор оператора А2. Подставляя полученное выражение в (12), находим :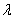

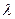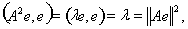
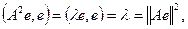
Лемма доказана.

Назовем максимальным вектором ограниченного оператора А такой единичный вектор 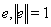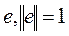на котором величина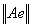 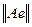достигает своего наибольшего значения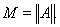 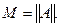Вообще говоря, не у всякого ограниченного оператора существует максимальный вектор.

Лемма 8. Симметричный вполне непрерывный оператор обладает максимальным вектором.

Доказательство. Выберем последовательность 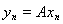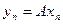, где 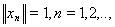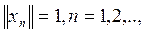так, чтобы иметь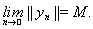 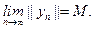Из последовательности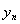 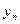можно выделить в силу полной непрерывности А, сходящуюся подпоследовательность, удалив лишние векторы и исправив нумерацию, можно считать, что сама последовательность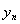 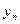сходится при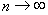 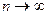; пусть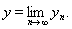 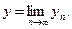В силу непрерывности нормы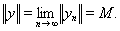 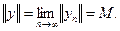Покажем, что вектор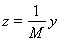 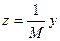является исходным максимальным вектором. Прежде всего, в силу непрерывности оператора А имеем:

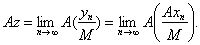
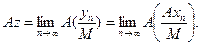
Векторы 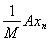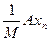принадлежат единичному шару, и поэтому векторы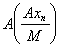 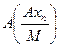по длине не превосходят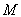 . Применяя лемму 7, получаем:

.

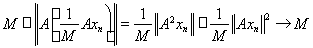
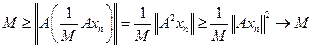Откуда вытекает, что

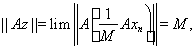
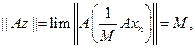
т.е. 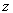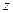есть максимальный вектор оператора А. Лемма доказана.

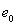
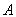
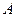Лемма 9. Если есть максимальный вектор для симметричного оператора , то 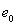является собственным вектором для оператора 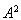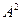с собственным значением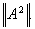

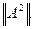
Доказательство. По лемме 7 и по определению нормы оператора имеем:

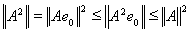
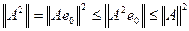
откуда следует, что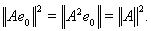

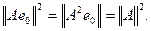
В силу леммы 7 вектор 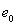есть собственный вектор оператора 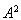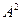с собственным значением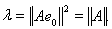 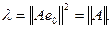Лемма доказана.

Лемма 10. Если оператор 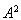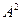обладает собственным вектором с собственным значением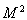 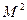, то оператор А имеет собственный вектор с собственным значением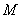 или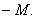

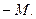
Доказательство. Равенство 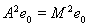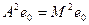можно записать в виде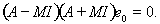

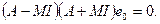
Допустим, что 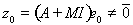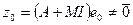. Тогда из условия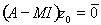 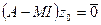или, что тоже,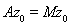 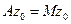вытекает, что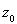 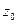есть собственный вектор оператора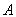 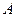с собственным значением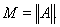 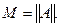Если же , то 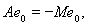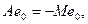и тогда вектор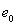 есть собственный вектор оператора А собственным значением 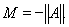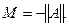Лемма доказана.

Леммы 7-10 показывают, что всякий симметричный вполне непрерывный оператор А обладает собственным вектором с собственным значением 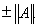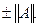Покажем теперь, что из собственных векторов оператора А можно построить ортогональную систему в пространстве Н.

Лемма 6 позволяет сделать определенные выводы относительно совокупности всех собственных векторов и собственных значений оператора А. Об этом говорит сайт https://intellect.icu . Рассмотрим на вещественной оси множество всех собственных значений оператора А. В силу леммы 6, существует лишь конечное число собственных значений, превосходящих по абсолютной величине данное положительное число 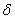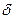, поэтому, если собственных значений бесконечное (очевидно, счетное) множество, то они образуют последовательность, сходящуюся к нулю. Следовательно, мы можем занумеровать натуральными числами все собственные значения в порядке убывания абсолютной величины. Условимся, что при этом мы будем каждое собственное значение снабжать столькими последовательными номерами, какова размерность соответствующего собственного подпространства (эта размерность называется кратностью этого собственного значения). В таком случае последовательность ненулевых собственных значений оператора А

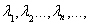
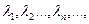
мы можем сопоставить последовательность собственных векторов 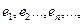причем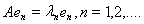 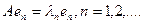Можно считать, что векторы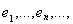 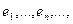взаимно ортогональны и нормированы. В самом деле, если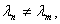 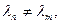то ортогональность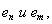 выполняется в силу леммы 5; если же 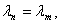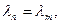то в пределах конечного собственного подпространства, отвечающего собственному значению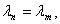 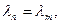мы всегда можем провести ортогонализацию. Нормировка всех полученных векторов завершает построение.

Покажем теперь, что каждый вектор 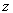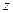, ортогональный всем построенным векторам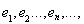 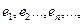переводится оператором А в нуль.

Лемма 11. Пусть 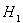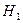– подпространство в гильбертовом пространстве Н, инвариантное относительно симметричного оператора А (т.е. каждый вектор подпространства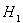 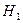переводится оператором А в вектор этого же пространства). Тогда ортогональное дополнение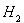 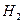подпространства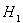 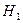также инвариантно относительно оператора А.

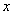
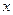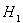
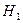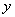
Доказательство. Пусть – любой вектор из подпространства , 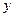– любой вектор из подпространства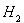 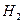. По условию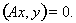 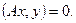Тогда в силу симметрии оператора А следует, что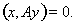 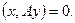Это означает, что вектор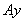 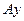ортогонален любому вектору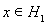 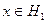и, следовательно,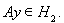 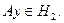Лемма доказана.

Теперь рассмотрим совокупность Р всех векторов 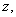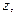ортогональных всем построенным векторам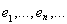 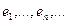Это совокупность Р является замкнутым подпространством как ортогональное дополнение к подпространству L, порожденному ортогональной системой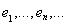 Поскольку L, очевидно, инвариантно относительно оператора А, то его ортогональное дополнение P (по лемме 11) также инвариантно относительно оператора A. Обозначим через M(P) точную верхнюю границу значений 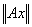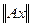на единичной сфере подпространства P. В силу лемм 9 и 10, в подпространстве Р имеется собственный вектор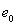 с собственным значением 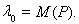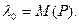Но по самому построению подпространства Р оно не может содержать ни одного собственного вектора с ненулевым собственным значением. Отсюда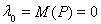 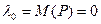; но это означает, что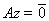 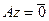для любого вектора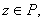 что и требовалось доказать.

Каждый вектор 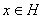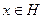может быть представлен в виде суммы

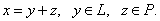
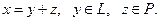
Вектор у можно далее разложить в ряд Фурье по системе 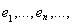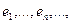полной в пространстве L; вектор z, по доказанному, оператором A переводится в нулевой вектор. Мы получили следующую основную теорему:

Терема 9. В гильбертовом пространстве 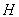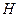, в котором задан симметричный вполне непрерывный оператор A, каждый вектор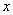 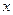может быть представлен в виде ортогональной суммы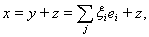 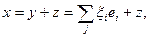где 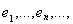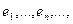(конечная или бесконечная) система собственных векторов оператора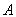 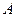с ненулевыми собственными значениями и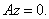

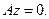
Из этой теоремы вытекает и теорема Гильберта. Действительно, в сепарабельном гильбертовом пространстве H подпространство P также сепарабельно и в нем можно выбрать полную ортогональную систему 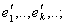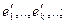вместе с уже построенными векторами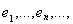 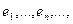получается полная ортогональная система в всем пространстве H. Каждый из векторов этой системы является собственным вектором оператора A: векторы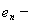 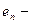с собственными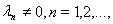 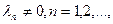а векторы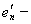 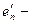с собственным значением 0. Тем самым теорема Гильберта доказана.

Из теоремы Гильберта следует, что 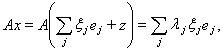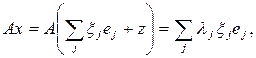т.е. любой вектор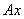 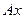, где 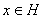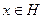, допускает разложение по собственным векторам оператора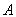 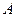с ненулевыми собственными значениями.

Задачи

1. Доказать следующие утверждения:

А) любой линейный оператор A: Rn®Rm вполне непрерывен;

Б) любой линейный оператор A: E1®E2 вполне непрерывен, если E1 – конечномерное пространство;

В) любой ограниченный линейный оператор A: E1®E2 вполне непрерывен, если E2 – конечномерное пространство;

Г) линейный ограниченный оператор, образ которого лежит в конечномерном пространстве, вполне непрерывен.

2. Являются ли вполне непрерывными следующие операторы в пространстве C[0, 1]? В пространстве L2[0, 1]?

1) ;

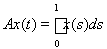
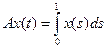2) ;

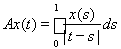
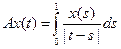3) ;

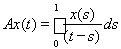
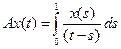4) ;

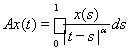
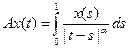5) ;

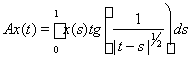
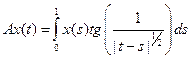6) ;

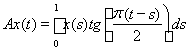
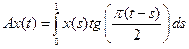7) ;

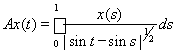
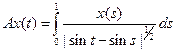8) ;

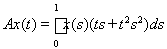
9) ;

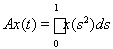
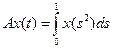10) Ax(t)=x(t2).

3. Имеет ли оператор 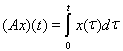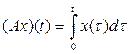собственные значения в пространстве ?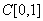

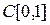4. Показать, что для уравнения 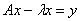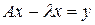, где 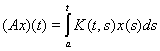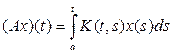– оператор Вольтерра, а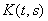 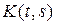непрерывно для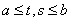 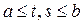, все значения параметра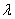 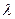регулярны.

Показать, что если значение параметра l является регулярным для оператора, то оно будет регулярным и для оператора А + В, когда 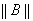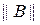достаточно мала.

5. Показать, что всякий вполне непрерывный оператор в сепарабельном гильбертовом пространстве Н есть предел операторов, отображающих все пространство на конечномерное подпространство.

Указание: можно считать, что 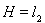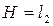. Если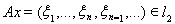 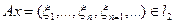, то положим .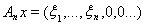

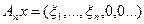6. Показать, что оператор А в сепарабельном гильбертовом пространстве, заданный в ортонормальном базисе 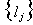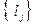матрицей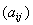 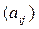по формулам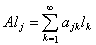 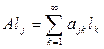вполне непрерывен, если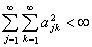

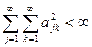
Указание: смотри задачу 5.

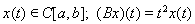
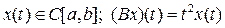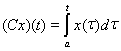
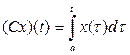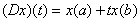
7. Положим для , , 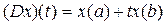. Какие из этих операторов вполне непрерывны?

8. Для 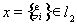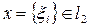, положим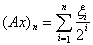 , показать, что А – вполне непрерывный оператор.

9. Каковы собственные функции интегрального оператора Фредгольма с ядром 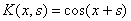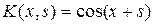в промежутках а)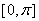 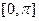, б) ?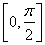

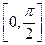10. Решить уравнение .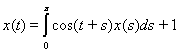

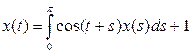11. В пространстве C[0, 1] рассмотрим оператор

.

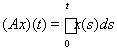
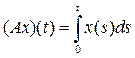Найти спектр и резольвенту оператора А.

12. В вещественном линейном пространстве C[-p, p] найти собственные значения и собственные вектора операторов

а) (Ax)(t) = x(-t);

b) .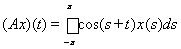

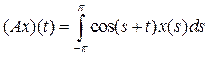Имеют ли в этом пространстве данные операторы непрерывный спектр? Построить резольвенты на множестве регулярных значений каждого оператора.

13. В комплексном пространстве C[0, 1] рассмотрим оператор (Ах)(t) = x(0) + tx(1). Найти точечный и непрерывный спектры оператора А и построить резольвенту на множестве регулярных значений.

14. В пространстве C[0, 2p] рассмотрим оператор (Ах)(t) = eittx(t). Доказать, что спектр оператора А есть множество {l ÎC: |l| = 1}, причем ни одна точка спектра не является собственным числом.

15. Найти спектр и резольвенту оператора А в пространстве L2[-1, 1]

.

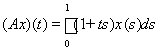
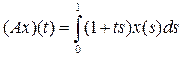16. Какой должна быть функция jÎС[a, b], чтобы оператор умножения А: С[a, b] ® С[a, b], определенный с помощью равенства (Ах)(t) = j(t)×x(t) был вполне непрерывным.

17. Найти спектр и собственные значения оператора умножения на фиксированную непрерывную функцию в пространстве C[a, b].

18. Найти спектр оператора А в пространстве L2(R):

.

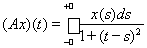
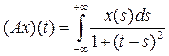19. Пусть число p > 1 и q – ему сопряженное, т.е. 1/p + 1/q = 1. Рассмотрим оператор А: lp ® lq, который определяется формулой

,

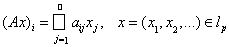
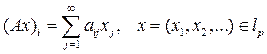где числовая матрица 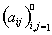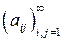такая, что двойной ряд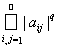 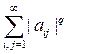сходится. Доказать, что оператор А вполне непрерывен.

20. Рассмотрим оператор А: lp ® lq, который определяется формулой

Ах = (l1х1, l2х2, …), х = (х1, х2, …)

где lk – заданная последовательность чисел, k =1, 2, … Какова должна быть последовательность этих чисел, чтобы оператор А был вполне непрерывен.

21. Пусть в гильбертовом пространстве Н задан линейный ограниченный оператор А такой, что А*А является вполне непрерывным оператором в Н. Доказать, что оператор А вполне непрерывен?

Исследование, описанное в статье про теорема гильберта-шмидта, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое теорема гильберта-шмидта и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ