4. Мера и ее простейшие свойства. Мера в евклидовом пространстве кратко

Привет, Вы узнаете о том , что такое 4. Мера и ее простейшие свойства. Мера в евклидовом пространстве, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 4. Мера и ее простейшие свойства. Мера в евклидовом пространстве , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Определение 17. Пусть X - любое множество. Мерой в X называется вещественнозначная неотрицательная счетно-аддитивная функция m, заданная на некотором полукольце P подмножеств множества X.

Определение 18. Мера m называется конечной, если m(А) < + ¥ для " А Î P.

Определение 19. Мера m называется s-конечной, если " А Î P $ такие Аn Î P (n = 1, 2,...), что А Ì 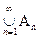и мера m(Аn) < + ¥ для " n.

Определение 20. Пусть m – произвольная мера в X, заданная на каком-то полукольце P. Она называется полной, если из того, что А Î P, m(А) = 0 и Е Ì А вытекает, что Е Î P.

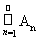
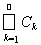
Лемма 3. Если P - полукольцо, An ÎP, A = ÎP, то = , где Сk Î P, при этом для каждого k существует n(k) такое, что Сk Ì An(k).

Доказательство. Очевидно, что

А = А1È[(А\А1)ÇA2]È[(A\A1)Ç(A\A2)ÇA3]…[ 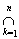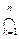(A\Ak)ÇAn+1]… (1)

Заметим, сразу, что все множества, стоящие в квадратных скобках дизъюнктны между собой по построению. По условиям полукольца А\Аk = , где Сki Î P. Следовательно

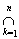
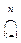(A\Ak)ÇAn+1 =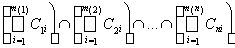 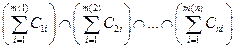ÇAn+1 =

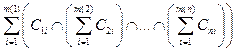= ÇAn+1 =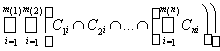 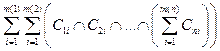ÇAn+1 =

= .

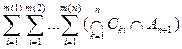Стоящие в последних скобках множества по определению полукольца принадлежат ему и все между собой дизъюнктны. Об этом говорит сайт https://intellect.icu . Подставив полученное равенство в (1) получим доказываемое.

Теорема 6. Пусть X – любое множество с полукольцом P и неотрицательной конечно-аддитивной функцией множеств m на этом полукольце. Справедливы следующие свойства:

1. m(Æ) = 0;

2. Если А, В Î P и А Ì В, то m(A) £ m(B) (монотонность меры);

Если m является мерой (т.е. обладает еще свойством счетной аддитивности), то

3. Если А, An ÎP и А Ì 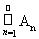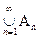, то m(A) £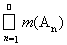 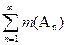(полуаддитивность меры)

Доказательство. 1) Легко вытекает из свойства аддитивности и неотрицательности, так как m(Æ) = m(ÆÈÆ) = m(Æ) + m(Æ) = 2m(Æ).

2) В силу свойств полукольца найдется конечный набор множеств Сk ÎP таких, что В = А + 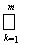Сk.Тогда из аддитивности m вытекает m(B) = m(A) + m(Сk), откуда и неотрицательности m уже легко следует нужное неравенство.

3) Из условий теоремы получаем представление А = 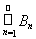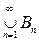, где Вn = AÇAnÎP. Воспользуемся теперь леммой: А = , где СkÎP. Отметим, что в силу леммы

,

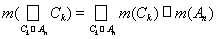
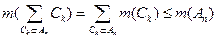при этом одно и тоже Сk может полностью попасть в разные Аn (но, что очень важно в силу леммы, хотя бы в одно из них обязательно попадает полностью). Отсюда уже легко следует, что

m(А) = .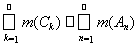

Теорема 7. Функция V, заданная на полукольце P ячеек в Rn и равная для каждой ячейки ее объему – s-конечная мера в Rn.

Доказательство. Практически в доказательстве нуждается только счетная аддитивность введенной функции, так как конечная аддитивность очевидна. Пусть D{a1, b1;...; аn, bn} = 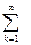D{c1(k), d1(k);…; cn(k), dn(k)}. Далее предполагаем, что все ячейки, входящие в сумму имеют конечные ребра, в противном случае равенство очевидно. Ясно, что D{c1(k), d1(k);…; cn(k), dn(k)} Ì D {a1, b1;...; аn, bn} для любого m. В силу монотонности и аддитивности функции множеств V выполняется неравенство V( D{c1(k), d1(k);…; cn(k), dn(k)}) = 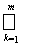V(D{c1(k), d1(k);…; cn(k), dn(k)}) £ V(D {a1, b1;...; аn, bn}) для любого m. Предельным переходом по m получаем неравенство

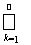
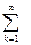V(D{c1(k), d1(k);…; cn(k), dn(k)}) £ V(D {a1, b1;...; аn, bn}).

Докажем противоположное неравенство. Рассмотрим систему открытых параллелепипедов {D0{c1(k) - e/2k, d1(k) + e/2k; …..; cn(k) - e/2k, dn(k) + e/2k}}, где e произвольное положительное число. Данная система покрывает замкнутый параллелепипед D*{a1, b1;...; аn, bn}. Так как последний является компактным множеством (он ограничен и замкнут), то из этого покрытия можно выделить конечное подпокрытие:

D*{a1, b1;...; аn, bn} Ì 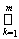D0{c1(k) - e/2k, d1(k) + e/2k; …..; cn(k) - e/2k, dn(k) + e/2k}

(без ограничения общности мы предположили, что нужное конечное покрытие находится в начале). Тогда

V(D*{a1, b1;...; аn, bn}) £

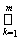
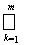
£ V( D0{c1(k) - e/2k, d1(k) + e/2k; …..; cn(k) - e/2k, dn(k) + e/2k}) £

£ V(D0{c1(k) - e/2k, d1(k) + e/2k; …..; cn(k) - e/2k, dn(k) + e/2k}) £

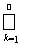
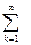£ V(D0{c1(k) - e/2k, d1(k) + e/2k; …..; cn(k) - e/2k, dn(k) + e/2k}) £

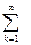£ V(D0{c1(k), d1(k); …..; cn(k), dn(k)}) + 2nV(D*{a1, b1;...; аn, bn}) 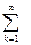e/2k =

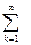= V(D0{c1(k), d1(k); …..; cn(k), dn(k)}) + 2nV(D*{a1, b1;...; аn, bn})e.

В силу произвольности e последнее доказывает противоположное неравенство.

Исследование, описанное в статье про 4. Мера и ее простейшие свойства. Мера в евклидовом пространстве, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 4. Мера и ее простейшие свойства. Мера в евклидовом пространстве и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ