1. Вполне непрерывные операторы и их свойства. Операторы Фредгольма и Гильберта-Шмидта кратко

Привет, Вы узнаете о том , что такое 1. Вполне непрерывные операторы и их свойства. Операторы Фредгольма и Гильберта-Шмидта, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 1. Вполне непрерывные операторы и их свойства. Операторы Фредгольма и Гильберта-Шмидта , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Определение 1. Линейный оператор А, действующий из линейного нормированного пространства X в линейное нормированное пространство Y, называется вполне непрерывным, если он отображает всякое ограниченное множество пространства X в относительно компактное множество пространства Y.

Теорема 1. Всякий вполне непрерывный оператор является ограниченным.

Доказательство. Так как А вполне непрерывен, то образ единичного шара из X будет относительно компактное множество в Y, а любое относительно компактное множество ограничено, что означает ограниченность оператора А. Теорема доказана.

Если y = Ax – произвольный линейный (ограниченный) оператор, то образ любого ограниченного множества также ограничен. Поэтому, если пространство Y таково, что в нем всякое ограниченное множество относительно компактно, то и всякий линейный оператор, отображающий X в Y, будет вполне непрерывен. В частности, это заключение справедливо для линейных операторов и для линейных функционалов, совокупность значений которых конечномерна. Однако, в общем случае, при произвольных X и Y , можно лишь утверждать, что вполне непрерывные операторы составляют часть класса линейных операторов. Например, в пространстве l2 множество всех координационных ортов ограничено, но из него нельзя выделить сходящийся последовательности, так как расстояние между любыми двумя различными ортами равно 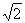. Из этого следует, что тождественный оператор в l2 не будет вполне непрерывным. Также не является вполне непрерывным тождественный оператор I в пространстве C[0, 1]. В самом деле, оператор I переводит ограниченную последовательность xn(t) = tn в себя, а эта последовательность не компактна в смысле равномерной сходимости.

Пример 1. Пусть Ax = 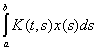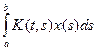, где K(t, s) непрерывное в квадрате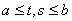 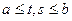ядро оператора. Тогда оператор А действует в C[a, b] и вполне непрерывен. То, что оператор A линеен и действует в C[a, b] было доказано прежде. Требуется доказать, что для любого ограниченного множества 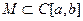множество A(M) компактно. Рассмотрим функции вида

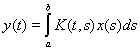
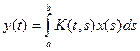
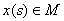
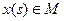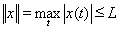
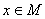
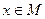где . Пусть для любого . Имеем

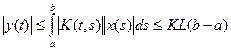, где

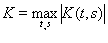
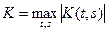. Таким образом, функции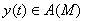 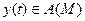равномерно ограничены. Далее,

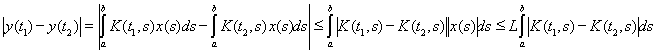
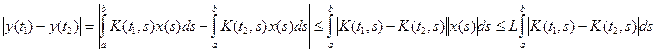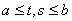
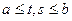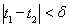
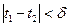Ядро K(t,s), как непрерывное в замкнутом квадрате , по теореме Кантора равномерно непрерывно в нем. Об этом говорит сайт https://intellect.icu . Поэтому всякий раз, когда независимо от положения точек (t1,s) и (t2,s) в квадрате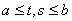 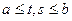. Но тогда

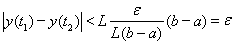
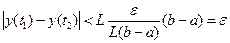
всякий раз, когда 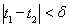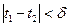независимо от выбора функции y(t) в множестве A(M) и от положения точек t1 и t2 на отрезке [a, b], что означает равностепенную непрерывность функций множества A(M).

Таким образом, функции множества A(M) равномерно ограничены и равностепенно непрерывны, следовательно, по теореме Арцела множество A(M) относительно компактно, что и требовалось доказать.

Лемма 1. Пусть А – вполне непрерывный оператор, отображающий банахово пространство в себя, и В – произвольный линейный непрерывный оператор, действующий в том же пространстве. Тогда АВ и ВА – вполне непрерывные операторы.

Доказательство. В самом деле, оператор В преобразует произвольное ограниченное множество M в ограниченное множество В(М) , и это множество оператор А преобразует в относительно компактное множество А(В(М)). Следовательно, оператор АВ переводит любое ограниченное множество в относительно компактное и поэтому вполне непрерывен. Аналогично показывается, что и оператор ВА вполне непрерывен.

Нетрудно видеть, что если операторы A и B вполне непрерывны, то 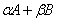также будет вполне непрерывным оператором.

Таким образом, вполне непрерывные операторы в пространстве линейных операторов, преобразующих X в Y, образуют линейное многообразие.

Следующая теорема показывает, что при условии полноты пространства Y, это линейное многообразие замкнуто, т.е. является подпространством.

Теорема 2. Если последовательность вполне непрерывных операторов {An}, отображающих нормированное пространство X в банахово пространство Y, равномерно сходится к оператору А , т.е. 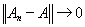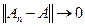, то А также будет вполне непрерывным оператором.

Доказательство. Необходимо доказать, что А отображает всякое ограниченное множество пространства X в относительно компактное множество пространства Y.

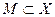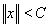
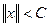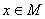
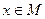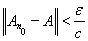
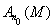
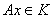
Пусть ограниченное множество в X, тогда для любого и некоторой константы С. Для заданного ε > 0 найдем номер n0 такой, что . Тогда множество = N есть ε – сеть для A(M)=K. В самом деле, для любого имеем .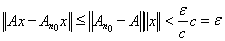

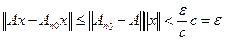Так как, в силу вполне непрерывности 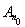и ограниченности M множество N относительно компактно, то мы получаем, что K при любом ε>0 имеет компактную ε -сеть и потому само относительно компактно. Итак, оператор А отображает произвольное ограниченное множество в относительно компактное, и, следовательно, вполне непрерывен. Теорема доказана.

Таким образом, совокупность всех вполне непрерывных операторов из нормированного пространства Х в банахово пространство Y является подпространством L(X, Y). Мы будем обозначать это подпространство K(X, Y).

Пример 2. В пространстве L2[a,b] рассмотрим интегральный оператор

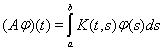
с ядром, имеющим интегрируемый квадрат:

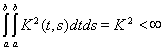
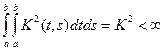(1)

Покажем, что оператор А вполне непрерывен.

Ранее мы показали, что этот интегральный оператор является ограниченным оператором в гильбертовом пространстве H = L2[a,b]. Если функция K(t, s) имеет вид

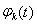
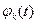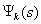
где , , 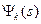k=1,…,n – функции с интегрируемым квадратом (такое ядро K(t,s) называется вырожденным), то оператор А ограничен и

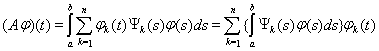
т.е. оператор А переводит все пространство L2[a,b] в конечномерное пространство, порожденное функциями 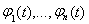. А поскольку всякое ограниченное множество в конечномерном пространстве компактно, то это означает, что интегральный оператор с вырожденным ядром является вполне непрерывным.

Пусть теперь K(t, s) – произвольная функция, квадратично интегрируемая в области 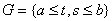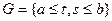. Тогда эту функцию можно разложить (по метрике L2(G) в ряд вида (двойной ряд Фурье))

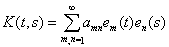
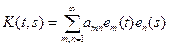(2)

В качестве функций en(t) можно взять любую полную ортогональную систему в пространстве L2[a,b]. В этом случае произведения em(t)en(s) (m, n = 1, 2,…) образуют полную ортогональную систему в пространстве L2(G).

Вырожденные ядра, построенные по частным суммам Kpq(t,s) ряда (2)

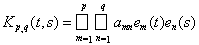
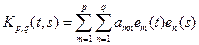
образуют последовательность вполне непрерывных операторов.

.

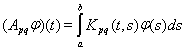
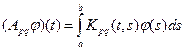Используя оценку нормы оператора (см. выше), получим неравенство

,

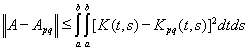
из которого следует, что операторы Apq при 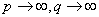сходятся по норме к оператору А. Применяя теорему 2, заключаем, что вместе с операторами Apq, оператор А также вполне непрерывен, что и утверждалось.

Исследование, описанное в статье про 1. Вполне непрерывные операторы и их свойства. Операторы Фредгольма и Гильберта-Шмидта, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 1. Вполне непрерывные операторы и их свойства. Операторы Фредгольма и Гильберта-Шмидта и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ