Лекция
Привет, Вы узнаете о том , что такое 4. Ортогональность и ортогональное дополнение, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 4. Ортогональность и ортогональное дополнение , настоятельно рекомендую прочитать все из категории Функциональный анализ.
Элемент х называется ортогональным подпространству 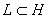
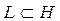 , если х ортогонален любому элементу
, если х ортогонален любому элементу 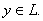
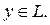 В этом случае записывают
В этом случае записывают 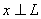
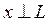 .
.
Имеет место следующая весьма важная теорема.
Теорема 9. Если 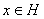
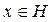 и L – некоторое подпространство гильбертова пространства H, то
и L – некоторое подпространство гильбертова пространства H, то
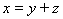
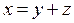 (4),
(4),
где 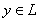
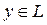 и
и 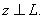
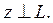 Указанное разложение единственно.
Указанное разложение единственно.
Доказательство. Если 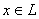
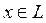 , то, очевидно
, то, очевидно 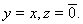
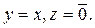 Предположим поэтому, что
Предположим поэтому, что 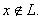
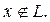 Пусть
Пусть 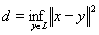
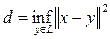 и {yn} – последовательность из L такая, что
и {yn} – последовательность из L такая, что 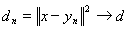
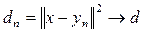 при
при 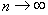
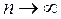 .
.
Пусть далее, h – любой элемент из L, отличный от нулевого вектора. Тогда yn+ εh 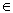
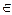 L для любого ε, и поэтому
L для любого ε, и поэтому 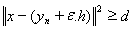
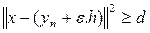 , т.е.
, т.е. 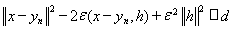
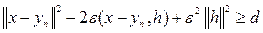 .
.
Полагая
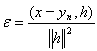
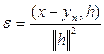
получаем, что 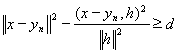
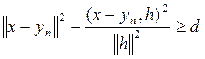 , откуда
, откуда 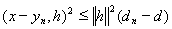
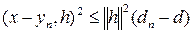 или
или
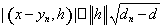
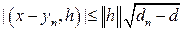 (5).
(5).
При h = 0, неравенство (5) также очевидно выполняется. Об этом говорит сайт https://intellect.icu . Из этого неравенства для любого 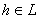
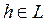 следует
следует
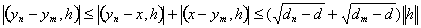
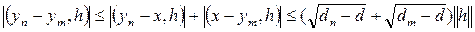 ,
,
и полагая, в частности, 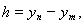
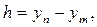 получим
получим 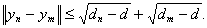
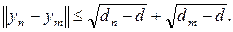
Поэтому последовательность {yn} фундаментальна, а значит, в силу полноты H, сходится к некоторому вектору 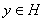
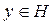 . Так как L замкнуто, то
. Так как L замкнуто, то 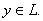
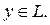
Переходя к пределу в неравенстве (5), получаем, что 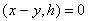
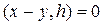 , и так как h – любой элемент из подпространства L, то
, и так как h – любой элемент из подпространства L, то 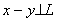
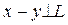 . Полагая
. Полагая 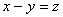
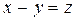 , получаем требуемое равенство
, получаем требуемое равенство 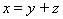
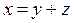 .
.
Докажем теперь единственность этого представления. Пусть 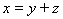
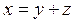 ,
, 
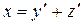 , где
, где 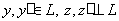
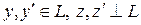 . Тогда
. Тогда 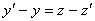
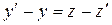 и
и
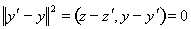
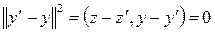 , (6)
, (6)
ибо 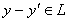
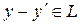 , а
, а 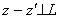
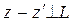 . Но (6) означает, что
. Но (6) означает, что 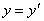
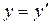 . Следовательно, также
. Следовательно, также 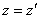
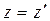 . Теорема доказана.
. Теорема доказана.
Элемент y в разложении (4) называется проекцией вектора x на подпространство L. Из предыдущего видно, что совокупность M всех векторов, ортогональных подпространству L есть также подпространство, которое называется ортогональным дополнением к подпространству L и обозначается H - L; говорят также, что H есть ортогональная сумма подпространств L и M, и пишут H = LÅM. Можно, также, сказать, что элемент z 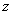
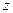 предыдущего разложения есть проекция элемента x на подпространство M.
предыдущего разложения есть проекция элемента x на подпространство M.
Теорема дает, таким образом, разложение на два взаимно дополнительных ортогональных подпространства.
Теорема 9. Для того чтобы линейное многообразие М было всюду плотно в Н, необходимо и достаточно, чтобы не существовало вектора, отличного от нулевого и ортогонального всем элементам многообразия М.
Необходимость. Прежде всего очевидно, что из 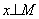
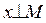 следует
следует 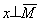
 . Но по условию
. Но по условию 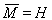
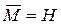 и, следовательно,
и, следовательно, 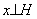
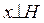 , в частности
, в частности 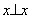
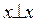 , откуда следует, что
, откуда следует, что 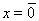
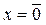 , и необходимость доказана.
, и необходимость доказана.
Достаточность. Пусть М не всюду плотно в Н. Тогда 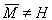
 и существует элемент
и существует элемент 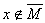
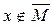 . По предыдущей теореме имеем
. По предыдущей теореме имеем 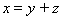
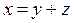 , где
, где 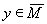
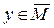 ,
, 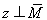
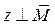 , и так как
, и так как 
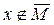 , то
, то 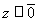
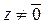 ; что противоречит условию, и достаточность доказана.
; что противоречит условию, и достаточность доказана.
Исследование, описанное в статье про 4. Ортогональность и ортогональное дополнение, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 4. Ортогональность и ортогональное дополнение и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ
Из статьи мы узнали кратко, но содержательно про
Комментарии
Оставить комментарий
Функциональный анализ
Термины: Функциональный анализ