3. Определение интеграла Лебега в произвольном случае кратко

Привет, Вы узнаете о том , что такое 3. Определение интеграла Лебега в произвольном случае, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 3. Определение интеграла Лебега в произвольном случае , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Пусть задано пространство с счетно-аддитивной мерой (Х, S, m), которая уже не обязана быть конечной. Так же как и выше для произвольного множества Е и неотрицательной измеримой функции f (x) (которая может быть уже неограниченной) по разбиению строим верхние и нижние суммы Дарбу. В данном случае уже нельзя утверждать, что суммы являются ограниченными. Однако эти суммы остаются ограниченными снизу, так как функция f является ограниченной снизу.

Определение 2. Интегралом Лебега от измеримой и неотрицательной функции f (x) на множестве Е ÎS называется точная верхняя грань ее нижних сумм Дарбу

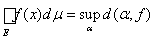
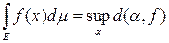
Неотрицательная измеримая функция f (x) называется интегрируемой по Лебегу на Е, если этот интеграл конечен.

Отметим, что данное определение для ограниченных функций не дает ничего нового (см. теорему 1).

Заметим также, что определение интеграла Лебега распространяется на функции, которые могут принимать и бесконечные значения. Необходимо только, чтобы множество точек, в которых функция f (x) обращается в бесконечность имела нулевую меру (такую функцию называют конечной почти всюду).

Пусть h – некоторая простая функция, принимающая зна­чения y1, y2, … , yn, yi ¹ yj при i j, и пусть E – некоторое измеримое подмножество X.

Лемма 3. Интеграл от простой неотрицательной измеримой функции h(x) вычисляется по формуле

= ,

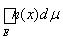
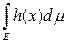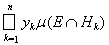
где функция 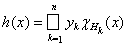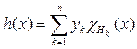принимает значения yk ³ 0 на множестве Hk ÎS.

Доказательство. Пусть задано произвольное разбиение a = 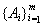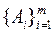множества Е. Обозначим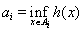 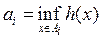. Так как имеет место неравенство ai £ yj для любого х Î Bij = AiÇHj (если последнее множество не пусто), то из аддитивности меры следует

.

Если разбиение a в точности совпадет с системой {Hk}, то в этом неравенстве должен быть знак равенства. Лемма доказана.

Отметим, что для интегрируемости простой функции необходимо, чтобы мера множеств Hk, на которых она принимает не нулевые значения должна быть конечной. Установим некоторые свойства интеграла Лебега от простых функций

A) = + .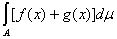

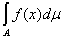
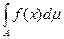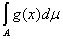
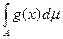Для доказательства предположим, что f принимает значения fi на множествах Fi Ì A, a g – значения gj на множествах Gj Ì A, так что

J1= = ,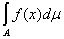

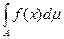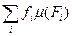J2= = .

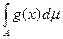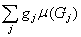
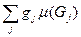Тогда в силу леммы 3

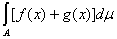
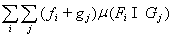
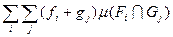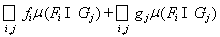
J = = = = 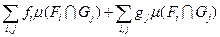J1 + J2.

Б) Для любого постоянного k справедливо равенство 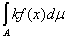=k 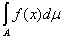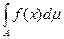(проверяется непосред­ственно.)

Лемма 3 позволяет на самом деле подойти к определению интеграла Лебега от неотрицательных измеримых функций еще с одной стороны.

Теорема 9. Об этом говорит сайт https://intellect.icu . Интеграл Лебега от неотрицательной измеримой функции f (x) на множестве Е равен верхней грани интегралов от простых неотрицательных измеримых функций h(x) и таких, что h(x) £ f (x) при всех х Î Е, т.е.

.

Доказательство. Если h(x) £ f (x) при всех х Î Е, то из определения интеграла сразу следует, что .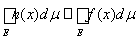

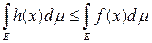С другой стороны, в силу леммы 3 каждая нижняя сумма Дарбу является интегралом от некоторой простой функции h(x) £ f (x). Отсюда верхняя грань интегралов простых функций совпадает с интегралом от f (x).

Полученная теорема позволяет подойти еще с одной стороны к определению интеграла.

Теорема 10. Интеграл Лебега от неотрицательной измеримой функции f (x) на множестве Е равен верхней грани интегралов от ограниченных неотрицательных измеримых функций h(x) таких, что h(x) £ f (x) при всех х Î Е, т.е.

.

Доказательство. Так как любая простая функция является одновременно ограниченной, имеем по теореме 9

,

где супремум взят по всем ограниченным неотрицательным измеримым функциям h(x) таким, что h(x) £ f (x) при всех х Î Е. Если функция р(х) является простой, неотрицательной, измеримой и удовлетворяющей неравенству р(х) £ h(x), то тем более р(х) £ f (x). Последнее по теореме 9 означает, что

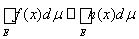
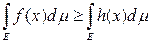
для любой ограниченной неотрицательной измеримой функции h(x) такой, что h(x) £ f (x) при всех х Î Е. Это неравенство вместе с предыдущим доказывает теорему.

Полученная теорема позволяет получить значение интеграла еще одним способом, который позволяет легко перенести все основные свойства интеграла на произвольную неотрицательную функцию.

Пусть f (x) произвольная неотрицательная измеримая функция. Введем понятие срезки этой функции

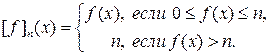
Ясно, что срезка является ограниченной измеримой функцией. При этом для любой ограниченной неотрицательной измеримой функции h(x) такой, что h(x) £ f (x) найдется номер N такой, что выполняется неравенство h(x) £ [f ]n (x) для n ³ N. Последнее означает, что для n ³ N справедливы неравенства

.

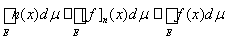
При этом внутренние интегралы возрастают с ростом n. Эта система неравенств и теорема 10 позволяют сформулировать следующий результат.

Теорема 11. Интеграл Лебега от неотрицательной измеримой функции f (x) на множестве Е равен пределу интегралов от срезок функций f (x), т.е.

.

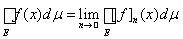
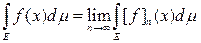Дадим теперь определение интеграла Лебега от произвольной измеримой функции. Для этого введем понятие положительной и отрицательной составляющих функций:

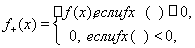
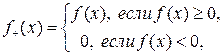
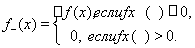
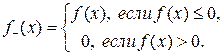
Введенные функции являются измеримыми. Достаточно очевидны представления f (x) = f +(x) + f –(x), |f (x)| = f +(x) – f –(x).

Определение 3. Интегралом Лебега от измеримой функции f (x) на множестве Е ÎS называется

.

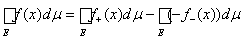
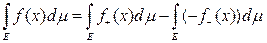При условии, что каждый интеграл, стоящий справа конечен, функция f (x) называется интегрируемой по Лебегу на Е и пишут f (x) Î L(E).

Данное определение сразу показывает, что если функция f (x) интегрируема, то интегрируемой является также функция | f (x)|.

Полученные в предыдущем пункте свойства интеграла от ограниченной функции, теорема 11 и определение 3 позволяют легко переформулировать свойства и в общем случае.

Теорема 12. 1) (полная или счетная аддитивность интеграла по области интегрирования). Пусть на измеримом множестве Е задана изме­римая функция f(x). Если множество Е есть сумма конечного числа или счетного множества попарно не пересекаю­щихся измеримых множеств E = 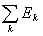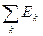(EkÇEi = Æ, k ¹ i ), то

=

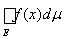
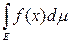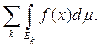
2) Если интеграл от неотрицательной из­меримой функции f(x) равен нулю, то эта функция эквивалентна нулю.

3) (свойство аддитивности интеграла). Если на измеримом множестве E заданы две интегрируемы по Лебегу функции f(x) и g(x), то

= + .

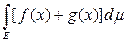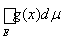
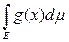4) (свойство однородности интеграла). Если на измеримом множестве Е задана интегрируемая по Лебегу функция f(x) и с есть конечная постоянная, то

= c .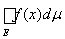

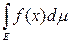5) (свойство монотонности интеграла) Пусть f(x) и F(х) интегрируемы на измеримом множестве Е. Если f(x) £ F(x), то

£ .

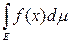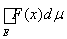
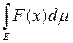6) Если функция f(x)интегрируемая на измеримом множестве E, то

£

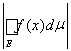
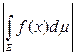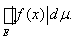
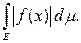
Исследование, описанное в статье про 3. Определение интеграла Лебега в произвольном случае, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 3. Определение интеграла Лебега в произвольном случае и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ

Из статьи мы узнали кратко, но содержательно про