1. Системы множеств кратко

Привет, Вы узнаете о том , что такое 1. Системы множеств, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 1. Системы множеств , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Определение 1. Пусть М - произвольное множество. Непустая система K неко­торых его подмножеств называется кольцом, если для " А, В Î K

1. AÈB Î K.

2. A\B Î K.

Из этого определения следуют ряд простых следствий. В частности, любое кольцо K содержит пустое множество (Æ = А\А); вместе с множествами А и В кольцо K содержит и симметрическую разность АDВ = (А\В)È(В\А); кольцо также замкнуто относительно операции пересечения АÇВ = (АÈВ)\(АDВ).

Замечание. В учебниках можно встретить разные определения кольца множеств. Эти определения эквивалентны между собой.

Определение 2. Непустая система A подмножеств множества М называется ал­геброй, если

1. Если А, В Î A, то A È В Î A.

2. Если АÎ A, то АС = М\А Î A.

Теорема 1. Для того чтобы система K подмножеств множества М была алге­брой, необходимо и достаточно, чтобы она была кольцом и М Î K.

Необходимость. Пусть система множеств K является алгеброй и А, В Î K. Тогда по второму АС, ВСÎK. Об этом говорит сайт https://intellect.icu . Следовательно (1 свойство) АС È ВС ÎK и снова по второму свойству (АС È ВС)С = АÇВ ÎK. Следовательно алгебра замкнута относительно операции пересечения.

Используя представление А\В = (АÇВС) получаем, что алгебра замкнута также и относительно операции вычитания множеств. Последнее доказывает, что она является кольцом.

Так как пустое множество принадлежит кольцу K, то и ÆС = М также принадлежит K.

Достаточность. Пусть кольцо K содержит множество М. Тогда, по свойствам кольца, будут выполнены первое и второе свойство алгебры.

Определение 3. Непустая система S подмножеств множества М называется s-кольцом, если оно кольцо, замкнутое по отношению к объединению не только конечного, но и счетного множества множеств, т.е. если

1.из Ai Î S, (i = 1, 2,...) следует, что А = 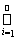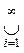Ai Î S

2.из А, В Î S следует, что А\В Î S.

Требование, чтобы объединение конечного числа множеств из S входило в S, здесь уже содержится, т.к. в условии 1, в частности, можно взять все Ai, начиная с некоторого, равными пустому множеству.

Определение 4. Непустая система A подмножеств множества М называется s-алгеброй, если она удовлетворяет условию (1) из определения s-кольца и условию (2) из определения алгебры.

Следующая теорема доказывается аналогично теореме 1.

Теорема 2. Для того чтобы совокупность S была s-алгеброй, необходимо и достаточно, чтобы она была s-кольцом и чтобы М Î S.

Определение 5. Пусть К – произвольная непустая совокупность подмножеств множе­ства М, тогда всегда существует наименьшее кольцо (алгебра, s-кольцо или s-алгебра), содержащее К Ì K.

Действительно, таким K будет пересечение всех колец K' (алгебр, s-колец или s-алгебр), состоящих из подмножеств множества М и содержащих К (та­кие K' существуют, например, совокупность всех подмножеств множества М), эта совокупность K называется кольцом (алгеброй, s-кольцом или s-алгеброй), порожденным совокупностью К.

Определение 6. Система P подмножеств множества М называется полуколь­цом, если она удовлетворяет следующим условиям:

1. Æ Î P;

2. если А, В Î P, то АÇВ Î P;

3. если A, B ÎP и B Ì A, то существует конечная совокупность таких дизъюнктных множеств Сn Î P, что А \ В = 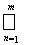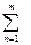Cn.

Из указанных свойств кольца вытекает, что любое кольцо является полукольцом.

Исследование, описанное в статье про 1. Системы множеств, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 1. Системы множеств и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ

Из статьи мы узнали кратко, но содержательно про