1. Линейные непрерывные функционалы. Продолжение по непрерывности. Теорема Хана-Банаха. Следствия из теоремы Хана-Банаха кратко

Привет, Вы узнаете о том , что такое 1. Линейные непрерывные функционалы. Продолжение по непрерывности. Теорема Хана-Банаха. Следствия из теоремы Хана-Банаха, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 1. Линейные непрерывные функционалы. Продолжение по непрерывности. Теорема Хана-Банаха. Следствия из теоремы Хана-Банаха , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Частным случаем линейного оператора является линейный функционал. Если областью определения линейного непрерывного оператора является произвольное линейное нормированное пространство X, а значениями его являются вещественные числа R (или комплексные числа C, если пространство определено над полем комплексных чисел), то такой линейный оператор называется линейным непрерывным функционалом f(x), определенным на пространстве Χ.

Так как числовая прямая есть частный случай банахова пространства, то все, что было сказано выше для линейных операторов, верно и для линейных функционалов. Например, норма линейного функционала f(x) есть число

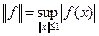
и для любого 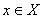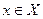выполняется неравенство

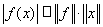
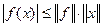
Нетрудно видеть также, что

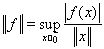
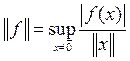
Верны также все теоремы, доказанные выше для линейных непрерывных операторов.

В частности, для того, чтобы линейный функционал, определенный на линейном нормированном пространстве Х, был непрерывен, необходимо и достаточно, чтобы он был ограничен.

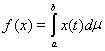
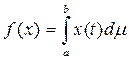Пример 1. Пусть X = L2[a, b] и . Рассматривая этот интеграл как скалярное произведение функции 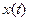на функцию, тождественно равную единице,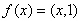 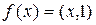, получаем в силу неравенства Буняковского, что |f (x)| = |(x, 1)| £ ||x||×||1|| =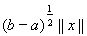 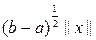, ограничен. Аддитивность и однородность очевидны. Следовательно, 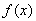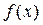– линейный непрерывный функционал. Нетрудно видеть, что .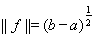

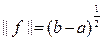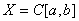
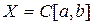Пример 2. Пусть . Положим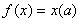 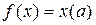. Аддитивность и однородность этого функционала очевидны. Так как, далее, |f (x)| = |x(a)| £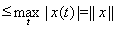 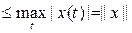, то 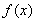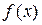– ограниченный и, следовательно, непрерывный функционал. Снова легко проверить, что .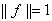

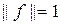Пример 3. Пусть Х = Rn, то есть k-мерное евклидово пространство. Для элемента 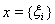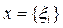этого пространства положим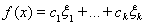 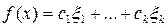, где 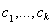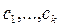– некоторые константы. Аддитивность и однородность функционала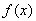 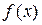снова очевидна. Так как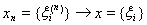 означает, что 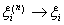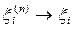для всех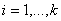 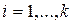, то

,

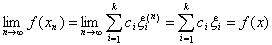
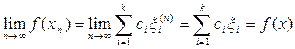и непрерывность 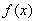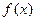доказана.

Замечание. Норме линейного функционала можно дать геометрическое истолкование. Так как в 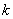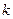- мерном евклидовом пространстве уравнение плоскости

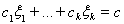
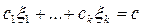
можно записать в виде 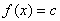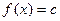, то по аналогии назовем гиперплоскостью в произвольном линейном пространстве X совокупность точек этого пространства, удовлетворяющих уравнению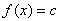 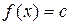, где f есть линейный непрерывный функционал на X. Об этом говорит сайт https://intellect.icu . Гиперплоскост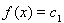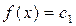и и 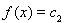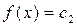естественно назвать параллельными.

Гиперплоскость 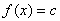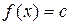делит пространство X на два полупространства: совокуп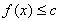ность точек x, в которых , и совокупность точек x, в которых 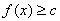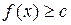. Гиперплоскость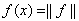 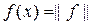обладает тем свойством, что весь единичный шар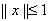 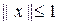лежит целиком по одну сторону от этой гиперплоскости (ибо для точек шара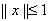 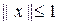мы имеем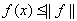 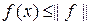). С другой стороны, никакая из параллельных гиперплоскостей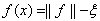 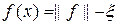этим свойством уже не обладает. Так, что естественно гиперплоскость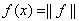 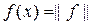назвать опорной (или касательной) к шару .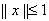

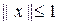Рассмотрим принцип продолжения по непрерывности для ограниченного оператора А: L ® F, заданного на некотором всюду плотном подпространстве L Ì E нор­мированного пространства Е.

Теорема 1(продолжение по непрерывности). Пусть L Ì Е всюду плотное подпространство в Е u F есть банахово пространство. Тогда для каждого ограничен­ного оператора A: L ® F существует единственный ограниченный оператор B:E ® F такой, что Вх = Ах при всех xÎL и ||B|| = ||А||.

Доказательство. По условию плотности подпростран­ства L в Е для каждого х Î Е найдется такая после­довательность {хn} Ì L, что 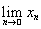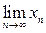= x. Так как ||Axi – Axj|| = ||A(xi – xj)|| £ ||A||×|| xi – xj||, то последовательность векторов {Ахn} фундаментальна в пространстве F. В силу полноты F существует предел Вх =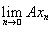 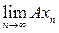. Возьмем еще один вектор у Î Е и выберем последовательность векторов {yk} Ì L, сходящуюся к у. Поскольку предел суммы равен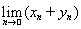 = x+y, то из линейности оператора А вытекают равенства:

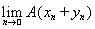
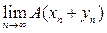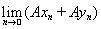
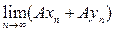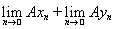
В(х + у) = = = = 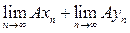Вх + By.

В частности, полагая здесь у = – х, получим, что значение оператора Вх не зависит от выбора последовательности, сходящейся к элементу х. Аналогично проверяется, что В(lх) = lВх. Таким образом, оператор В линейный. Так как Вх = Ах при всех x Î L, то ||В|| ³ ||A||. С другой стороны, в силу непрерывности нормы ||Bx|| = 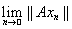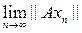£ ||A||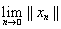 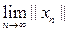£ ||A||×||x|| при всех хÎЕ. Следовательно, ||В|| £ ||A|| и значит спра­ведливо равенство ||B|| = ||А||. Единственность оператора продолжения В следует из его определения.

Пример 4. Рассмотрим пространство С[0, 1] непрерывных функций на отрезке [0, 1] с чебышевской нормой и его ли­нейное подпространство Ã всех алгебраических полиномов P(х) = 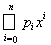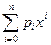. По теореме Вейерштрасса подпространство Ã всюду плотно в пространстве С[0,1].

Пусть в подпространстве Ã действует оператор дифферен­цирования DP(x) = Р¢(х), где РÎÃ. Так как ||Dxi|| = i при всех натуральных i, то оператор неограничен и ||D|| = ¥. Ясно, что опера­тор дифференцирования нельзя продолжить на пространство С[0,1] так, чтобы он был ограниченным оператором.

Если сузить оператор Р на подпространство Ãn полино­мов степени не выше n, то получится ограниченный оператор Dn, который уже имеет ограниченное продолжение в C[0, l]. Для доказательства достаточно взять ограниченный оператор Bnf(x) = Ln¢(х), где Ln(х) есть интерполяционный многочлен Лагранжа степени n для функции f(x) Î С[0, 1].

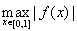
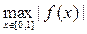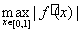
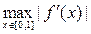Оператор дифференцирования Df(x)=f(x) можно рассмат­ривать на пространстве С1[0, 1] непрерывно дифференцируе­мых функций на отрезке [0, 1] с нормой ||f ||1 = + и со значениями в пространстве С[0, 1]. Тогда получится огра­ниченный оператор, который является продолжением операто­ра D, заданного на подпространстве Ã.

Рассмотрим линейный функционал f: L ® R, задан­ный на подпространстве L Ì Е. Линейный функционал g: Е ® R называется продолжением функционала f на пространство Е, если g(х) = f (x) при всех х Î L.

Следующая теорема занимает центральное место в функциональном анализе.

Теорема 2 (Хана-Банаха). Пусть в пространстве Е задана полунорма р(х), т.е. вещественная функция на Е, удовлетворяющая условиям: 1) р(lх) = lр(х) для любого l³ 0 и любого хÎЕ; 2) р(x + y) £ p(x) + p(y), "x, y ÎE..

Пусть L подпространство E. Тогда каждый линейный функционал f: L ® R, удовлетворяющий условию |f(х)| £ р(х) при всех xÎ L, имеет такое продолжение g: E ® R на все простран­ство Е, что |g(x)| £ p(x) при всех хÎ Е.

Доказательство. Пусть вектор e1Ï L и подпро­странство L1 = span{L,e1} является линейной оболочкой подпространства L и вектора е1. Так как для всех x, yÎL имеют место неравенства

f(х) + f(у) = f(х + у) £ p(x + y) £ p(x – e1) + p(y + e1),

то f(x)– p(x — el) £ p(y + e1) – f(y). Поэтому по аксиоме Дедекинда найдется такое число c1Î R, что

f(x)– p(x — el) £ c1 £ p(y + e1) – f(y)

при всех х, у ÎL. Подставляя сюда х/l вместо х и у, а затем умножая на l, имеем f(x) ± lc1 £ р(х ± lе1) при всех l > 0 и при всех х ÎL.

Определим функционал f1, на подпространстве L1 по формуле f1(z) = f(x) + lc1 для всех z= х+lе1 Î L1, где х Î L и lÎR. Тогда f1(x) = f(x) для всех xÎL и по доказанному выше f1(z) £ p(z) для всех z ÎL1. Так как полунорма обладает свойством симметрии p(–z) = p(z), то справедливо неравенство |f1(z)| £ p(z).

Аналогично можно доказать существование продолже­ния f2 на линейную оболочку L2 = span{L1, e2}, где век­тор е2 ÏL1, и т. д. Поэтому, если пространство Е имеет конечную или счетную размерность, то доказательство теоремы завершается по индукции.

В общем случае рассмотрим совокупность À всех g продолжений функционала f на некоторые подпростран­ства G Ì E, удовлетворяющие условию |g(x)| £ p(x) при всех х Î G. Введя отношение порядка g1 £ g2, если g2 является продолжением g1, получим частично упорядо­ченное множество линейных функционалов.

По лемме Цорна в множестве À существует макси­мальный элемент g. Как показано выше, каждый линей­ный функционал можно продолжить на более широкое подпространство. Поэтому максимальный функционал g должен быть определенным на всем пространстве G = E и значит удовлетворяет теореме.

Пусть функционал f : L ® R определен на подпространстве LÌE нормированного пространства Е. Тогда норма этого функционала вычисляется по формуле:

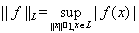
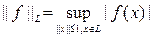
Одним из следствий теоремы Хана-Банаха является воз­можность продолжения функционала f на все простран­ство Е с сохранением его нормы на подпространстве L. Однако, как показывают примеры, такое продолжение не всегда обладает свойством единственности.

Следствие 1. Для каждого линейного ограниченного функциона­ла f :L ® R, заданного на подпространстве L банахова пространства E, суще­ствует такое его продолжение g: E ® R на все простран­ство Е, что ||g|| = ||f ||L.

Доказательство. Применяя теорему Хана-Банаха, где в качестве полунормы взята функция р(х) = ||f ||L||x||, мы получим неравенство |g(x)| £ ||f ||L||x|| при всех хÎЕ.

Отсюда следует ||g || £ ||f ||L. Поскольку функционалы совпадают g(x) = f (х) всех x Î L, то ||g|| = || f ||L.

Следствие 2. Для любого элемента х ¹ 0 банахова пространства Е существует линейный функционал f ÎE* такой, что 1) ||f || = 1; 2) f(x) = ||x||.

Доказательство. Рассмотрим одномерное пространство L, порожденной вектором х. Определим линейный непрерывный функционал на L по правилу f (lx) = l||x||. Этот функционал на L удовлетворяет условиям 1 и 2 следствия. Действительно, f(x) = ||x||, 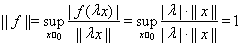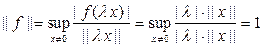. Осталось продолжить этот функционал на все Е с сохранением нормы.

Следствие 3. Для любого элемента х ¹ 0 банахова пространства Е справедливо равенство ||x|| = .

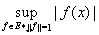
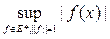Доказательство легко вытекает из следствия 2 и неравенства |f (x)| £ ||f ||×||x||.

Следствие 4. Если для элемента х банахова пространства Е для любого линейного непрерывного функционала f выполняется равенство f(x) = 0, то х = 0.

Это сразу вытекает из следствия 3.

Исследование, описанное в статье про 1. Линейные непрерывные функционалы. Продолжение по непрерывности. Теорема Хана-Банаха. Следствия из теоремы Хана-Банаха, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 1. Линейные непрерывные функционалы. Продолжение по непрерывности. Теорема Хана-Банаха. Следствия из теоремы Хана-Банаха и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ