3. Критерий полноты пространства кратко

Привет, Вы узнаете о том , что такое 3. Критерий полноты пространства, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 3. Критерий полноты пространства , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Определение 7. Пусть дано метрическое пространство (X, d) и последовательность замкнутых шаров S[xk, rk]. Такая система шаров называется вложенной, если:

1. S[x1, r1] É S[x2, r2] É...;

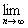
2. 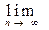rn = 0.

Теорема 2. X - метрическое пространство является полным тогда и только тогда, когда любая вложенная система шаров в Х имеет не пустое пересечение (существует единственная точка принадлежащая каждому шару системы).

Необходимость. По 2) условию для вложенной системы для " e > 0 $ N: 0 < rk < e, если k ³ N. Рассмотрим последовательность центров этих шаров. В силу условия 1) xk Î S[xN, rN], если k ³ N, то есть d(xN, xk) £ rN < e. Тогда по неравенству треугольника легко получаем, что d(xn, xk) < 2e для всех n, k ³ N. Таким образом, {xk} - фундаментальная последовательность в пространстве Х. В силу полноты этого пространства существует х = 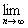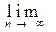хn. По 1) условию xn Î S[xk, rk] при n ³ k и xn ® x. В силу замкнутости шара S[xk, rk] это означает, что x Î S[xk, rk] и это верно для произвольного k. Отсюда x принадлежит пересечению этих шаров.

Используя свойство 2) вложенной системы шаров и неравенство треугольника для метрики покажите самостоятельно единственность этой точки.

Достаточность. Возьмем yk Î X - произвольную фундаментальную последовательность в пространстве Х. Тогда для "ek = (1/2)k $nk: d( 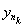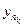, ym) < (1/2)k при m ³ nk. Об этом говорит сайт https://intellect.icu . По последовательности {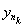 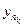} построим следующую систему вложенных шаров 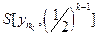. Для проверки вложенности этой системы очевидно достаточно проверить лишь первое условие в определении. Пусть уÎ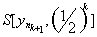 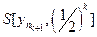. 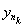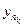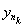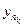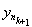Тогда d( , y) £ d( , ) + d( 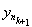, y) £ (1/2)k + (1/2)k £ (1/2)k-1, т.е. 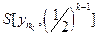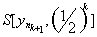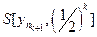уÎ и Ì .

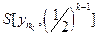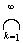
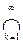
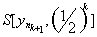
Следовательно 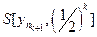= {x0}. Тогда 0 £ d(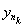 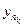, x0) £ (1/2)k-1, то есть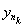 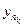® x0 (k ® ¥). Тогда в силу леммы 4 сама последовательность {yk} сходится к х0.

Теорема доказана.

Определение 8. Диаметром множества М метрического пространства (Х, d) называется число diamM = sup d(x, y), где супремум берется по всем х, у ÎМ.

Определение 9. Система замкнутых множеств Мn метрического пространства (X, d) называется вложенной, если выполнены следующие два условия:

1) М1 É М2 É М3 É ... É Мn É...;

2) diam Mn ® 0 при n ® ¥.

Следующая теорема является аналогом теоремы 2 и доказывается точно таким же образом.

Теорема 3. X - метрическое пространство является полным тогда и только тогда, когда любая вложенная система замкнутых множеств Мn в Х имеет не пустое пересечение (существует единственная точка принадлежащая каждому множеству системы).

Следующий пример показывает важность условия стремления к нулю диаметра множеств в определении вложенной системы.

Пример 9. В пространстве l2 положим Mn = {x = (0, ..., 0, xn, xn+1, ...)}Îl2: 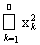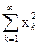= 1}. Нетрудно видеть, что эти множества замкнуты, удовлетворяют условию 1) и не удовлетворяют условию 2) (вычислите диаметры рассмотренных множеств) определения 9. Достаточно очевидно, что их пересечение является пустым множеством.

Исследование, описанное в статье про 3. Критерий полноты пространства, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 3. Критерий полноты пространства и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ