1. Понятие множества. Операции над множествами. Отображения. Характеристическая функция множества кратко

Привет, Вы узнаете о том , что такое 1. Понятие множества. Операции над множествами. Отображения. Характеристическая функция множества, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 1. Понятие множества. Операции над множествами. Отображения. Характеристическая функция множества , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Понятие множества изучалось студентами в курсе математического анализа. Здесь мы напомним основные понятия и термины из этой теории.

Понятие множества является настолько общим, что затруднительно дать для него формальное определение (т.е. сведение его к другим понятиям, более простым и более ясным).

Мы будем рассматривать множества чисел, множества точек, множество линий, множества функций и т.д. Множества будем обозначать большими буквами: A, B, M, N и т.д. Объекты, из которых состоит множество, называются элементами множества, будем обозначать их малыми буквами. Запись 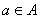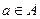(или ) означает, что a есть элемент множества A; запись означает, что a не является элементом множества A. Запись 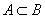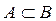(или 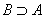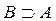) означает, что каждый элемент множества A является элементом множества B; в этом случае множество A называют подмножеством множества B. Если имеют место включения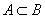 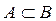, В Ì А, то это означает, что множества A и B состоят из одних и тех же элементов и, значит, совпадают друг с другом. Этот факт записывается равенством A = B. Существует одно специальное множество, так называемое пустое множество, которое не содержит ни одного элемента. Пустое множество обозначается символом Æ.

Рассмотрим простейшие операции, которые можно производить над множествами: объединение, пересечение и дополнение.

Пусть дано семейство множеств {Aa}a, где индекс a пробегает некоторое множество Т. Рассмотрим совокупность всех элементов, каждый из которых принадлежит хотя бы одному из множеств Aa. Эта совокупность есть новое множество, которое и называют объединением множеств Aa и обозначается 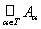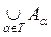.Отметим, что если какой либо элемент входит в несколько множеств, то в объединение этих множеств он включается только один раз. В соответствии с аксиомами теории множеств пустое множество является подмножеством любого множества.

Пусть снова дана совокупность множеств {Aa}aÎТ. Множество, состоящее из тех и только тех элементов, которые принадлежат каждому из указанных множеств, называется пересечением множеств и обозначается .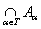

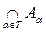В случае, если для a ¹ b, a, bÎ Т выполняется равенство АaÇАb = Æ, то объединение 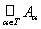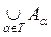называется дизъюнктным и обозначается .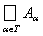

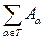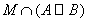
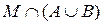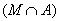
Из определения объединения и пересечения множеств видно, что эти операции обладают свойством коммутативности и ассоциативности. Об этом говорит сайт https://intellect.icu . Легко показать также, что имеет место следующий закон дистрибутивности = 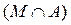È .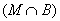

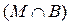Пусть даны множества A и B. Элементы множества A, не принадлежащие B, образуют множество, называемое разностью множеств A и B и обозначаемое A - B или A\B. Нетрудно видеть, что A\B=A\ .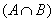

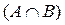Введем еще одно понятие. Если B есть подмножество A, то разность A\B называют дополнением множества B до множества A. Отметим очевидную формулу: если 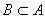, то 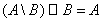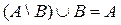. Заметим, что для двух произвольных множеств A и B эта формула вообще неверна.

Из более сложных формул отметим следующие, которые часто будут встречаться.

Теорема (принцип двойственности). Пусть дана система множеств Аα и множество Ω, причем Аα 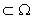. Тогда

Èa(W - Аa) = W - (ÇaАa);

Ça(W - Аa) = W - (ÈaАa).

Отображением φ множества M1 в множество M2 (обозначение φ: M1®M2) называется такой закон φ, при котором каждому элементу xÎM1 поставлен в соответствие один и только один элемент yÎM2, обозначаемый через φ(x) и называемый образом элемента x при отображении φ.

Совокупность всех тех элементов aÎM1, образом которых является данный элемент bÎM2, называется прообразом элемента b при отображении φ:M1®M2 и обозначается через φ-1(b). Таким образом, φ-1(b) = {aÎM1: j(a) = b}.

Пусть A - некоторое подмножество из M1; совокупность {φ(a): aÎA} всех элементов вида φ(a), где aÎA, называется образом A и обозначается φ(A). В свою очередь, для каждого множества B 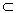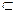M2, определяется его полный прообраз φ-1(B), как совокупность всех тех элементов из M1, образы которых принадлежат B, т.е. φ-1(B) = {aÎM1: j(a) Î В}

Напомним, что отображение φ множества M1 в множество M2 называется сюръекцией, если φ(M1) = M2.

Если для любых двух различных элементов x1 и x2 из M1 их образы y1 = φ(x1) и y2 = φ(x2) также различны, то φ называется инъекцией. Отображение φ: M1 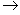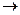M2, которое одновременно является сюръекцией и инъекцией, называется биекцией или взаимно однозначным соответствием между M1 и M2.

Имеют место следующие основные свойства отображений:

Теорема о прообразах. Прообраз объединения или пересечения двух множеств равен объединению или пересечению их прообразов соответственно:

φ-1(A 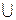B)= φ-1(A) 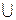φ-1(B),

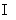
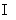
φ-1(A B)= φ-1(A) φ-1(B).

Теорема об образах. Образ объединения двух множеств равен объединению их образов:

φ(A 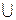B)= φ(A) 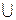φ(B).

Заметим, что образ пересечения двух множеств, вообще говоря, не совпадает с пересечением их образов.

Отображение IM: M®M называется тождественным (или единичным) отображением множества M, если IM(x) = x, " xÎM.

Пусть даны отображения φ: M1® M2 и ψ: M2®M3, тогда можно определить композицию отображений φ и ψ, как отображение ψ 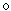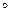φ: M1®M3, определяемое формулой (ψ φ)(x) = ψ(φ(x)) , 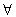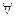xÎM1.

Отображение φ: M1 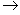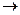M2 называется обратимым, если существует такое отображение ψ:M2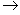 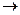M1, что имеют место следующие соотношения:

φ 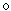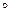ψ = IM2

ψ 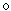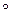φ = IM1

В этом случае отображение ψ называется обратным к отображению φ и обозначается через φ-1 .

Теорема о единственности обратного. Если отображение φ: М1→М2 обратимо, то обратное отображение φ-1 единственно.

Имеет место следующий критерий обратимости отображения.

Теорема о существовании обратного. Отображение φ: М1→М2 обратимо тогда и только тогда, когда φ – биективно.

В этом случае обратное отображение φ-1: М2→М1 определяется (однозначно) следующим образом: образом элемента у 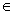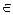М2 при отображении φ -1 будет такой элемент х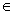 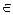М1, который при отображении φ переходит в элемент у. Иными словами: φ-1(у) = х Û φ(х) = у.

Исследование, описанное в статье про 1. Понятие множества. Операции над множествами. Отображения. Характеристическая функция множества, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 1. Понятие множества. Операции над множествами. Отображения. Характеристическая функция множества и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ