2. Сопряженные пространства кратко

Привет, Вы узнаете о том , что такое 2. Сопряженные пространства, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 2. Сопряженные пространства , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Пусть Е — нормированное пространство. Совокупность всех ограниченных функционалов обозначается через Е* и называется сопряженным про­странством к Е. Поскольку линей­ный функционал f : Е ® R можно рассматривать как ли­нейный оператор, действующий из Е в R, то сопряженное пространство Е* совпадает с пространством ограничен­ных операторов L(Е, R). Следовательно, по доказанному ранее, Е* — банахово пространство.

Пример 5. Сопряженное пространство к Rn. Докажем, что сопряженное пространство (Rn)* к евклидовому пространству Rn изометрично самому пространству Rn.

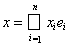
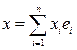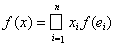
Рассмотрим стандартный базис {еj} пространства Rn, т. е. ej = {eij}, где eij = 0, если i ¹ j, и еii = 1. Для произвольного вектора х = (x1, …, xn) Î Rn и для произвольного функционала f Î (Rn)* имеем равенства: , 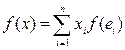. Полагая далее у = (у1, ..., уn), где yi = f (ei), и применяя нера­венство Гельдера, получим неравенство:

.

Если взять вектор х с координатами хi = уi/||у||, то это нера­венство превращается в равенство | f (х)| = ||у||. Следовательно, норма || f || = ||у|| и значит отображение, при котором каждому функционалу f Î (Rn)* соответствует вектор у Î Rn с координа­тами yi = f (ei), является изометричным.

Пример 6. Сопряженное пространство с*. Пространство, обозначаемое через с, состоит из всех сходящихся последова­тельностей х = {хi}, где хi ÎR, i = 1, 2, …, и имеет норму ||x|| = |xi|. Покажем, что каждый функционал f Îс* имеет вид

.

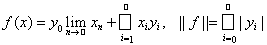
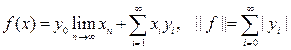Отсюда видно, что сопряженное пространство с* изометрично пространству l1 абсолютно суммируемых последовательностей y = {yi} с нормой ||y|| = .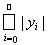

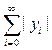Пусть векторы еi из примера 5, а вектор e = {1, 1, ...}. Об этом говорит сайт https://intellect.icu . Обозначая предел через х0 = 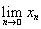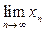для произвольного вектора х = {xi} Î с имеем

.

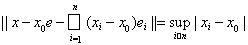
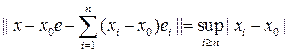Следовательно, ряд 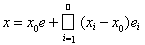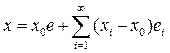сходится по норме пространства с. Далее, используя линейность и непрерывность функционала f Îс*, мы получим

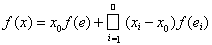
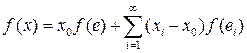
Пусть l = f (е) и yi = f(ei). Если в этой формуле вектор x имеет координаты xi = sgnyi при i £ n и хi, = 0 при i > n, то ||x|| £ 1 и значит при всех n

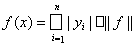
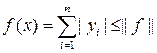
Таким образом, ряд y0 = l – 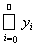сходится абсолютно и фор­мула принимает следующий вид:

.

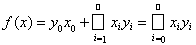
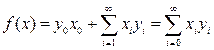Отсюда легко вытекает, что норма || f || £ 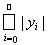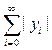Если в указанной формуле положить хi = sgnyi, при i = 1,2,..., n и xi = sgny0 при i > n, то ||x|| = 1 и при всех n будет справедливо неравенство

.

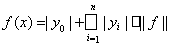
Устремляя n ® ¥, получаем равенство .

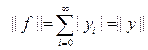Сопряженное пространство Е* является банаховым пространством. Поэтому можно рассматривать второе сопряженное пространство Е** = (Е*)*, состоящее из всех ограниченных функционалов на сопряженном про­странстве Е*. Как и всякое сопряженное пространство оно является банаховым пространством.

Отображение J: Е ® Е** нормированного пространства во второе сопряженное пространство, заданное по фор­муле J(x) = ax, где действие линейного функционала ax Î Е** для всех fÎ Е* определено равенством ax(f ) = f (x), называется отображением двойственности. Далее мы будем обозначать через S* замкнутый единичный шар в Е*.

Введем еще одно полезное понятие. Отображение i: Y ® Х топологических пространств Y, Х называется вложением Y в Х, если: 1) i непрерывно; 2) i: Y ® i(Y) – гомеоморфизм, где i(Y) Ì Х – подпространство в Х, являющееся образом Y при гомеоморфизме i.

Теорема 3 (двойственности). Отображение J явля­ется изометричным вложением пространства Е во второе сопряженное пространство Е**.

Доказательство. По определению отображения J каж­дому вектору х Î Е соответствует функционал ax, опре­деленный на сопряженном пространстве Е* по формуле ax(f ) = f (x) при всех fÎ Е*. Легко проверить, что функ­ционал ax является линейным:

ax (f + g ) = (f + g)(x) = f (x) + g(x) = ax(f ) + ax(g), ax (lf ) = l f (x) = lax(f ).

Для того чтобы вычислить норму функционала, рассмотрим линейную оболочку L = span{x} вектора х и определим на ней линейный функционал по формуле l(lх) = l||x|| при всех lÎR. В силу следствия из теоремы Хана-Банаха этот функционал имеет продолжение h Î Е* с нормой ||h|| = ||l||L = 1. Так как ax(h ) = h(x) = l(x) = ||x||, |ax(f )| £ ||x|| для всех fÎ S*, то ||ax|| = ||x||. Следовательно, имеет ме­сто равенство ||J(x)|| = ||x|| при всех х ÎЕ. Таким образом, отображение J :Е → Е** изометрично.

Отображение двойственности J : Е ® Е** называется также естественным вложением во второе сопряженное пространство. Каждый элемент х Î Е можно отожде­ствить с ограниченным функционалом J(x) = ax ÎЕ** на сопряженном пространстве Е*.

Поэтому очень часто вводится симметричное обозначение для зна­чений функционала f(x) = (f, x), где х ÎЕ и f ÎE*. Выра­жение вида (f, x) можно рассматривать как непрерывную билинейную форму на прямом произведении Е*´Е.

В самом деле, линейность по f и по х следует из ее определения, а непрерывность вытекает из неравенств

|(f , x) – (g, y)| £ |(f – g, x)| + |(g, x – y)| £ ||f – g||×||x|| +||g||×||x – y||.

Эта двойственность между векторами и функционалами проявляется также в следующих формулах:

.

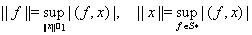
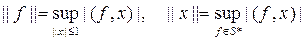В случае, если образ вложения ImJ совпадает с пространством E** нормированное пространство Е называется рефлексивным.

Далее будут рассмотрены примеры сопряженных для конкретных банаховых пространств. Будет отмечена их рефлексивность или нерефлексиность.

Исследование, описанное в статье про 2. Сопряженные пространства, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 2. Сопряженные пространства и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ