Привет, Вы узнаете о том , что такое 1. Линейные пространства. Нормированные пространства. Метрика, порожденная нормой. Ряды в нормированных пространствах. Абсолютная сходимость ряда и полнота нормированного пространства. Факторпространства, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 1. Линейные пространства. Нормированные пространства. Метрика, порожденная нормой. Ряды в нормированных пространствах. Абсолютная сходимость ряда и полнота нормированного пространства. Факторпространства , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Линейным (или векторным) пространством называется множество X, для которого определены операции сложения x+y и умножения векторов на числа lx, обладающие следующими свойствами:

1) x+y=y+x;

2) (x+y)+z=y+(x+z);

3) Существует такой элемент (нулевой) 0ÎX, что x+0=x для любого x;

4) Для всякого xÎX существует обратный (-x), т.е. такой, что x+(-x)= 0;

5) (lm)x=l(mx)

6) (l+m)x=lx+mx;

7) l(x+y)=lx+ly

8) 1×x=x.

Векторы x1, x2,…, xn называются линейно независимыми, если из равенства l1x1 + l2x2 +…+ lnxn = 0 следует, что l1 = l2 =…= ln = 0. В противном случае векторы называются линейно зависимыми. Линейное пространство называется n-мерным, если в нем существует п линейно независимых векторов, а любая система из большего числа векторов является линейно зависимой.

Любой набор из п линейно независимых векторов в n-мерном пространстве называется базисом линейного пространства. Всякий вектор п-мерного пространства представим единственным образом в виде линейной комбинации l1x1 + l2x2 +…+ lnxn по базису {x1,…, xn}. Если в линейном пространстве существует сколь угодно много линейно независимых векторов, то пространство называется бесконечномерным.

Множество векторов в X, замкнутое относительно операций сложения и умножения на числа, называется линейным многообразием. Множество векторов М, которое вместе с любыми двумя точками содержит прямую, проходящую через них, называется аффинным многообразием. Если x и y – две точки из М, то любая точка прямой, проходящей через x и y представима в виде lx +my при некоторых числах l, m таких, что l + m = 1. Аффинное многообразие, содержащее нулевой вектор, является линейным многообразием. Линейное многообразие всегда является аффинным многообразием.

Множество М в линейном пространстве называется выпуклым, если вместе с любыми двумя точками оно содержит соединяющий их отрезок. Если x и y – две точки из М, то любая точка отрезка, соединяющего x и y представима в виде lx +my при некоторых числах l, m таких, что l, m ³ 0, l + m = 1. Отрезок с концами x и y обозначается [x, y].

Определение 1. Множество E называется линейным нормированным пространством, если

1. E - линейное пространство с умножением на вещественные (комплексные) числа.

2. Каждому элементу x линейного пространства E ставится в соответствие вещественное число, которое называется нормой этого элемента и обозначается 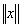, причем предполагается, что норма элемента удовлетворяет следующим условиям (аксиомам нормы)

1) ³ 0, причем 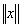= 0 лишь если x = 0 (нуль векторного пространства);

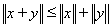
2) 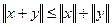(неравенство треугольника для норм)

3)

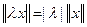
В случае, когда рассматриваются несколько нормированных пространств, указание в каком пространстве рассматривается норма, осуществляется следующим образом: ||x|X||, ||y|Z|| и т.д.

В линейном нормированном пространстве можно ввести метрику посредством равенства

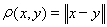
Легко проверить, что введенное расстояние удовлетворяет всем аксиомам метрики. После введения метрики определяется сходимость последовательности элементов {xn} к x, а именно

x=lim xn или , есл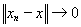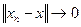и при .

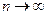Определенная таким образом сходимость в линейном нормированном пространстве называется сходимостью по норме.

Если линейное нормированное пространство является полным в смысле сходимости по норме, то оно называется банаховым пространством.

Пример 1. n-мерное векторное пространство является банаховым пространством, с нормой

= ,

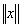
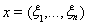
причет метрика, порожденная нормой, в этом пространстве совпадает с ранее введенной в Rn метрикой.

Пример 2. С[a, b] есть банахово пространство с нормой

= ,

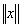
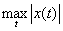
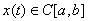
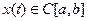
Метрика полученного пространства совпадает с метрикой, ранее введенной в C[a, b].

Пример 3. Об этом говорит сайт https://intellect.icu . 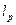есть банахово пространство с нормой

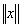
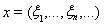
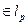= , , 1£ p < ¥

Метрика полученного пространства совпадает с прежней метрикой.

Пример 4. Lp[a, b] есть банахово пространство с нормой, 1£ p < ¥

= , .

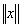
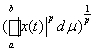
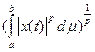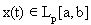
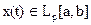Свойство треугольника нормы вытекает из неравенства Минковского (см. Приложение). Полнота этого пространства будет установлена в главе 8.

Пример 5. Сk[a, b] – есть банахово пространство с нормой

= .

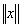
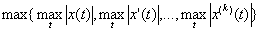
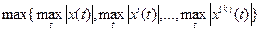Пример 6. m – банахово пространство, с нормой

= ,

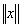
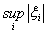
метрика в котором совпадает с метрикой, введенной ранее.

Пример 7. L¥[a, b] – банахово пространство измеримых, п.в. ограниченных функций с нормой

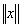
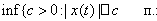
= = ess sup |x(t)|.

Полнота этого пространства будет доказана в главе 8.

Не все ранее рассмотренные метрические пространства являются нормированными. Нельзя ввести норму, порождающую ту же топологию, что и метрика, например, в пространстве числовых последовательностей s.

Отметим непрерывность основных линейных операций в линейном нормированном пространстве, а именно:

Если xn ® x, yn ® y, ln ® l, то тогда xn + yn ® x + y, lnxn ® lx. Это следует из соотношений

+ .

+ .

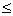
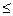
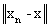
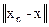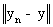
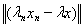
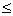
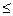
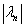
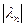
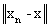
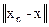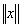
Далее нетрудно видеть, что если xn ® x, то ||xn|| ® ||x||, и, в частности, ||xn|| есть ограниченная числовая последовательность. Это вытекает из обратного неравенства треугольника:

| ||x|| - ||y|| | £ ||x – y||,

легко вытекающего из неравенства треугольника.

Так как линейное нормированное пространство есть метрическое пространство, то для такого пространства имеют смысл все понятия, введенные в метрических пространствах (шар, ограниченное множество, компактность, сепарабельность и т.д.), а также имеют место все теоремы, доказанные для таких пространств.

Для банаховых пространств будет справедливым все, что было ранее установлено для полных метрических пространств.

Пусть L – линейное многообразие линейного нормированного пространства Е. Если L , кроме того, является замкнутым множеством, то L называется подпространством.

Если L – конечномерное линейное многообразие линейного нормированного пространства, то, как мы увидим ниже, 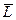=L . Для бесконечных линейных многообразий это равенство может не иметь место.

Пример 8. Пусть E = C[a,b] и L – линейное многообразие, порожденное элементами

x0 = 1, x1 = t, …, xn = tn,…

Тогда L – множество всех многочленов. При этом в силу теоремы Вейерштрасса

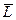= C[a,b]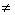 L.

Пусть x1, x2, …, xn, … – элементы нормированного пространства Е. Выражение вида 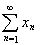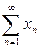назовем рядом, составленным из элементов пространства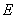 . Этот ряд называется сходящимся и имеет сумму х, если последовательность частных сумм 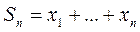сходится по норме к х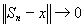 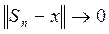при .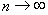

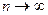Для рядов в нормированных пространствах вводится понятие абсолютной сходимости: если сходится числовой ряд

.

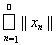
В нормированных пространствах справедлив следующий признак полноты пространств.

Теорема 1. Для того чтобы нормированное пространство Х было полным необходимо и достаточно, чтобы из абсолютной сходимости ряда вытекала его сходимость.

Необходимость. В силу полноты пространства Х для сходимости последовательности 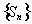достаточно, чтобы она была фундаментальной. Но это с очевидностью следует из неравенства

,

где последняя оценка вытекает из критерия Коши сходимости числового ряда .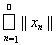

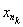
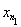
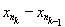
Достаточность. Рассмотрим произвольную фундаментальную последовательность xn в Х. В силу фундаментальности этой последовательности для e = 1/2k найдется номер nk такой, что при n, m ³ nk выполняется неравенство ||xn – xm|| < 1/2k. Возьмем подпоследовательность и построим по ней последовательность y1 = , yk = . В силу оценки ||yk|| = || 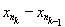|| < 1/2k, ряд 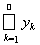сходится абсолютно, а следовательно и сходится. Тогда частичные суммы этого ряда Sm = 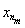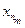сходятся. Итак, взятая нами фундаментальная последовательность имеет сходящуюся подпоследовательность. В силу леммы 2.4 и сама последовательность сходится.

Пусть X – нормированное пространство, а М – подпространство в X. Введем на Х отношение эквивалентности, полагая х ~ у если х - у Î М. Элементы пространства X разобьем на непе­ресекающиеся классы эквивалентности [х], [z], ... Элемент х Î [х] будем назы­вать представителем класса [х]. Если х — представитель класса [х], то любой другой представитель [х] будет иметь вид х + z, где z Î М. Множество всех таких классов называется фактор-пространством пространства X по подпространству М и обозначается 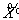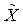= Х/М.

Введем в 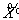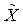операции сложения классов и умножения класса на число. Пусть х Î [х], у Î [у], тогда класс [х] + [у] определим как класс, представителем которого является элемент х + у. Далее, класс а[х], где а – число, определим как класс, содержащий ах.

Введем в 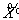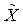норму по формуле

||[x]|| = .

Аксиомы нормы проверяются достаточно несложно (проверьте!). Итак, 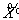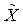– нормированное пространство.

Теорема 2. Если X полное, то и 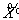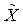полное.

Доказательство. Покажем сначала, что если последователь­ность {[х]n} Ì 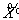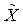фундаментальна в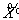 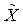, то найдется последовательность номеров {n(k)} такая, что соответствующая ей подпоследовательность представителей {хn(k)} Ì X (хn(k) Î [х] n(k)) сходится в X.

Действительно, возьмем n(k) такими, чтобы ||[x]n(k + 1) – [x]n(k)|| < 1/2k, k = 1, 2, ... Из определения нормы в 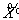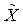следует существование zk Î [x]n(k + 1) – [х]n(k) таких, что ||zk|| < 1/2k, k = 1, 2, ... Рассмотрим в X сходящийся ряд хn(1) + z1 + z2 + ... и пусть х — его сумма. По построе­нию хn(k) ® х, k ® ¥ и

Отсюда и из фундаментальности {[х]n} заключаем, что [х]n(k) ® [x], где [х] – класс, содержащий х. Теорема доказана.

Исследование, описанное в статье про 1. Линейные пространства. Нормированные пространства. Метрика, порожденная нормой. Ряды в нормированных пространствах. Абсолютная сходимость ряда и полнота нормированного пространства. Факторпространства, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 1. Линейные пространства. Нормированные пространства. Метрика, порожденная нормой. Ряды в нормированных пространствах. Абсолютная сходимость ряда и полнота нормированного пространства. Факторпространства и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ