1. Измеримые функции и их свойства кратко

Привет, Вы узнаете о том , что такое 1. Измеримые функции и их свойства, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 1. Измеримые функции и их свойства , настоятельно рекомендую прочитать все из категории Функциональный анализ.

В классическом анализе используются главным образом непрерывные или кусочно-непрерывные функции. В современном функциональном анализе применяются так называемые измеримые функции. Класс этих функций достаточно широк и в основном он удовлетворяет потребностям анализа.

Рассмотрим измеримое пространство (X, S, m) со счетно-аддитивной полной мерой m.

Определение 1. Пусть Е ÎS. Действительная функция f: E ® R называется измеримой на множестве Е, если лебеговы множества этой функции:

Е(f < с) = {хÎЕ: f(х) < с}

измеримы, т. е. E(f <с) Î S при всех с Î R.

Из этого определения, в частности, сразу следует, что если Х = R и S – алгебра измеримых функций по мере на числовой прямой, то любая непрерывная функция является измеримой. Это вытекает из определения непрерывных функций (определение 1.18): если полный прообраз f -1(V) любого открытого множества V является открытым множеством.

Поскольку система S есть s-алгебра, то из условия измеримости всех лебеговых множеств E(f <с) вытекает измеримость следующих множеств:

E(f³c) = E\E(f<c); E(f£c) = 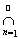E(f < c + 1/n); E(f>c) = E\E{f£c); E{a £ f < b) = E(f < b) \E(f < a);

E(a < f < b ) = E(f < b)\E(f £ a); E{a < f £ b) = E(f £ b) \E(f £ a); E{a £ f £ b) = E(f £ b) \E(f < a).

Отметим, что измеримые функции могут принимать и бесконечные значения. Поэтому также измеримыми являются множества:

E(f = +¥) = 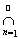E(f > n); E(f = -¥) = X\ 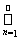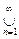E(f < -n).

Обозначим через t систему всех открытых множеств на прямой R и рассмотрим минимальную s-алгебру, содержащую все открытые множества t. Напомним (определение 3.28), что множества А, принадлежащие этой s-алгебре, называются борелевскими. Так как дополнение открытого множества является замкнутым, то все открытые и замкнутые мно­жества являются борелевскими. В том числе все проме­жутки на прямой (отрезки, интервалы и полуинтервалы) являются борелевскими множествами.

Теорема 1. Функция f: Е® R измерима тогда и только тогда, когда прообраз любого борелевского множества является измеримым, т. е. имеет место включение f –l(A) Î S для всех борелевских множеств. А Ì R.

Доказательство. Достаточность очевидна, так как все интервалы (-¥; c) являются борелевскими множествами. Докажем необходимость.

Предположим, что функция f измерима, и обозначим через X систему множеств А Ì R, у которых прообраз f- -1(А) измерим. Так как S является s-алгеброй и

f -1(A\B) = f -1(A)\ f -1(B), ,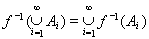

то X есть s-алгебра. Об этом говорит сайт https://intellect.icu . По предположению (см. выше) все множества вида f -1(a, b) = E(a< f < b) измеримы и сле­довательно система X содержит все интервалы (а, b). Поскольку каждое открытое множество из R является объединением не более, чем счетного числа интервалов, то t Ì X. Поэтому в силу минимальности борелевской s-алгебры справедливо включение в X всех борелевских множеств.

Для доказательства измеримости функции f, задан­ной на сумме E = 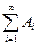конечного или счетного числа измеримых множеств, достаточно проверить ее измери­мость на каждом множестве Аi. Заметим, что измери­мость функции f на множестве Е влечет ее измеримость на каждом измеримом подмножестве А Ì Е.

Лемма 1. Пусть функции f(x) и g(x) измеримы на множестве Е, а функция двух действительных пере­менных h(u,v) непрерывна на открытом множестве D Ì R2, при этом (f(x),g(x)) Î D для всех х ÎЕ. Тогда сложная функция F(x) = h(f(x), g(x)) является измеримой на множестве Е.

Доказательство. В силу непрерывности функции h(u,v) множество D(h < с) является открытым в R2. Поэтому его можно представить в виде конечного или счетного объединения открытых прямоугольников (теорема 3.12):

D(h < с) = 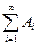, Аi = (ai, bi) ´ (ci, di).

Заметим, что E((f, g) Î Аi) = E(аi < f < bi) ÇE(сi < g < di) есть измеримое множество. Отсюда множество E(F < c) = 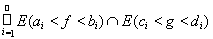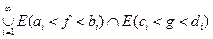будет также измеримым, поскольку система множеств Е является s-алгеброй.

Из этой леммы получаются следующие свойства.

Следствие 1. Пусть функции f и g измеримы на Е. Тогда их сумма f + g и произведение fg измеримы на Е. Частное f/g измеримо, если g(x) ¹ 0 при всех х Î Е. Степень |f|p измерима при всех р > 0.

Утверждение легко вытекает из леммы и непрерывности соответствующих функций u + v, uv и т.д.

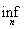
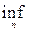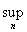
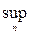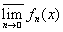
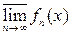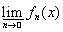
Следствие 2. Пусть последовательность {fn} состоит из изме­римых на множестве Е функций. Если функции вида fn(x), fn(x), , 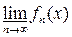принимают конечные значения на Е, то они измеримы.

Если предел функций f(x) = 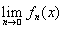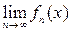существует при всех х Î Е, то f является измеримой функцией.

Измеримость нижней и верхней грани последователь­ности функций доказывается применением следующих соотношений:

E( 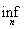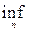fn < c) =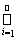 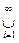E(fn < c),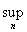 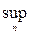fn(x) = –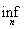 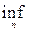(– fn(x)).

Так как при всех х Î Е справедливы равенства

= , = ,

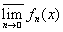
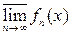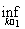
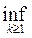
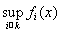
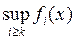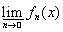
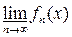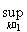
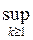
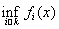
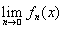
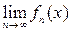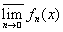
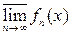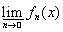
то верхний и нижний пределы будут также измеримыми. Отсюда предел последовательности измеримых функций f = = = 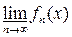является измеримым.

Исследование, описанное в статье про 1. Измеримые функции и их свойства, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 1. Измеримые функции и их свойства и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ