5. Изоморфизм и изометрия сепарабельных гильбертовых пространств. Общий вид линейного функционала в гильбертовом пространстве. Теорема Рисса-Фишера. кратко

Привет, Вы узнаете о том , что такое 5. Изоморфизм и изометрия сепарабельных гильбертовых пространств. Общий вид линейного функционала в гильбертовом пространстве. Теорема Рисса-Фишера., Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 5. Изоморфизм и изометрия сепарабельных гильбертовых пространств. Общий вид линейного функционала в гильбертовом пространстве. Теорема Рисса-Фишера. , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Рассмотрим сепарабельное бесконечномерное гильбертово пространство H, и пусть 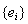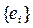– полная ортонормальная система векторов в этом пространстве. Если х – некоторый элемент из H, то этому элементу можно сопоставить в соответствие последовательность чисел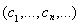 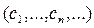, являющихся коэффициентами Фурье вектора х по системе .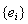

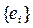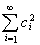
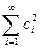Как было показано в п.45 гл.56, ряд сходится, и, следовательно, последовательность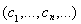 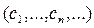можно рассматривать как некоторый элемент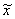 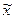гильбертова пространства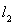 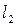. Таким образом, каждому элементу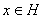 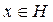соответствует некоторый элемент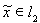 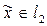, причем в силу условия полноты системы

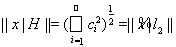
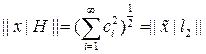. (1)

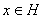
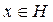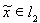
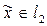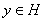
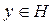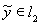
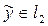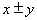
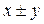Далее очевидно, что если соответствует и соответствует , то и 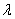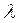x соответствует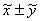 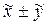и l 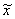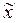, где l – вещественное число. Отсюда и из (1) следует:

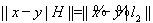
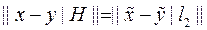. (2)

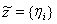
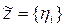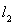
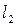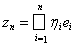
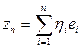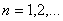
Пусть теперь – произвольный элемент из . Рассмотрим в H элементы , 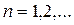. Имеем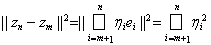 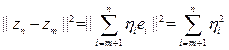, и потому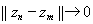 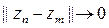при .

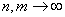
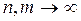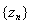
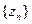Таким образом, последовательность фундаментальна. В силу полноты H она сходится в смысле метрики пространства H к некоторому элементу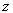 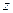этого пространства. Так как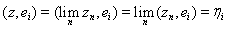 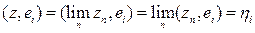, то коэффициенты Фурье элемента z по ортонормальной системе есть числа 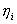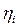. Таким образом, каждый элемент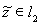 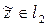соответствует некоторому элементу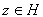 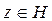. Об этом говорит сайт https://intellect.icu . Тем самым, мы установили взаимно однозначное соответствие между элементами пространств H и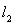 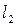. Формула (2) показывает, что это соответствие между H и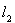 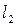.является изометрией. Учитывая ранее сказанное относительно сохранения операций сложения и умножения на число при рассматриваемом соответствии, получаем, что H и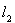 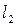изометрически изоморфны. Таким образом, нами доказаны следующая теорема.

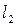Теорема 9. Всякое (вещественное) сепарабельное бесконечномерное гильбертово пространство изометрично и изоморфно (вещественному) пространству и, следовательно, все вещественные сепарабельные гильбертовы пространства изометричны и изоморфны между собой.

Следствие. Вещественные пространства 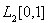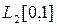и и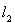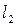зометричны и изоморфны.

Найдем общий вид линейного функционала в гильбертовом пространстве.

Рассмотрим в гильбертовом пространстве H два элемента, x и y, и скалярное произведение этих элементов 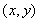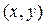. Если мы зафиксируем вектор y и будем менять вектор x, то получим некоторый функционал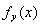 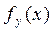, определенный на H: .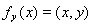

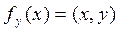Из аддитивности и непрерывности скалярного произведения следует, что 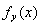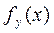– линейный функционал в H. Выбирая различные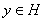 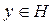, мы будем получать различные линейные функционалы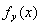 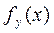. Покажем, что таким образом мы получим все линейные функционалы.

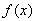
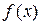Теорема 10 (Рисса-Фишера). Всякий линейный функционал , определенный на гильбертовом пространстве H, имеет вид

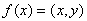
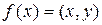, (3)

где элемент 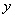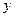однозначно определяется функционалом f. При этом .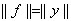

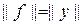Доказательство. Рассмотрим подпространство 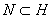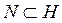, определяемое уравнением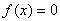 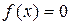(ядро функционала). Замкнутость N следует из непрерывности функционала .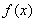

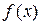Если 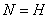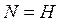, т. е.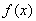 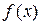тождественно равен нулю, мы можем написать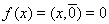 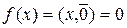, и в этом случае равенство (3) доказано.

Пусть теперь 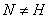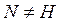; возьмем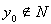 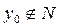, и обозначим через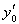 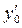проекцию элемента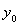 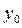на ортогональное дополнение М подпространства N. Пусть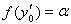 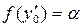. (ясно, что a ¹ 0). Тогда, полагая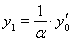 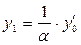, будем иметь .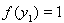

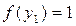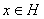
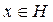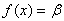
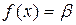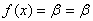
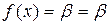
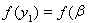
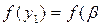
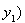
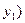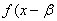
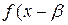
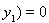
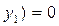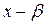
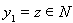
Возьмем любой элемент , и пусть . Имеем , откуда , т. е. 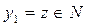. Поэтому любой вектор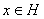 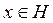имеет вид

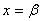
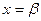
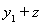
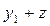, (4)

т. е. H есть ортогональная сумма подпространства N и одномерного подпространства M, порождаемого элементом 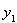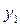. Из равенства (4), умножая скалярно на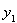 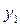, получаем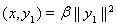 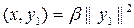(y1ÎN^ = M, z ÎN), или

.

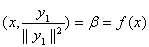
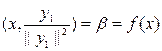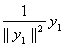
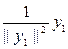Обозначая через 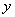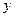, будем иметь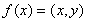 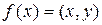, и равенство (3) доказано.

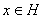
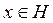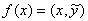
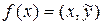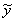
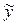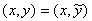
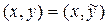Если, теперь при всех верно равенство для некоторого другого элемента , то или 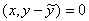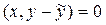при любом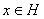 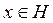. В частности полагая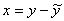 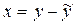, получим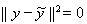 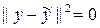, т. е.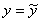 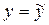и однозначность представления линейного функционала в виде скалярного произведения доказана.

Из неравенства Коши-Буняковского при 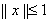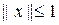, получим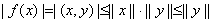 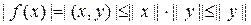, поэтому и

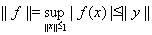
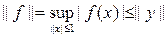. (5)

С другой стороны, если 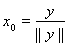, то мы будем иметь

,

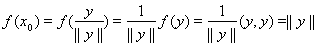
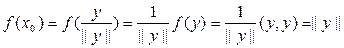и так как 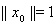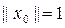, то

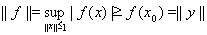
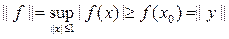. (6)

Из сравнения (5) и (6) следует, что 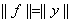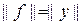, и теорема полностью доказана.

Как частные случаи этой теоремы, получаем

а) Всякий линейный функционал в L2[a, b] имеет вид

,

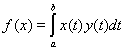
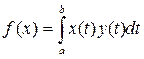где 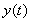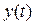также принадлежит L2[a, b], причем

.

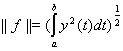
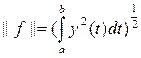б) Всякий линейный функционал в 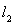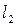имеет вид

,

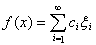
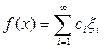где 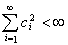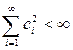, причем .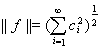

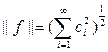Исследование, описанное в статье про 5. Изоморфизм и изометрия сепарабельных гильбертовых пространств. Общий вид линейного функционала в гильбертовом пространстве. Теорема Рисса-Фишера., подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 5. Изоморфизм и изометрия сепарабельных гильбертовых пространств. Общий вид линейного функционала в гильбертовом пространстве. Теорема Рисса-Фишера. и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ

Из статьи мы узнали кратко, но содержательно про