4. Предельный переход под знаком интеграла кратко

Привет, Вы узнаете о том , что такое 4. Предельный переход под знаком интеграла, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 4. Предельный переход под знаком интеграла , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Здесь мы рассмотрим следующий вопрос: пусть на измеримом множестве E задана последовательность измеримых функций

f1(x), f2(x), f3(x), ¼ , fn(x), ¼

которая в каком-нибудь смысле (всюду, почти всюду, по мере) схо­дится к измеримой функции F(x). Спрашивается, будет ли справедливо соотношение

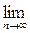
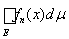
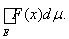
= (3)

Если (3) верно, то говорят, что допустим предельный переход под знаком интеграла.

Легко видеть, что, вообще говоря, это не так. Например, если функции fn(x) определены на отрезке [0, 1] следующим образом:

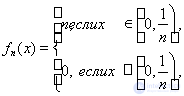
то при всяком x Î [0, 1] будет 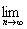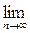fn(x) = 0, но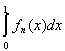 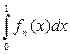= 1, и этот интеграл не стремится к нулю.

Поэтому естественно поставить вопрос о тех дополнительных ограничениях, которые нужно наложить на функцию fn(x), чтобы равенство (3) все же имело место.

Теорема 13 (Лебега о монотонной сходимости). Пусть на измеримом множестве Е за­дана последовательность f1(x), f2(x), f3(x), ¼ неотрицательных измеримых функций, монотонно сходящаяся к измеримой функции F(х): fn(x)­ F(х). Тогда справедливо равенство

=

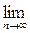
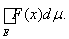
Доказательство. В силу монотонности интеграла существует конечный или бесконечный предел

I = .

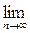
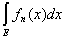
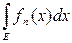Из неравенства fn(x) £ F(х) на множестве Е вытекает, что I £ . Об этом говорит сайт https://intellect.icu . Докажем обратное неравенство.

Пусть простая неотрицательная измеримая функция h выбрана так, что h £ F(х) на множестве Е. Возьмем произвольное число 0 < l < 1 и определим множества Еi = {x Î E: lh(x) £ fi(x)}. Тогда Ei Ì Ei + 1 и 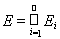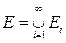. Отсюда следует неравенство

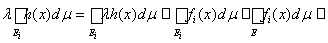
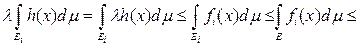I.

Обозначим Е0 = Æ, тогда справедливо представление 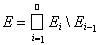. В силу свойства счетной аддитивности интеграла (теорема 12)

.

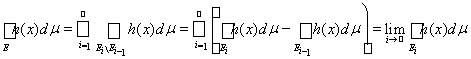
Следовательно, переходя к пределу в доказанном выше неравенстве 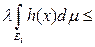I вначале при i ® ¥, а затем при l ® 1, получим неравенство 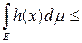I. Отсюда по теореме 9 имеем неравенство I, что и доказывает теорему.

Лемма 4 (Фату). Пусть на измеримом множестве Е за­дана последовательность f1(x), f2(x), f3(x), ¼ измеримых неотрицательных функций, имеющая нижний предел 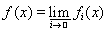. Тогда

.

Доказательство. Определим функции 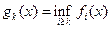на множестве Е. Функции gk(x) являются неотрицательными, измеримыми и монотонно сходятся к f (x) на Е. По теореме о монотонной сходимости

= .

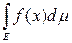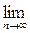
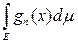Из неравенства при всех i ³ k вытекает

.

Отсюда, переходя к пределу при k ® ¥, получим

.

Таким образом, неравенство доказано.

Теорема 14 (Лебега о мажорантной сходимости). Пусть на измеримом множестве Е за­дана последовательность f1(x), f2(x), f3(x), ¼ измеримых функций, сходящаяся п.в. к измеримой функции F(х). Если существует интегрируемая функция g(x), такая, что при всех п и при всех х выполняется неравенство 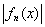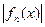£ g(x), то функция F(х) интегрируема на Е и справедливо равенство

=

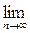
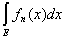
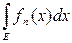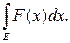
Доказательство. Прежде всего заметим, что почти для всех х Î Е будет 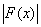£ g(x), а следовательно, F+(х) £ g(x) и (–F–(х)) £ g(x), что по определению 3 и теореме 12 влечет интегрируемость F(х).

Так как g(x) ± fi(x) ³ 0 на множестве Е, то применяя лемму Фату и теорему 12, имеем

,

.

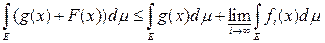Мы здесь воспользовались тем, что g(x) ± fi(x) ® g(x) ± F(х) и тем, что верхний и нижний предел обладают следующим свойством:

,

,

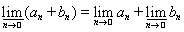
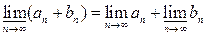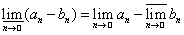
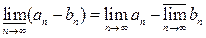в предположении существования предела 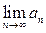. Используя свойства линейности интеграла, приходим к неравенствам

.

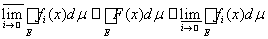
Последние неравенства, в силу свойств нижнего, верхнего и обычного предела, доказывают теорему.

Исследование, описанное в статье про 4. Предельный переход под знаком интеграла, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 4. Предельный переход под знаком интеграла и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ

Из статьи мы узнали кратко, но содержательно про