Лекция
Привет, Вы узнаете о том , что такое самосопряженный оператор, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое самосопряженный оператор , настоятельно рекомендую прочитать все из категории Функциональный анализ.
В математике оператор в комплексном или действительном гильбертовом пространстве
называется эрмитовым, симметрическим, если он удовлетворяет равенству
для всех
из области определения
. Здесь и далее полагается, что
— скалярное произведение в
. Название дано в честь французского математика Шарля Эрмита.
Оператор в называется самосопряженным, или гипермаксимальным эрмитовым, если он совпадает со своим сопряженным.
Сопряженный оператор — обобщение понятия эрмитово-сопряженной матрицы для бесконечномерных пространств. самосопряженный оператор является симметрическим; обратное, вообще говоря, не верно. Для непрерывных операторов, определенных на всем пространстве, понятия симметрический и самосопряженный совпадают.
Определение 4. Линейный ограниченный оператор А в гильбертовом пространстве Н называется самосопряженным или симметрическим, если он совпадает со своим сопряженным: А = А*.
Иными словами, самосопряженный оператор А характеризуется условием (Ax, y) = (x, Ay) для  . В последнем примере, если ядро K(t, s) симметрическое: K(t, s) = K(s, t), то
. В последнем примере, если ядро K(t, s) симметрическое: K(t, s) = K(s, t), то

и значит, интегральный оператор будет симметрическим.
Нетрудно видеть, что любая линейная комбинация самосопряженных операторов также является самосопряженным оператором.
Таким образом, в линейном нормированном пространстве линейных операторов, отображающих Н в Н, самосопряженные операторы составляют линейное многообразие. Кроме того, мы сейчас докажем, что это подмножество замкнуто и, следовательно, является подпространством. Другими словами, если операторы An – самосопряженные и An 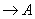 (по норме), то и оператор А – самосопряженный. Докажем даже более сильное утверждение.
(по норме), то и оператор А – самосопряженный. Докажем даже более сильное утверждение.
Теорема 13. Если операторы An – самосопряженные и последовательность {An} точечно сходится к оператору А, то А будет также самосопряженный оператор.
Доказательство. Из непрерывности скалярного произведения следует, что при любых  .
.
(Ах, у) = ( 
 Аnx, y) =
Аnx, y) = 
 (Аnx, y) =
(Аnx, y) = 
 (x, Аny) = (x,
(x, Аny) = (x, 
 Аny) = (x, Ay).
Аny) = (x, Ay).
Теорема доказана.
Если операторы А и В – самосопряженные, то 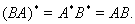 Следовательно, для того, чтобы оператор АВ был самосопряженным, необходимо и достаточно, чтобы
Следовательно, для того, чтобы оператор АВ был самосопряженным, необходимо и достаточно, чтобы 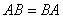 , т.е., чтобы операторы А и В были перестановочны между собой. Об этом говорит сайт https://intellect.icu . В частности, все степени
, т.е., чтобы операторы А и В были перестановочны между собой. Об этом говорит сайт https://intellect.icu . В частности, все степени 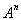 самосопряженного оператора А также есть самосопряженные операторы.
самосопряженного оператора А также есть самосопряженные операторы.
Имеет место следующая важная формула для нормы самосопряженного оператора.
Теорема 14. Если оператор А – самосопряженный, то

Доказательство. По неравенству Коши – Буняковского имеем, при 
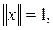
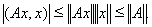
 Следовательно, если
Следовательно, если 
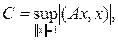 то
то 

Докажем обратное неравенство. Заметим, что любой 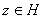 можно представит в виде
можно представит в виде 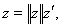
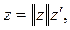 где
где 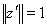
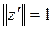 (т.к. если
(т.к. если 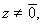
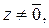 то
то 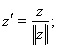
 если
если 
 то
то 
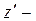 любой вектор с нормой равной единице). Отсюда для любого
любой вектор с нормой равной единице). Отсюда для любого 
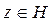 выполнено |(Az, z)| = ||z||2|(Az¢, z¢ )| £ C||z||2.
выполнено |(Az, z)| = ||z||2|(Az¢, z¢ )| £ C||z||2.
Теперь для любых  учитывая равенство
учитывая равенство 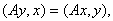 имеем
имеем
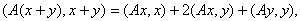

и, вычитая из первого равенства второе, находим

Отсюда, и установленного выше неравенства |(Az, z)| £ C||z||2
|(Ax, y)| £  C(||x + y||2 + ||x – y||2)|.
C(||x + y||2 + ||x – y||2)|.
Воспользуемся равенством параллелограмма (теорема 6.8)
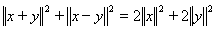 ,
,
получаем
|(Ax, y)| £ 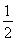 C(||x||2 + ||y||2)|.
C(||x||2 + ||y||2)|.
Полагая 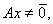 подставим в последнем неравенстве
подставим в последнем неравенстве  . Тогда
. Тогда 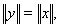 и мы получаем
и мы получаем 
 или
или 
 Это же неравенство верно и при Ах = 0. Следовательно,
Это же неравенство верно и при Ах = 0. Следовательно, 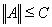 и, тем самым, равенство
и, тем самым, равенство  доказано.
доказано.
Следствие 1. Если для самосопряженного оператора 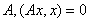 при всех
при всех  то А=0.
то А=0.
Действительно, если  при всех
при всех  то по теореме,
то по теореме,  и значит А = 0.
и значит А = 0.
Для самосопряженного оператора А вводится еще понятие его границ – верхней и нижней:
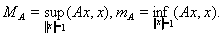

Следствие 2. 
 Из теоремы следует, что
Из теоремы следует, что
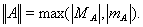
Из определения границ легко выводится, что для любого  имеет место соотношение
имеет место соотношение

1. Являются ли линейными следующие функционалы в C[0, 1]?
1) 
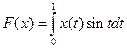 ;
;
2) F(x)=x(1/2);
3) 
 ;
;
4) 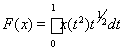
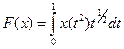
5) 
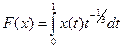 ;
;
6) 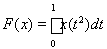
 ;
;
7) F(x)=x¢(t0);
8) 
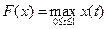 ;
;
9) 
 ;
;
10) 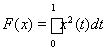
 .
.
Какие из этих функционалов непрерывны в C[0, 1]? Вычислить их нормы.
Какие из этих функционалов непрерывны в L2[0,1]? Вычислить их нормы.
2. Какие из указанных функционалов, действующих на соответствующих классах элементов из l2, будут линейными; непрерывными?
1) f(x)= 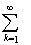
 xksink;
xksink;
2) f(x)= xk;
3) f(x)= 
 xksgn(k-n);
xksgn(k-n);
4) f(x)= 
 xk2k1/2;
xk2k1/2;
5) f(x)= 
 xkk-1/2;
xkk-1/2;
6) f(x)= 
 xk2;
xk2;
7) f(x)= xk-xk-1;
8) f(x)= 
 |xk|;
|xk|;
9) f(x)=supk|xk|;
10) f(x)= 
 |xk| 2.
|xk| 2.
3. Найти норму функционала 
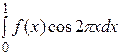 в пространстве C[0, 1].
в пространстве C[0, 1].
4. Непрерывны ли на пространстве 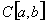
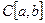 , следующие линейные функционалы
, следующие линейные функционалы
а) 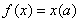
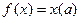 ;
;
б) 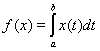
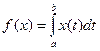 ;
;
5. Проверить, что функционал
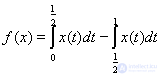
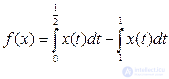
непрерывен в пространстве 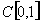 ; показать, что точная верхняя грань его значений в замкнутом единичном шаре пространства С[0,1] равна 1, но эта верхняя грань не достигается ни на каком элементе единичного шара.
; показать, что точная верхняя грань его значений в замкнутом единичном шаре пространства С[0,1] равна 1, но эта верхняя грань не достигается ни на каком элементе единичного шара.
6. Пусть в гильбертовом пространстве последовательность {хn} слабо сходится к х0, т.е. (xn, y) ® (x0, y) для любого y ÎH, и ||хn|| ® ||х0||. Показать, что хn ® х0.
7. Если в гильбертовом пространстве последовательность {хn} слабо сходится к х0 и последовательность {yn} сходится по норме к y0, то (хn, yn) ® (х0, y0). Достаточно ли слабой сходимости последовательности {yn}?
8. Докажите, что в конечномерном пространстве слабая сходимость совпадает с сильной, т.е. сходимостью по норме.
Исследование, описанное в статье про самосопряженный оператор, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое самосопряженный оператор и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ
Из статьи мы узнали кратко, но содержательно про самосопряженный оператор
Комментарии
Оставить комментарий
Функциональный анализ
Термины: Функциональный анализ