Лекция
Привет, Вы узнаете о том , что такое 6. Заряды. Теорема Радона—Никодима, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 6. Заряды. Теорема Радона—Никодима , настоятельно рекомендую прочитать все из категории Функциональный анализ.
Определение 5. Пусть S — s-алгебра с единицей X, а Ф — счетно аддитивная действительнозначная функция на М. Тогда Ф называется зарядом.
Определение 6. Пусть заряд Ф задан на s-алгебре S с единицей Х и множество А ÎS. Тогда множество А называется положительным (отрицательным) относительно Ф, если для любого множества В ÎS, В Ì А выполнено неравенство Ф(В) ³ 0 (Ф(В) £ 0).
Отметим, что для пустого множества в силу аддитивности заряда Ф(Æ) = 0, и пустое множество одновременно является положительным и отрицательным.
Лемма 5. Пусть Ф — заряд на s-алгебре S с единицей X, и пусть существует такое множество В ÎS, что Ф(В) < 0. Тогда найдется отрицательное множество Во ÎS, Во Ì В, Ф(В0) < 0.
Доказательство. Если для любого A ÎS и А Ì В имеем Ф(А) £ 0, то В само отрицательно. Предположим, что l(В) = 
 > 0. Сначала предположим, что l(В) = +¥. Тогда можно выбрать измеримое множество А1 Ì В так, что Ф(А1) > 1. При этом если В1 = В\А1, то Ф(В1) < Ф(В) < 0. Если l(В1) < ¥, то процесс заканчивается, а если нет, то можно выбрать измеримое А2 Ì В1 так, что Ф(А2) > 1, и т. д. Предположим, что процесс этот бесконечен. Тогда мы получим последовательность попарно непересекающихся измеримых множеств А1, А2,... с Ф(Аk) > 1 при k = 1, 2,... Но в этом случае
> 0. Сначала предположим, что l(В) = +¥. Тогда можно выбрать измеримое множество А1 Ì В так, что Ф(А1) > 1. При этом если В1 = В\А1, то Ф(В1) < Ф(В) < 0. Если l(В1) < ¥, то процесс заканчивается, а если нет, то можно выбрать измеримое А2 Ì В1 так, что Ф(А2) > 1, и т. д. Предположим, что процесс этот бесконечен. Тогда мы получим последовательность попарно непересекающихся измеримых множеств А1, А2,... с Ф(Аk) > 1 при k = 1, 2,... Но в этом случае 
 , и мы приходим к противоречию (заряд по определению должен всюду на S принимать конечные значения). Поэтому для некоторого k получим, что l(Вk) < ¥, причем Ф(Bk) < 0. В этом случае будем искать удовлетворяющее условиям леммы множество В0 среди измеримых подмножеств множества Вk. В дальнейшем, не ограничивая общности, считаем, что 0 < l(В) <¥.
, и мы приходим к противоречию (заряд по определению должен всюду на S принимать конечные значения). Поэтому для некоторого k получим, что l(Вk) < ¥, причем Ф(Bk) < 0. В этом случае будем искать удовлетворяющее условиям леммы множество В0 среди измеримых подмножеств множества Вk. В дальнейшем, не ограничивая общности, считаем, что 0 < l(В) <¥.
Выберем измеримое множество А1 Ì В так, чтобы Ф(А1) > l(В)/2, и пусть В1 = В\А1. Тогда Ф(В1) < Ф(В) и l(В1) < l(В)/2. Если l(В1) = 0, то можно взять B0 = B1, в противном случае можно повторить изложенную выше операцию. В итоге либо на некотором шаге будет найдено отрицательное подмножество В, либо мы построим цепочку таких вложенных измеримых множеств В É В1 É В2 É ..., что Ф(Вj + 1) < Ф(Вj) и l(Bj) £ l(B)/2j при j = 1, 2,... В этом случае можно взять 
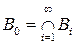 .
.
Напомним (теорема 3.4), что заряд счетно аддитивен тогда и только тогда, когда он непрерывен: Ф(В0) = 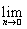
 Ф(Вn). Тогда Ф(В0) < Ф(В), а из неравенства l(Bj) £ l(B)/2j следует, что не существует измеримого множества А Ì В0 с Ф(А) > 0.
Ф(Вn). Тогда Ф(В0) < Ф(В), а из неравенства l(Bj) £ l(B)/2j следует, что не существует измеримого множества А Ì В0 с Ф(А) > 0.
Теорема 19. Пусть Ф –заряд на s-алгебре S с единицей X. Тогда существует такое множество А+ ÎS, что оно положительно, а множество А_ = Х\А+ – отрицательно относительно заряда Ф. Представление X = А+ + А_ называется разложением Хана заряда Ф.
Доказательство. Обозначим множество всех отрицательных множеств A ÎS через S_ и положим 
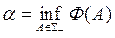 . Будем считать, что a <0, иначе доказывать нечего (отрицательных множеств вообще нет). Пусть последовательность множеств
. Будем считать, что a <0, иначе доказывать нечего (отрицательных множеств вообще нет). Пусть последовательность множеств 
 из S_ такова, что
из S_ такова, что 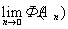
 = a. Тогда множество
= a. Тогда множество 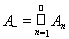
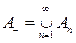 ÎS_ и для любого п выполнено неравенство Ф(А_) £ Ф(Аn) (в силу аддитивности заряда), откуда Ф(А_) = a (поэтому, в частности, a > –¥).
ÎS_ и для любого п выполнено неравенство Ф(А_) £ Ф(Аn) (в силу аддитивности заряда), откуда Ф(А_) = a (поэтому, в частности, a > –¥).
Докажем, что множество А+ = Х\А_ положительно. Если это не так, то существует измеримое В Ì А+ с Ф(В) < 0. Согласно лемме 5, можно выбрать отрицательное множество В0 Ì В с Ф(В0) < 0. Об этом говорит сайт https://intellect.icu . Но в этом случае множество С = А_ + В0 отрицательно и Ф(С) <Ф(А_) = a. Полученное противоречие доказывает теорему.
Установим единственность, в соответствующем смысле, разложения Хана.
Лемма 6. Пусть Ф – заряд на s-алгебре S с единицей X и В+ + В_ = X = А+ + А_ – два разложения Хана. Тогда для любого Е ÎS имеем Ф(ЕÇА+) = Ф(ЕÇВ+) и Ф(ЕÇА_) = Ф(ЕÇВ_).
Доказательство. Поскольку множество ЕÇ(А+\В+) одновременно является подмножеством и А+ и В_, Ф(ЕÇ(А+ \ В+)) = 0. Аналогично, Ф(ЕÇ(В+ \ А+)) = 0. Поэтому Ф(ЕÇА+) = Ф(ЕÇ(А+ ÇВ+)) = Ф(ЕÇВ+). Аналогично устанавливается второе равенство.
Определение 7. Если Ф — заряд на s-алгебре S с единицей X и X = А++А_ –разложение Хана, то можно однозначно определить две s-аддитивные меры Ф+(Е) = Ф(ЕÇА+) и Ф–(Е) = –Ф(ЕÇА_). Разложение Ф = Ф+ – Ф– называется разложением Жордана заряда Ф, а мера Ф = Ф+ + Ф– – полной вариацией исходного заряда.
Определение 8. Пусть (X, S, m) — s-конечное измеримое пространство, а Ф – заряд на S. Тогда Ф называется абсолютно непрерывным относительно меры m, если из того что Е ÎS и m(Е) = 0, вытекает, что Ф(Е) = 0.
Лемма 7. Пусть (X, S, m) – конечное измеримое пространство, а Ф – s-аддитивная мера на S, абсолютно непрерывная относительно меры m, и Ф не равен тождественно нулю. Тогда существуют такое натуральное число n и такое множество В ÎS, что m(В) > 0 и В положительно относительно заряда yn = Ф 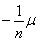
 .
.
Доказательство. Пусть X = A+(i) + A_(i) – разложение Хана относительно заряда yi, где i = 1, 2,... При этом можно считать, что А+(1) Ì А+(2) Ì ... Далее, пусть 
 и
и 
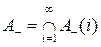 . Очевидно, что X = А+ ÈА_. Тогда для любого m имеем ym(А_) <0, т. е. Ф(А_) £
. Очевидно, что X = А+ ÈА_. Тогда для любого m имеем ym(А_) <0, т. е. Ф(А_) £ 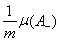
 , откуда Ф(А_) = 0. Поэтому Ф(А+) > 0, а следовательно, и m(А+) > 0. Согласно свойству непрерывности меры найдется такое n, что m(А+(n)) > 0. Но по определению множество А+(n) положительно относительно заряда yn, что и завершает доказательство.
, откуда Ф(А_) = 0. Поэтому Ф(А+) > 0, а следовательно, и m(А+) > 0. Согласно свойству непрерывности меры найдется такое n, что m(А+(n)) > 0. Но по определению множество А+(n) положительно относительно заряда yn, что и завершает доказательство.
Теорема 20 (Радона—Никодима). Пусть (X, S, m) — s-конечное измеримое пространство, а Ф — заряд на S, абсолютно непрерывный относительно меры m. Тогда существует такая интегрируема по Лебегу функция f(x), что для любого А ÎS справедливо равенство
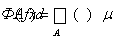
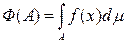 .
.
При этом если для некоторой другой интегрируемой функции g(x) равенство также выполняется для всех А ÎS, то f(x) = g(x) почти всюду относительно меры m.
Доказательство. Благодаря наличию разложения Жордана, достаточно доказать теорему для случая, когда Ф – мера. Сначала рассмотрим случай m(Х) < ¥. Определим множество
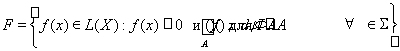
 .
.
Пусть также 
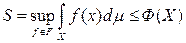 . Тогда найдется такая последовательность {fn(x)}
. Тогда найдется такая последовательность {fn(x)} 
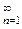 Ì F, что
Ì F, что 
 . Определим при n = 1, 2, … и хÎХ функцию gn(x) =
. Определим при n = 1, 2, … и хÎХ функцию gn(x) = 
 . Тогда по следствию 2 леммы 4.1 gn(x) измерима на X, а поскольку
. Тогда по следствию 2 леммы 4.1 gn(x) измерима на X, а поскольку 
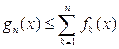 , то и интегрируема при всех п. Проверим, что gn(x)Î F. Неотрицательность этой функции очевидна. Далее, в силу определения функции gn(x) ее можно представить в виде
, то и интегрируема при всех п. Проверим, что gn(x)Î F. Неотрицательность этой функции очевидна. Далее, в силу определения функции gn(x) ее можно представить в виде
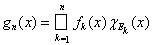
 , где X =
, где X = 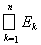
 .
.
Отсюда для любого А ÎS имеем
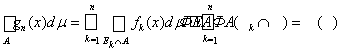
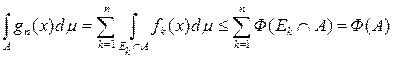 ,
,
т. е. действительно gn(x)Î F. Заметим, что функции {gn(x)} 
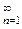 образуют неубывающую на X последовательность. Определим функцию f(x) =
образуют неубывающую на X последовательность. Определим функцию f(x) = 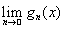
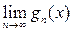 . Поскольку при п = 1, 2,...
. Поскольку при п = 1, 2,... 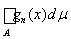
 £ S, то по теореме 13 о монотонной сходимости функция f(x) интегрируема и конечна почти всюду на X. Так как
£ S, то по теореме 13 о монотонной сходимости функция f(x) интегрируема и конечна почти всюду на X. Так как 
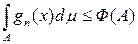 , то
, то 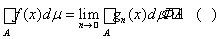
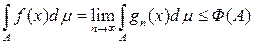 и функция f(x)Î F. Кроме того,
и функция f(x)Î F. Кроме того,

 ,
,
откуда 
 .
.
Теперь рассмотрим заряд l(А) = Ф(А) – 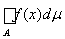
 для любого А ÎS. Этот заряд, очевидно, неотрицателен (т. е. является s-аддитивной мерой) и абсолютно непрерывен относительно меры m. Предположим, что заряд l не равен тождественно нулю. Тогда по лемме 7 найдутся такое n и такое множество В ÎS, что m(В) > 0 и для любого измеримого А Ì В имеем
для любого А ÎS. Этот заряд, очевидно, неотрицателен (т. е. является s-аддитивной мерой) и абсолютно непрерывен относительно меры m. Предположим, что заряд l не равен тождественно нулю. Тогда по лемме 7 найдутся такое n и такое множество В ÎS, что m(В) > 0 и для любого измеримого А Ì В имеем 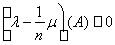
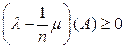 , т. е.
, т. е. 
 . Определим функцию h(x) =
. Определим функцию h(x) = 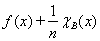
 при x ÎX. Тогда для любого АÎS имеем
при x ÎX. Тогда для любого АÎS имеем


Поэтому h(x) ÎF, в то время, как
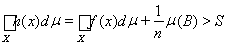

Полученное противоречие показывает, что l = 0 на S, и для случая конечного измеримого пространства доказательство существования завершено.
Пусть теперь X = 
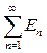 , где m(En) < ¥ при n = 1, 2, … Согласно уже рассмотренному случаю, для каждого n найдется такая интегрируемая на En функция fn(x), что для любого множества А ÎSÇ En = Sn
, где m(En) < ¥ при n = 1, 2, … Согласно уже рассмотренному случаю, для каждого n найдется такая интегрируемая на En функция fn(x), что для любого множества А ÎSÇ En = Sn

 . (4)
. (4)
Заметим, что все функции fn(x) неотрицательны на области своего определения. Продолжим их нулем на все множество X и положим 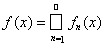
 . Тогда
. Тогда
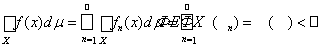
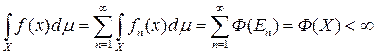 ,
,
откуда следует интегрируемость на Х функции f(x). Нужное нам равенство сразу вытекает из равенств (4) и счетной аддитивности заряда..
Проверим единственность с точностью до почти всюду построенной функции. Если для любого А ÎS
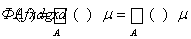
 ,
,
то, обозначая X1 = {xÎX: f(x) > g(x)} и Х2 = {х Î X: f(x) < g(х)}, получим, что

 .
.
Последнее равенство возможно, только если m(Х1) = 0. Аналогично, m(Х2) = 0, и теорема Радона—Никодима полностью доказана.
Исследование, описанное в статье про 6. Заряды. Теорема Радона—Никодима, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 6. Заряды. Теорема Радона—Никодима и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ
Комментарии
Оставить комментарий
Функциональный анализ
Термины: Функциональный анализ