8. Принцип сжимающих отображений и его применение кратко

Привет, Вы узнаете о том , что такое 8. Принцип сжимающих отображений и его применение, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 8. Принцип сжимающих отображений и его применение , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Определение 14. Отображение А метрического пространства X в себя называется сжимающим, если d(Ax, Ay) £ ad(x, y), где 0<a<1.

Теорема 14 (Принцип сжимающих отображений). Если А: X®X сжимающее отображение в полном метрическом пространстве (X, d), то $ единственная точка уÎХ: Ay = y (неподвижная точка).

Доказательство. Для произвольного x1ÎX определим x2 = Ax1, x3 = Ax2, ... xk = Axk-1. Получим последовательность {xk}, для которой d(x3, x2) = d(Ax2, Ax1) £ ad(x2, x1). По такой же схеме выводим общую формулу: d(xn+1 , xn) = d(Axn, Axn-1) £ ad(xn, xn-1) £ ... £ an-1 d(x2, x1). По неравенству треугольника и выведенной формуле получаем

d(xn+p, xn) £ d(xn+p, xn+p-1) +...+ d(xn+1, xn) £ (an+p-2 + an+p-3 +...+ an-1) d(x2, x1) = an-1(1 – ap)d(x2, x1)/(1 – a) £ an-1d(x2, x1)/(1 – a)

(внутреннее равенство – сумма геометрической прогрессии).

В силу неравенства 0<a<1 и неравенства d(xn+p, xn) £ an-1d(x2, x1)/(1 - a) для "e>0 $ N: d(xn+p, xn) < e, n ³ N и любого натурального р. Таким образом, последовательность {xn} является фундаментальной, а следовательно в силу полноты пространства xn ® x0 ÎХ

Теперь докажем, что Аx0 = x0. Имеем d(Ax0, x0) £ d(Ax0, xn) + d(xn, x0) < d(Ax0, Axn-1) + e £ ad(x0, xn-1) + e < 2e (a<1) при достаточно больших n. В силу произвольности e>0 из этого неравенства вытекает, что d(Ax0, x0) = 0. Из аксиом метрики вытекает нужное нам равенство.

Докажем единственность неподвижной точки. Пусть y0ÎX: Ay0 = y0 и y0 ¹ x0. Тогда d(x0, y0) = d(Ax0, Ay0) £ ad(x0, y0) < d(x0, y0) и мы получили противоречие.

Метод отыскания решения уравнения, предложенный в теореме о сжимающих отображениях, называется методом итераций.

Принцип сжимающих отображений имеет многочисленные приложения при доказательствах существования решения и его отыскания. Мы приведем лишь три достаточно важных применения.

1. Задача Коши: Найти решение дифференциального уравнения y¢ = f(x, y) с начальным условием y(x0) = y0.

На функцию f (х, у) наложим следующие условия: f(х, у) определена и непрерывна в некоторой открытой области G, которой принадлежит точка (х0, у0), и удовлетворяет в этой области условию Липшица по у, т.е.

|f(x, y1) - f(x, y2)| £ M|y1 -y2|.

Теорема 15 (Пикара). В приведенных выше условиях существует такое d > 0, что поставленная задача Коши на отрезке |x - x0| £ d имеет единственное решение у = j(х).

Доказательство. Поставленная задача Коши очевидно эквивалентна следующему интегральному уравнению

j(х) = у0 +

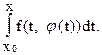
В силу непрерывности функции f(х, у) имеем |f(x, y)| £ K в некоторой замкнутой ограниченной области D Ì G, для которой точка (х0, у0) является внутренней точкой. Выберем d > 0 так, чтобы выполнялись условия:

1) (х, у) Î D, если |х - х0| £ d, |y - y0| £ Kd;

2) Md < 1.

Достаточно очевидно, что эти условия можно удовлетворить. Об этом говорит сайт https://intellect.icu . Рассмотрим множество Х – непрерывных функций j(х), определенных на отрезке |x - x0| £ d и таких, что |j(x) - y0| £ Kd с метрикой d(j1, j2) = max |j1(x) - j2(x)|, где максимум ищется на отрезке [x0 - d, x0 + d]. Несложно видеть, что Х является замкнутым множеством в пространстве С[x0 - d, x0 + d] и следовательно является полным метрическим пространством. Рассмотрим на этом пространстве Х отображение y = Аj, определяемое равенством

y(х) = у0 +

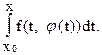
Это отображение переводит пространство Х в себя и является сжатым. Действительно, если jÎХ, |x - x0| £ d, то |y(x) - y0| = 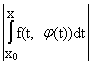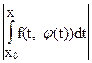£ Kd. Последнее означает, что y(х) = (Аj)(х) ÎХ. Далее, по условию Липшица,

|y1(x) - y2(x)| £ 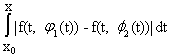£ Md 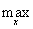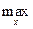|j1(х) - j2(х)|.

В силу предположений Md < 1 и оператор А является сжимающим. Тогда по принципу сжимающих отображений уравнение y(х) = (Аj)(х), а с ним и исходная задача Коши, имеет единственное решение в пространстве Х.

2. Решение систем линейных алгебраических уравнений методом итераций. Рассмотрим n - мерное пространство Rn. Если 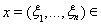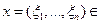Rn, 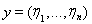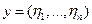Î Rn, то положим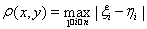 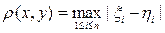. Нетрудно видеть, что определенное так метрическое пространство Rn будет полным. Рассмотрим в этом пространстве отображение Ax = y, заданное с помощью равенств

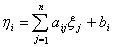
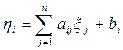, i=1, … , n.

Тогда получаем

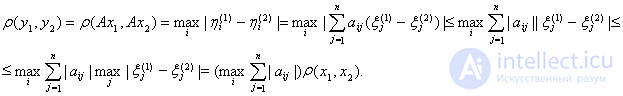
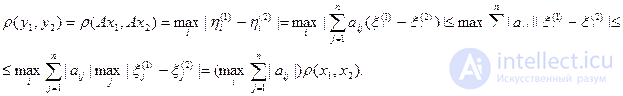Если теперь предположить, что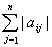 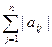<1 для всех i, то мы окажемся в условиях применимости принципа сжатых отображений и, следовательно, отображение будет иметь единственную неподвижную точку. Таким образом, мы получили теорему.

Теорема 16. Если матрица 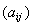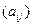такова, что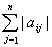 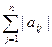<1 для всех i, то система уравнений

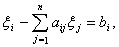
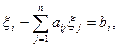i=1, 2, … , n,

имеет единственное решение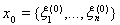

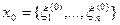
Это решение можно получить методом итераций, исходя из произвольного вектора .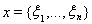

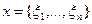Условие теоремы 16 есть достаточное условие сходимости метода итераций для рассматриваемой системы. Если в Rn ввести другую метрику, то получим другое условие сходимости. Пусть, например, 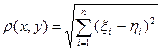. При такой метрике

Поэтому условием сходимости метода итераций будет на этот раз неравенство

.

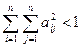Нетрудно видеть, что полученные здесь условия существования и единственности решений для систем линейных уравнений, могут быть распространены достаточно легко на случай бесконечных систем линейных уравнений в соответствующих метрических пространствах.

3. Интегральное уравнение Фредгольма. Применим теперь принцип сжимающих отображений для разрешимости так называемого неоднородного линейного интегрального уравнения Фредгольма второго рода:

f(x) = l 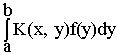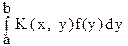+ j(x).

Здесь К(х, у) - называется ядром интегрального оператора, j(x) - заданная функция, l - произвольный параметр, f(х) - искомая функция.

Предположим, что К(х, у) и j(x) - непрерывные функции при a £ x £ b, a £ y £ b. Тогда в силу теоремы Кантора |K(x, y)| £ M. Рассмотрим отображение Аf в метрическом пространстве C[a, b], задаваемое равенством:

(Af)(x) = l 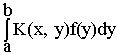+ j(x).

Следующие неравенства вполне очевидны:

d(Af1, Af2) = 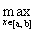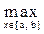|(Af1)(x) - (Af2)(x)| £ |l|M(b - a)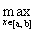 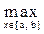|f1(x) – f2(x)|.

Следовательно, при |l| <1/M(b - a) отображение А является сжимающим в пространстве C[a, b]. В силу принципа сжимающих отображений заключаем, что интегральное уравнение Фредгольма при |l| <1/M(b - a) имеет единственное решение, которое можно получить методом итераций по формуле:

fn(x) = l + j(x).

В этой формуле в качестве начального приближения f0(х) можно взять нулевую функцию.

Исследование, описанное в статье про 8. Принцип сжимающих отображений и его применение, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 8. Принцип сжимающих отображений и его применение и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ