3. Сходимость по мере и ее свойства кратко

Привет, Вы узнаете о том , что такое 3. Сходимость по мере и ее свойства, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 3. Сходимость по мере и ее свойства , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Предположим, что {fn(x)} 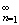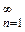и f(x) – измеримые и ко­нечные на измеримом пространстве (X, S, m) функции.

Определение 5. Говорят, что последовательность fn(x) Þ f(x) на X при п ® ¥ (сходится по мере на X), если для любого e > 0 предел

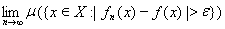
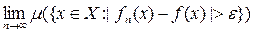= 0.

Отметим, что в отличии от сходимости почти всюду, для которой измеримость предельной функции устанавливается, в определении сходимости по мере сразу предполагается измеримость функции f(x). Поскольку определение сходимости по мере существенно отличается от определений поточечной и равномерной сходимо­сти, установим некоторые свойства этой сходимости.

Теорема 4. Предел последовательности функций, сходящихся по мере, единственен с точностью до эквива­лентности.

Доказательство. Предположим, что последователь­ность fn(x) Þ f(x) и fn(x) Þ g(x) при п ® ¥. Тогда для лю­бого e > О и для любого n имеем

{x Î X: |f(x) - g(x)| > e} Ì {х Î X: |fn(х) - f(х)| > e/2} È {x Î X: |fn(x) - g(х)| > e/2},

откуда ясно, что m({х Î Х: |f(x) - g(х)| > 0}) = 0, т. e. f(x) = g(x) почти всюду.

Теорема 5. Пусть fn(x) Þ f(x) и gn(x) Þ g(x) при п ® ¥. Тогда fn(x) + gn(x) Þ f(x) + g(x) при п ® ¥.

Доказательство. Утверждение теоремы сразу выте­кает из верного для любого e > 0 и для любого n включения

{х Î X: |( fn(x) + gn(x)) - (f(x) + g(х))| > e} Ì

Ì {х Î X: | fn(x) – f(x)| > e/2}È{х Î X: |gn(x) – g(x)| > e/2}.

Теорема 6. Об этом говорит сайт https://intellect.icu . Если m(Х) < ¥, открытое множест­во G Ì R1, функция g(х) непрерывна на множестве G, а по­следовательность fn(x) Þ f(x) при n ® ¥, причем все функ­ции fn(x) и функция f(x) отображают множество X в G, то g(fn(x)) Þ g(f(x)) при n ® ¥.

Доказательство. Так как любой интервал (a, b) на числовой прямой является счетным объединением отрезков [a + 1/n, b – 1/n], то из те­оремы 1.3 вытекает, что справедливо представление 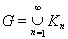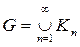, где все множества Кп компактны в R1, т. е. замкнуты и огра­ничены, и K1 Ì К2 Ì ... Рассмотрим прообразы Еп = f -1(Kn) при п = 1, 2,... При этом E1 Ì E2 Ì... и .

Пусть заданы e > 0 и d > 0. По теореме о непрерывности меры можно подобрать r так, что­бы

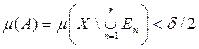
Пусть r > 0 – расстояние от компакта К= 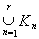до замкнутого множества F = R1 \ G. Определим компакт K0 = {y ÎR1: minxÎK|x - y| £ r/2} Ì G.

Тогда функция g(х) равномерно непрерывна на К0, и, следова­тельно, существует такое s > 0, что при х, у Î К0 и |х – у| < s имеем |g(х) - g(у)| < e.

Выберем N таким образом, чтобы при п > N выполнялось неравенство

m(Bn) = m({x Î X: | fn(x) - f(x)| ³ min(r/2, s)}) < d/2.

Теперь m(АÈВп) < d, а если х Î X\( АÈВп), то f(х) Î К Ì К0, fn(х) Î К0 и | fn(x) - f(x)| < s, откуда | g(fn(x)) - g(f(x))| < e. Теорема доказана.

Следствие 1. Если m(Х) < ¥ и последователь­ность fn(x) сходится по мере к f(x) при n ® ¥, то fn2(x) Þ f 2(x) при n ® ¥. Если же, вдобавок, функции f(x) и fn(x) при n = 1, 2,... не обращаются в нуль на X, то 1/fn(x) Þ 1/ f(x) при n ® ¥.

Замечание. Как показывает пример последова­тельности fn(x) = х + 1/n на прямой R1, условие конечности меры X существенно для справедливости следствия.

Следствие 2. Если m(X) < ¥, последователь­ность fn(x) Þ f(x) и gn(x) Þ g(x) при п ® ¥, то fn(x)gn(x) Þ f(x)g(x) при п ® ¥.

Доказательство. Утверждение сразу вытекает из те­оремы и его первого следствия и следующих равенств:

(fn(x) + gn(x))2 = fn2(x) + 2 fn(x) gn(x) + gn2(x), (f(x) + g(x))2 = f 2(x) + 2f(x)g(x) + g2(x).

.

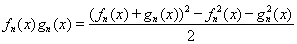
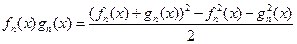Следствие 3. Если m(X) < ¥, последователь­ность fn(x) Þ f(x) и gn(x) Þ g(x) при п ® ¥, причем функции g(х) и gп(х) при n = 1,2,... не обращаются в нуль на X, то fn(x)/gn(x) Þ f(x)/g(x) при п ® ¥.

Исследование, описанное в статье про 3. Сходимость по мере и ее свойства, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 3. Сходимость по мере и ее свойства и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ