3. Принцип равномерной ограниченности и теорема Банаха-Штейнгауза. Полнота пространства операторов относительно поточечной сходимости кратко

Привет, Вы узнаете о том , что такое 3. Принцип равномерной ограниченности и теорема Банаха-Штейнгауза. Полнота пространства операторов относительно поточечной сходимости, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 3. Принцип равномерной ограниченности и теорема Банаха-Штейнгауза. Полнота пространства операторов относительно поточечной сходимости , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Теорема 3 (принцип равномерной ограниченности Банаха-Штейнгаузана). Если последовательность линейных ограниченных операторов 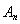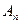ÎL(X, Y) ограничена в каждой точке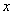 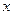банахова пространства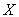 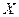, то последовательность норм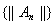 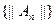этих операторов ограничена.

Доказательство. Для произвольного n рассмотрим множества

Tn = {xÎX: }.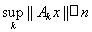

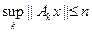В силу непрерывности операторов Аk множества Tn замкнуты: если xiÎTn и xi ® x, то n ³ ||Akxi|| ® ||Akx|| £ n. Более того, в силу условий теоремы Х = ÈnTn. Тогда, в силу теоремы Бэра хотя бы одно из Tn не является нигде не плотным множеством. Последнее означает, что существует шар пространства Х, лежащий полностью в Tn: S[y, r] Ì Tn. Последнее означает, что для любого k и люого хÎ S[y, r] выполняется неравенство ||Akx|| £ n. Тогда в силу леммы 3 ||Ak|| £ 2n/r для любого k. Теорема доказана.

Следствие 1. Если для последовательности линейных ограниченных операторов 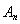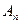ÎL(X, Y) последовательность Аnx фундаментальна в каждой точке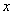 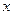банахова пространства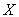 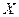, то последовательность норм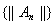 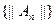этих операторов ограничена.

Доказательство. В силу фундаментальности последовательности Аnx в каждой точке 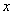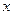банахова пространства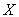 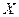, последовательность ||Anx|| ограничена при каждом фиксированном х. Утверждение теперь легко следует из теоремы 3.

Помимо равномерной сходимости в пространстве операторов можно рассматривать еще поточечную сходимость: 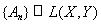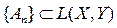сходится поточечно к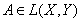 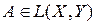, если для любого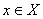

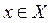
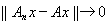
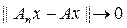при .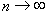

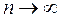Ясно, что из равномерной сходимости следует поточечная. Обратное не верно, как показывает следующий пример.

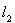
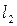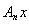
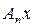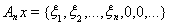
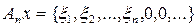Пример 16. В пространстве рассмотрим последовательность операторов , где для . Об этом говорит сайт https://intellect.icu . Так как для любого

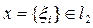
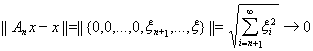
при 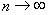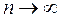, то последовательность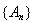 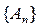поточечно сходится к единичному оператору I, переводящему всякий элемент из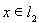 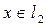в тот же самый элемент. Однако равномерная сходимость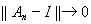 не имеет места, потому что для любого n при

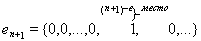
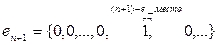
имеем

,

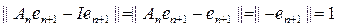и потому для всех n

.

Следствие 2 (теорема Банаха-Штейнгаузана). Для того чтобы последовательность операторов {Аn} Ì L(X, Y), где Х и Y – банаховы пространства, точечно сходилась к оператору A0, необ­ходимо и достаточно, чтобы

1) последовательность {||Аn||} была ограничена;

2) Аnх ® А0х для любого х из некоторого множества E, линейные комбинации элементов которого всюду плотны в Х.

Необходимость первого условия есть не что иное, как следствие из теоремы 3, необходи­мость второго условия очевидна. Требуется доказать лишь достаточность этих условий.

Пусть

М = ,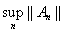

и пусть L(Е) – линейная оболочка множества Е. В силу линейности операторов Аn и А0 и второго условия Аnх ® А0х для любого xÎL(E).

Возьмем теперь элемент y пространства X, не принад­лежащий L(E). Для заданного e > 0 найдется элемент xÎL(E) такой, что ||x – y|| < e/4M. Имеем

||Any – A0y|| £ ||Any – Anx|| + ||Anx – Anx|| + ||A0x – A0y|| £

£ ||Anx – Anx|| +(||An|| + ||A0||)||x – y|| £ ||Anx – Anx|| + e/2.

В силу того, что Аnх ® А0х, найдется номер n0 такой, что ||Anx – Anx|| < e/2 для n > n0. Поэтому для n > n0 имеем ||Any – A0y|| < e и теорема доказана.

Имеет место также следующая

Теорема 4. Если пространства X и Y полные, то пространство 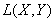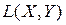также полно в смысле точечной сходимости.

Доказательство. Так как для каждого x последовательность 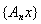фундаментальна и Y полно, то для каждого x существует 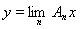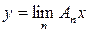и мы получаем операт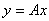ор , определенный на X, с областью значений в Y. Как и в теореме 1, убеждаемся, что A – линейный оператор.

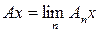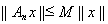
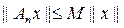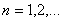
Возвращаясь к оператору из неравенства , 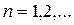вытекающего из теоремы Банаха-Штейнгауза, в пределе при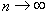 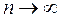получаем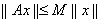 , т. е. ограниченность оператора A.

Итак, существует предел любой точечно фундаментальной последовательности линейных ограниченных операторов, который также является линейным ограниченным оператором, т. е. пространство операторов полно в смысле точечной сходимости. Теорема доказана.

Рассмотрим применение теоремы Банаха-Штейнгауза к доказательству сходимости метода механических квадратур. Для приближенного вычисления интеграла 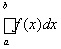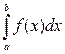применяем формулу

,

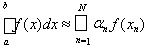
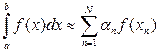где an – коэффициенты формулы, xn – узлы. Метод называется заданным, если фиксирована последовательность формул

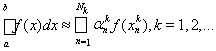
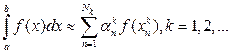(k – индекс).

Метод называется сходящимся, если

.

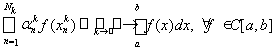
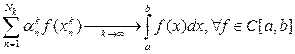Теорема 5. Метод механических квадратур, заданный последовательностями 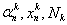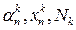сходится тогда и только тогда, когда

1) ;

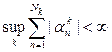2) " n ³ 0 метод сходится при f(x) = xn.

Необходимость практически очевидна, т. к. необходимо проверить лишь 1) условие. Но для его проверки достаточно взять кусочно-линейные непрерывные функции fk(x), которые в узлах принимают значения 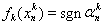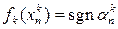(если a или b не является узлом полагаем значение функции в этой точке равной 0). Такие функции заведомо существуют и в силу сходимости и ограниченности 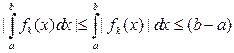первое условие теоремы выполнено.

Достаточность. Рассмотрим последовательность операторов

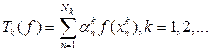
Нетрудно видеть, что это линейные операторы из пространства C[a, b] в пространство R. В силу оценки

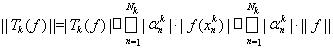
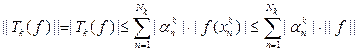
следует, что 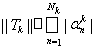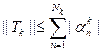. Если взять функции fk(x), построенные при доказательстве необходимости, то нетрудно видеть, что ||fk|| = 1 и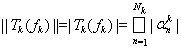 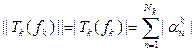. Следовательно .

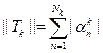Таким образом, последовательность ||Tk|| по условиям теоремы ограничена по норме и поточечно сходится на множестве {xn}, линейная оболочка которого по теореме Вейерштрасса (теорема 2.7) всюду плотна в C[a, b]. По следствию 2 теоремы 3 это эквивалентно поточечной сходимости метода.

Исследование, описанное в статье про 3. Принцип равномерной ограниченности и теорема Банаха-Штейнгауза. Полнота пространства операторов относительно поточечной сходимости, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 3. Принцип равномерной ограниченности и теорема Банаха-Штейнгауза. Полнота пространства операторов относительно поточечной сходимости и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ