Лекция
Привет, Вы узнаете о том , что такое 2. Пространство линейных непрерывных операторов и его полнота относительно равномерной сходимости операторов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 2. Пространство линейных непрерывных операторов и его полнота относительно равномерной сходимости операторов , настоятельно рекомендую прочитать все из категории Функциональный анализ.
Зафиксируем два линейных нормированных пространства 
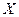 и
и 
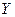 и будем рассматривать всевозможные линейные непрерывные операторы А, В, … действующие из Х в Y. Определим сумму операторов и произведение операторов на число следующим образом: (А + В)х = Ах +Вх, (lА)х = lАх. Это будут снова операторы, действующие из Х в Y, и легко видеть, что все необходимые свойства операций сложения и умножения на число имеют место. В частности, нулевым оператором будет оператор, определяемый равенством 0х = 0 для любого
и будем рассматривать всевозможные линейные непрерывные операторы А, В, … действующие из Х в Y. Определим сумму операторов и произведение операторов на число следующим образом: (А + В)х = Ах +Вх, (lА)х = lАх. Это будут снова операторы, действующие из Х в Y, и легко видеть, что все необходимые свойства операций сложения и умножения на число имеют место. В частности, нулевым оператором будет оператор, определяемый равенством 0х = 0 для любого 
 . Таким образом, совокупность всех операторов, действующих из Х в Y, есть линейное пространство. Более того, эта совокупность будет линейным нормированным пространством. В самом деле, для каждого оператора А определена норма этого оператора
. Таким образом, совокупность всех операторов, действующих из Х в Y, есть линейное пространство. Более того, эта совокупность будет линейным нормированным пространством. В самом деле, для каждого оператора А определена норма этого оператора 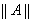
 , являющаяся неотрицательным числом, и остается проверить лишь выполнение аксиом нормы.
, являющаяся неотрицательным числом, и остается проверить лишь выполнение аксиом нормы.
1. Если А = 0, то 
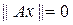 для любого
для любого 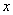
 и потому
и потому 
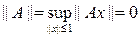 .
.
Пусть, наоборот, 
 . Тогда для любого
. Тогда для любого 


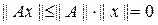 , т. е. Ах = 0 для любого
, т. е. Ах = 0 для любого 
 и
и 
 . Первая аксиома нормы выполняется.
. Первая аксиома нормы выполняется.
2. 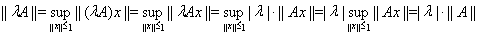
 и вторая аксиома нормы тоже выполняется.
и вторая аксиома нормы тоже выполняется.
3. Подобным же образом проверяется выполнение третьей аксиомы нормы:

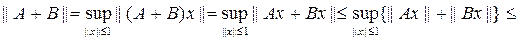


Итак, совокупность всех линейных непрерывных операторов, действующих из X в Y, есть линейное нормированное пространство. Об этом говорит сайт https://intellect.icu . Это пространство мы будем обозначать символом 
 .
.
В частности, когда Y = R – множество вещественных (комплексных) чисел, это пространство называется пространством линейных непрерывных функционалов, определенных на X, или сопряженным с X пространством, и обозначается X*.
Теорема 2. Если Y – полное пространство, то 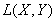
 – пространство линейных ограниченных операторов будет также полным пространством и, следовательно, банаховым пространством.
– пространство линейных ограниченных операторов будет также полным пространством и, следовательно, банаховым пространством.
Доказательство. Пусть 
 и
и 
 при
при 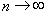
 ,
, 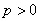
 . Из обратного неравенства треугольника следует
. Из обратного неравенства треугольника следует 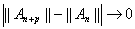
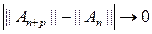 , т. е.
, т. е. 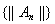
 есть сходящаяся и потому ограниченная числовая последовательность. Положим
есть сходящаяся и потому ограниченная числовая последовательность. Положим 
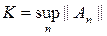 .
.
Возьмем любой элемент 
 и рассмотрим последовательность
и рассмотрим последовательность 
 . Эта последовательность фундаментальна, потому что
. Эта последовательность фундаментальна, потому что


при 
 ,
, 
 . Так как Y – полное пространство, то существует элемент
. Так как Y – полное пространство, то существует элемент 
 , являющийся пределом этой последовательности:
, являющийся пределом этой последовательности: 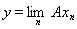
 . Таким образом, каждому
. Таким образом, каждому 
 ставится в соответствие один определенный
ставится в соответствие один определенный 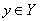
 , и мы приходим к оператору
, и мы приходим к оператору 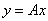
 , действующему из X в Y. Этот оператор линейный:
, действующему из X в Y. Этот оператор линейный:
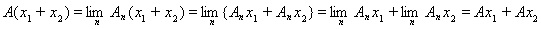
 ,
,

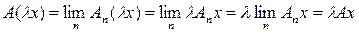 .
.
Этот оператор также ограничен:

 .
.
Следовательно, A – линейный непрерывный оператор.
Покажем, что 
 в смысле сходимости по норме в пространстве
в смысле сходимости по норме в пространстве 
 . Из неравенства
. Из неравенства 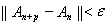
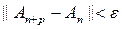 ,
, 
 ,
, 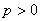
 , будет следовать
, будет следовать

 (7)
(7)
при 
 ,
, 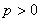
 и для любого
и для любого 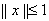
 . Пусть
. Пусть 
 . Тогда (7) в пределе дает
. Тогда (7) в пределе дает 
 при
при 
 и так как это верно для любого x из единичного шара
и так как это верно для любого x из единичного шара 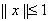
 , то
, то


при 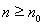
 , что и требовалось доказать.
, что и требовалось доказать.
Следствие. Пространство X*, сопряженное с линейным нормированным пространством X, есть банахово пространство.
Рассмотренную только что сходимость по норме в пространстве операторов называют также равномерной сходимостью последовательности операторов, потому что в этом случае 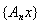
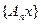 сходится к
сходится к 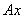
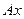 равномерно на любом шаре
равномерно на любом шаре 
 , как это следует из неравенства
, как это следует из неравенства

 .
.
Исследование, описанное в статье про 2. Пространство линейных непрерывных операторов и его полнота относительно равномерной сходимости операторов, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 2. Пространство линейных непрерывных операторов и его полнота относительно равномерной сходимости операторов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ
Из статьи мы узнали кратко, но содержательно про
Комментарии
Оставить комментарий
Функциональный анализ
Термины: Функциональный анализ