7. Сепарабельные топологические пространства кратко

Привет, Вы узнаете о том , что такое 7. Сепарабельные топологические пространства, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 7. Сепарабельные топологические пространства , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Определение 16. Если топологическое пространство X имеет не более чем счетное подмножество А, замыкание которого совпадает с Х, то оно называется сепарабельным. В противном случае пространство называется несепарабельным.

Для метрического пространства (Х, d) это означает, что существует последовательность x1, x2,... элементов из Х такая, что для "xÎX,"e>0 $ n(e, x): d(xn, x) < e.

Пример 20. s - сепарабельное пространство. Действительно, рассмотрим jr подмножество из s последовательностей, координаты которых являются рациональными числами и начиная с некоторого номера все координаты равны 0. Если обозначить jr(n) – множество последовательностей, у которых первые n координат рациональные числа, а последующие координаты 0, то это множество будет счетным, как конечное объединение счетных множеств. Так как jr = 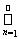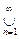jr(n), то оно счетно, как счетное объединение счетных множеств. Об этом говорит сайт https://intellect.icu . С другой стороны, для заранее заданного e>0 найдется номер m такой, что

.

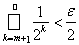
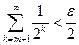Тогда для любой последовательности х = {xn} и любого n найдется такое рациональное число rn, что |rn - xn|< e/2. Обозначим через r последовательность, у которой первые m координат равны rn а последующие равны 0. Тогда r Î jr и

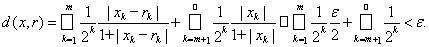
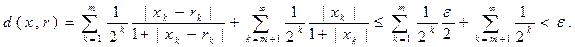
Пример 21. lp, 1£p<¥ - сепарабельно. В этом случае в качестве счетного всюду плотного подмножества можно взять тоже самое множество jr из предыдущего примера. При этом рациональные числа подбираются исходя из неравенств: |rn-xn|< e/2n/p (проверьте самостоятельно нужное неравенство).

Пример 22. m- несепарабельно. Для проверки этого докажем следующее утверждение.

Лемма 1. Если в метрическом пространстве Х $ d>0 и несчетное множество {xa}: d(xa, xb) ³ d, a ¹ b, Х – несепарабельное пространство.

Доказательство. От противного предположим, что Х - сепарабельно. Тогда существует счетное множество {yk} такое, что для e = d/2, 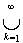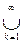Se(yk) = X. Так как {yk} - счетное, {xa} -несчетное, то найдется хотя бы один шар Se(yk), в котором будет более одного элемента из {xa}. Пусть xa, xbÎSe(yk) a ¹ b. Тогда d £ d(xa, xb) £ d(xa,yk) + d(yk, xb) < 2e = d и d < d - получили противоречие.

Для доказательства несепарабельности пространства m достаточно воспользоваться этой леммой. В качестве нужного семейства рассматриваются элементы из m, у которых координаты равны либо 0, либо 1. Тогда расстояние между различными элементами этого семейства равно единице. Используя диагональный метод Кантора можно убедиться, что рассмотренное семейство несчетно.

Отметим без доказательства, что сепарабельность топологического пространства влечет наличие в нем счетной базы. Обратное вообще говоря неверно. Однако в случае метрических пространств, наличие счетной базы топологии влечет сепарабельность.

Исследование, описанное в статье про 7. Сепарабельные топологические пространства, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 7. Сепарабельные топологические пространства и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ