2. Сходимость почти всюду кратко

Привет, Вы узнаете о том , что такое 2. Сходимость почти всюду, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 2. Сходимость почти всюду , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Пусть (X, S, m) – измеримое пространство со счетно-аддитивной полной мерой m и множество Е Î S. Далее мы пишем, что функции f £ g на множестве Е, если выполняется неравенство f(x) £ g(x) при всех х Î Е.

Определение 2. Последовательность функций {fn} на множестве Е сходится к функции f(х) = 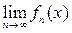, если выполняется равенство f(x) = 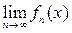при всех х Î Е.

Последовательность функций {fn} сходится монотонно возрастая fn ­ f на Е, если f = 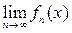, на Е и последовательность не убывает fi £ fi+l, i =1,2,..., на множестве Е. Аналогично определяется монотонная сходимость вида fn ¯ f на множестве Е.

Определение 3. Функция h: Е ® R называется простой, если она имеет конечное множество значений. Пусть h принима­ет значения hj на множествах Hj, j = 1, 2, ...,k. Тогда Hj образуют конечное разбиение множества и имеет место равенство

,

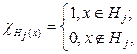
где 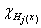- характеристическая функция множества Hj. Непосредственной проверкой убеждаемся, что простая функция h(x) измерима тогда и только тогда, когда все множества Hj измеримы. В приведенном представлении предполагается, что hj различны при различных значениях j. На практике встречаются случаи, когда отслеживать данное условие обременительно, и мы допускаем, что при разных значениях индекса могут быть одни и те же значения функции.

Теорема 2. Для каждой неотрицательной измери­мой функции f на множестве Е Î S найдется такая последовательность простых неотрицательных изме­римых функций hn(х), которая сходится монотонно hn ­ f на множестве Е.

Доказательство. Зададим последовательность простых функций на множестве Е по формуле:

,

где 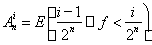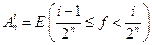и Вп = E(f ³ 2n). Об этом говорит сайт https://intellect.icu . Эти функции неотрицательны и измеримы на множестве Е. Покажем, что последовательность простых функций {hn} является неубывающей. Поскольку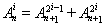 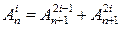, то

.

Далее, так как 0 £ f(x) – hn(x) < 1/2n при всех х Î E(f < 2n), то эта последовательность сходится монотонно к функции f на множестве Е.

Следствие 1. Для каждой неотрицательной ограниченной измери­мой функции f на множестве Е Î S найдется такая последовательность hn(х) простых неотрицательных изме­римых функций, что {hn} сходится монотонно и равномерно на множестве Е к функции f.

Утверждение следствия установлено по существу в ходе доказательства теоремы.

Определение 4. Последовательность функций {fn} сходится почти всюду (п. в.) к функции f на множе­стве Е, если существует такое множество АÎS меры нуль m(А) = 0, что справедливо равенство f(x) = 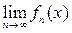при всех х Î Е\A.

Две функции называются эквивалентными f~g, если существует такое множество А Î Е меры нуль m(А) = 0, что f(x) = g(x) при всех х Î Е\А. В силу полноты меры из измеримости функции вытекает измеримость любой эквивалентной функции.

В пространстве S(E) всех измеримых функций на множестве Е эквивалентные функции отождествляются так, что элементами этого пространства, на самом деле, являются классы эквивалентных функций.

Нетрудно проверить, что предел f(x) = 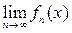почти всю­ду сходящейся последовательности измеримых функций является также измеримой функцией и определяется од­нозначно с точностью до эквивалентности. Действительно, пусть А множество нулевой меры из определения. Тогда последовательность {fncЕ\А} сходится для всех x Î E\A к функции f(x) cЕ\А. В силу следствия 2 из леммы 1 последняя функции является измеримой. Тогда функция f(x) cЕ\А + cА является измеримой на Е, как сумма двух измеримых функций. Причем построенная функция эквивалента f(x), а следовательно, последняя является измеримой функцией.

Лемма 2. Пусть Е = {x ÎX: fn(x) ® f(x) при п ®¥}. Тогда

X\E =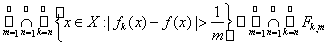

Доказательство. Точка x Î X \ E в том и только в том случае, когда fn(x) не сходится к f(x). Но последнее по определе­нию означает, что для некоторого m0 при любом п ³ 1 найдется такое k > п, что |fk(x) – f(x)| > 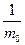. Последнее означает, что х Î 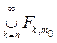для любого n. Следовательно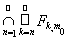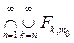, х Î и х Î 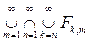. Обратное включение проверяется уже просто.

Теорема 3 (критерий сходимости почти всюду). Пусть m(Х) <¥. Тогда последователь­ность fn(x) ® f(x) почти всюду на X в том и только в том случае, когда для любого e > 0 выполнено равенство

.

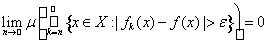
Доказательство. Достаточно установить, что сходи­мость почти всюду эквивалентна тому, что для любого натураль­ного т

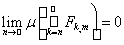
В обозначениях леммы 2 сходимость fn(x) ® f(x) почти всю­ду на X эквивалентна тому, что m(Х \Е) = 0 или . Но это, в свою очередь, равносильно тому, что для любого т выполнено равенство 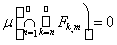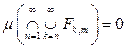. Определим для фиксированного m множества Gn =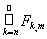 при всех натуральных п. Тогда G1 É G2 É... Для завершения доказательства остается только заметить, что по теореме о непрерывности меры (теорема 3.5)

.

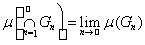
Исследование, описанное в статье про 2. Сходимость почти всюду, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 2. Сходимость почти всюду и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ