3. Теорема Рисса об общем виде линейного функционала для пространства непрерывных функций кратко

Привет, Вы узнаете о том , что такое 3. Теорема Рисса об общем виде линейного функционала для пространства непрерывных функций, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 3. Теорема Рисса об общем виде линейного функционала для пространства непрерывных функций , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Рассмотрим пространство C[a,b] непрерывных вещественных функ­ций на отрезке [a,b], которое имеет чебышевскую норму

.

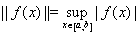
Наша цель описать сопряженное пространство к С[а, b].

Пусть на отрезке [а, b] задана конечная вещественная функция f (x). Разложим отрезок [а, b] на части точками x0 = a < x1 < …< xn = b и составим сумму

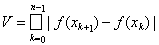
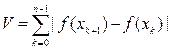
Определение 1. Точная верхняя грань всевозможных сумм V называется полной вариацией функции f (x) на отрезке [а, b] и обозначается 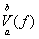. Если полная вариации f (x) конечна, то функция называется функцией ограниченной вариации.

Пусть далее V[а, b] обозначает пространство всех вещественных функ­ций g: [a, b] ® R ограниченной вариации на отрезке [a, b]. В этом пространстве 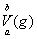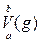– полная вариация функции g является полунормой (см. теорему Хана-Банаха):

Считая две функции f, g Î V[а, b] эквивалентными f ~ g, если их разность f(x) – g(x) = с есть константа, получим нормированное пространство, в котором нормой является полная вариация ||g|| = 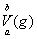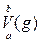функции gÎ V[a, b].

Так как любая непрерывная слева функция g(x) ограниченной вариации определяет заряд (задача 5.24) и справедливо разложение Жордана для зарядов (определение 5.7), то с помощью мер, порождаемых этим разложением можно построить интегралы Лебега, разность которых называется интегралом Лебега-Стильтьеса и обозначается

Теорема 4 (Рисса). Об этом говорит сайт https://intellect.icu . Для любого ограниченного линейного функ­ционала aÎС*[а, b] найдется такая функция ограни­ченной вариации gÎ V[a, b], что функционал представ­ляется в виде интеграла Лебега-Стилтьеса:

и его норма равна вариации ||a|| = 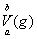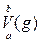функции g.

Доказательство. Пространство непрерывных функций есть замкнутое подпространство в пространстве M[a, b] ограниченных функций на отрезке [a, b].

По следствию из теоремы Хана-Банаха каждый функ­ционал aÎС*[а, b], определенный на подпространстве С[а, b], имеет продолжение на все пространство M[a, b] с сохранением его нормы. Это продолжение мы будем обозначать также через а.

Пусть ut(x) = c[a, t)(x) – характеристическая функция полуинтервала [a, t), если а £ t < 1, и функция иb(х) = 1 на отрезке [a, b]. Покажем, что функция g(t) = a(ut) имеет ограниченную вариацию на [a, b]. Действительно, для данного разбиения t отрезка [a, b], оценим сумму

=

= ,

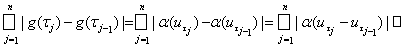
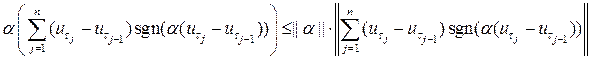где последнее неравенство вытекает из определения нор­мы функционала. Так как функция 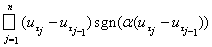на отрезке принимает лишь два значения, либо +1 , либо -1, то = 1 и мы получили неравенство 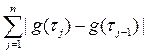£ ||a||. Отсюда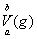 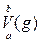£ ||a|| и, следовательно, величина вариа­ции функции g будет конечной на отрезке [a, b].

Возьмем теперь произвольную непрерывную функцию f Î С[a, b] и построим ступенчатую функцию

,

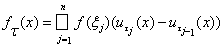
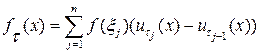где xj Î[tj – 1, tj]. Пусть dt = maх(tj - tj - 1) – диаметр разбиения. Тогда для любой последовательности разбиений с dt ® 0 после­довательность функций ft сходится равномерно к f на отрезке [a, b] и в силу непрерывности функционала a(f ) получим, что предел 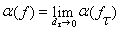равен интегралу Стилтьеса

.

Таким образом, каждый ограниченный функционал a из сопряженного пространства C*[a,b] представляется ин­тегралом Стилтьеса относительно функции g(t) = a(ut) ограниченной вариации на отрезке [a, b] и теорема доказана.

Нетрудно показать, что для любой функции ограниченной вариации, выражение из теоремы 3 определяет линейный непрерывный функционал. Можно также установить, что пространство C*[a,b] изометрически изоморфно пространству функций ограниченной вариации, непрерывных слева на интервале (a, b).

Покажем, что пространство С[0, l] не является рефлексивным, т. е. образ ImJ отобра­жения двойственности не совпадаете С**[0, 1].

Для этого мы рассмотрим функционал a(g) = g(+0) – g(0) на пространстве функций gÎ V[0, 1] ограниченной вариации. Поскольку при всех gÎ V[0, 1], |g(+0) – g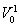(0)| £ (g), h(+0) – h(0) = 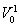(h) = 1, где h(0) = 0 и h(x) = 1, если 0 < x £ 1, тo норма ||a|| = 1. Предположим теперь, что существует непрерывная функция f Î С[0, 1] такая, что

a(g) = g(+0) – g(0) = 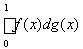, g Î V[0, 1].

В частности, равенство верно для функции g(x) = . Поэтому, подставляя эту функцию, получим

a(g) = 0 =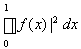

Отсюда следует, что функция равна нулю f = 0, а значит и функционал также равен нулю a = 0. Таким образом, имеет место противоречие с условием ||a|| = 1.

Исследование, описанное в статье про 3. Теорема Рисса об общем виде линейного функционала для пространства непрерывных функций, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 3. Теорема Рисса об общем виде линейного функционала для пространства непрерывных функций и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ