2. Конечномерные пространства. Конечномерность и компактность. Теорема Рисса о локальной компактности. кратко

Привет, Вы узнаете о том , что такое 2. Конечномерные пространства. Конечномерность и компактность. Теорема Рисса о локальной компактности., Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 2. Конечномерные пространства. Конечномерность и компактность. Теорема Рисса о локальной компактности. , настоятельно рекомендую прочитать все из категории Функциональный анализ.

Пусть даны два линейных нормированных пространства Е1 и Е2. Мы будем называть эти пространства изоморфными, если существует взаимнонепрерывное (гомеоморфизм) биективное отображение Е1 на Е2. Имеет место следующая важная теорема:

Теорема 3. Все конечномерные линейные нормированные пространства данного числа измерений n изоморфны евклидову n-мерному пространству Rn и, следовательно, изоморфны друг другу.

Доказательство. Пусть Е есть n – мерное линейное нормированное пространство с нормой ||·|E|| и е1,…,еn - базис этого пространства. Тогда любой элемент однозначно представим в виде

x= ξ1e1+ …+ ξnen.

Поставим элементу 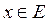в соответствие элемент

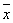
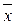= (ξ1, …, ξ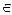n) Rn

Очевидно, что таким образом установленное соответствие между элементами x и 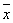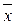является взаимно однозначным. Кроме того, это соответствие есть изоморфизм линейных пространств Е и Rn. Покажем, что оно взаимно непрерывно.

Для любого 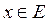имеем

(1)

В частности,

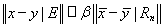
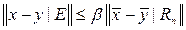, (2)

где β не зависит от x и y.

Установим теперь неравенство противоположного знака. На поверхности S единичного шара 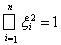пространства Rn (т.е. на компактном замкнутом множестве) рассмотрим функцию

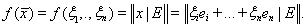
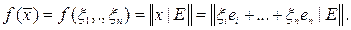
Так как на S все ξi не могут одновременно обращаться в нуль, то в силу линейной независимости е1,…,еn имеем

.

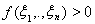
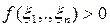Неравенство

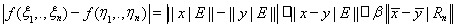
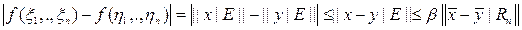
показывает, что 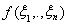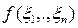- непрерывная функция. По теореме Вейерштрасса эта функция достигает на S своего минимума α. Легко видеть, что α>0. Следовательно, для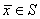

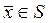
откуда для любого 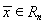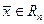имеем

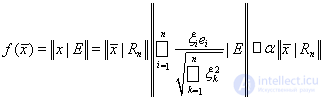
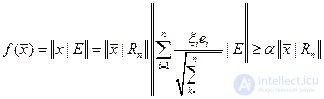(3)

Из (1) и (3) следует взаимная непрерывность отображения E на Rn. Об этом говорит сайт https://intellect.icu . Теорема доказана.

Из гомеоморфизма E и Rn следует, что в конечномерном линейном нормированном пространстве сходимость по норме сводится к покоординатной сходимости и поэтому такое пространство всегда полное.

Для подпространства линейного нормированного пространства имеет место следующее важное предположение, установленное Ф. Риссом:

Теорема 4 (лемма Рисса о почти перпендикуляре). Пусть L – подпространство линейного нормированного пространства Е, несовпадающее с Е. Тогда для любого заданного ε > 0 найдется в Е такой элемент y с нормой, равной единице, что

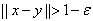
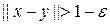для всех x 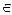L.

Доказательство. Пусть y0 – любой элемент из Е, не принадлежащий L, и

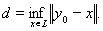
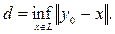
Тогда d > 0, так как иначе y0 был бы предельным элементом для L и, следовательно, в силу замкнутости L, входил бы в L, что невозможно по условию. Далее

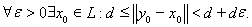
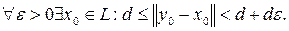
Положим .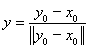

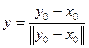Элемент 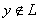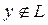(т.к. иначе 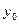входил бы в L) и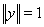 Возьмем любой элемент 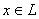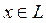. Пусть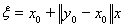 , xÎL. Тогда

,

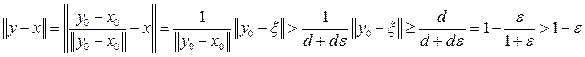что и требовалось доказать.

Известно, что в n-мерном евклидовом пространстве всякое ограниченное множество компактно. Докажем, что компактность ограниченных множеств, есть характеристическое свойство конечномерных линейных нормированных пространств.

Теорема 5 (теорема Рисса о локальной компактности). Для того, чтобы подпространство L линейного нормированного подпространства Е было конечномерным, необходимо и достаточно, чтобы каждое ограниченное множество элементов из L было относительно компактно.

Необходимость. Пусть L n-мерно. Тогда L гомеоморфно n-мерному евклидову пространству Rn. Ограниченное множество 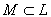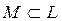взаимно однозначно и взаимно непрерывно преобразуется в ограниченное множество N Ì Rn, и так как N в Rn относительно компактно, то M в L также относительно компактно.

Достаточность. Предположим, что каждое ограниченное множество элементов из L относительно компактно. Возьмем в L произвольный элемент x1, 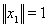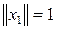. Обозначим через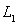 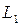подпространство, порожденное элементом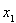 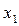. Если L =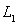 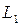, то теорема доказана. Если же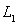 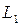не совпадает с L, то по теореме 3. найдется в L элемент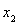 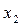такой, что 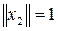и 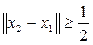. Обозначим через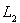 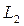подпространство, порождаемое элементам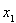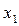и и 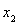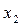. Имеются 2 возможности: либо L =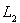 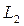и теорема доказана, либо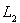 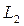не совпадает с L. Тогда по той же теореме найдется элемент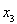 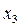такой, что 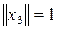и . Продолжим этот процесс. 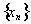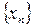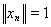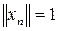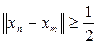Тогда можно сделать 2 предположения: либо для некоторого n подпространство совпадет с L и теорема будет доказана, либо мы построим бесконечную последовательность такую, что и при 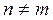для любых n и m,. Но вторая возможность отпадает, т.к. она означала бы существование ограниченного (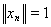 ) множества 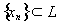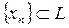, из которого нельзя выделить фундаментальную подпоследовательность (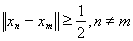 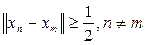), что противоречит условию теоремы.

Исследование, описанное в статье про 2. Конечномерные пространства. Конечномерность и компактность. Теорема Рисса о локальной компактности., подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 2. Конечномерные пространства. Конечномерность и компактность. Теорема Рисса о локальной компактности. и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ