Лекция
Привет, Вы узнаете о том , что такое 5. Примеры обратных операторов. Обратимость операторов вида (I - A) и (A - C)., Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 5. Примеры обратных операторов. Обратимость операторов вида (I - A) и (A - C). , настоятельно рекомендую прочитать все из категории Функциональный анализ.
Рассмотрим теперь множество линейных ограниченных операторов, отображающих линейное нормированное пространство 
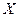 в себя.
в себя.
B пространстве операторов 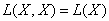
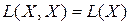 , действующих в банаховом пространстве X можно рассматривать произведение операторов. Именно, если
, действующих в банаховом пространстве X можно рассматривать произведение операторов. Именно, если 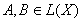
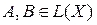 , то АВ есть оператор, определяемый равенством
, то АВ есть оператор, определяемый равенством 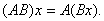
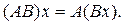
Отличительной особенностью этого произведения является его некоммутативность, потому что, вообще говоря, АВ 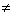
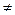 ВА. Чтобы получить пример некоммутирующих операторов, достаточно взять в Rn два оператора, A и В, заданные некоммутирующими матрицами
ВА. Чтобы получить пример некоммутирующих операторов, достаточно взять в Rn два оператора, A и В, заданные некоммутирующими матрицами 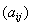
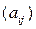 и
и 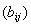
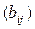 . Так как оператор АВ задается произведением матриц
. Так как оператор АВ задается произведением матриц 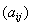
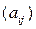 и
и 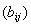
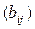 , что легко проверить, то некоммутируемость таких операторов очевидна. Свойством дистрибутивности произведение операторов обладает, так как из определения суммы и произведения операторов следует, что
, что легко проверить, то некоммутируемость таких операторов очевидна. Свойством дистрибутивности произведение операторов обладает, так как из определения суммы и произведения операторов следует, что
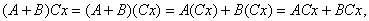
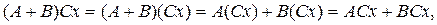
т.е. что 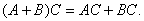
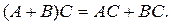
Отметим, что если I – единичный оператор, то 
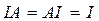 для любого
для любого 

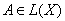
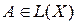 .
.
Нетрудно проверить, что 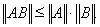
 В самом деле, пусть
В самом деле, пусть 
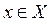 и
и 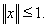
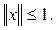 Тогда
Тогда
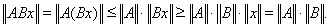
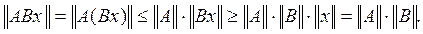
Поэтому

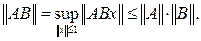
Из доказанного неравенства, в частности, следует, что если 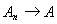
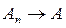 и
и 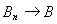
 в смысле равномерной сходимости, то
в смысле равномерной сходимости, то 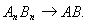
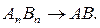
Прежде всего из сходимости последовательности 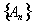
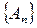 к А следует, что
к А следует, что 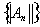
 есть ограниченная числовая последовательность, т. е.
есть ограниченная числовая последовательность, т. е. 
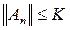 для любого n. Поэтому
для любого n. Поэтому
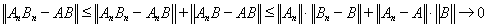
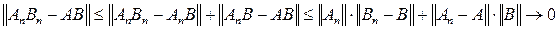
при 
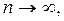 так как в каждом слагаемом справа один множитель ограничен, а другой стремиться к нулю.
так как в каждом слагаемом справа один множитель ограничен, а другой стремиться к нулю.
Частным случаем произведения операторов являются степени оператора

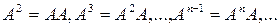
Ясно, что 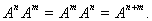
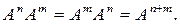
Положим, кроме того, по определению, что 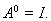
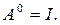
Теорема 7. Об этом говорит сайт https://intellect.icu . Пусть 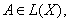
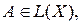 где X – банахово пространство и
где X – банахово пространство и 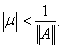
 Тогда оператор
Тогда оператор 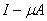
 имеет обратный линейный и ограниченный оператор, причем
имеет обратный линейный и ограниченный оператор, причем
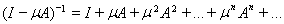
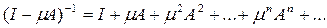
Доказательство. Рассмотрим ряд
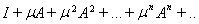
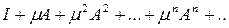 (12)
(12)
и составим частичные суммы этого ряда:
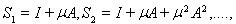
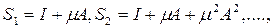

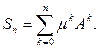
Имеем
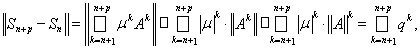
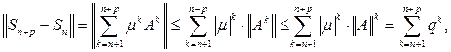
где 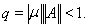
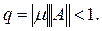 Отсюда следует, что
Отсюда следует, что 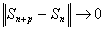
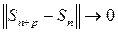 при
при 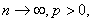
 т.е. последовательность частичных сумм ряда (12) является фундаментальной. В силу полноты пространства операторов существует
т.е. последовательность частичных сумм ряда (12) является фундаментальной. В силу полноты пространства операторов существует 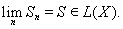
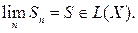
Покажем, что 
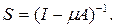 Имеем
Имеем
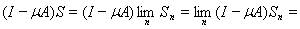
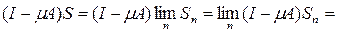
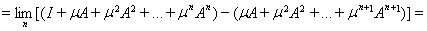
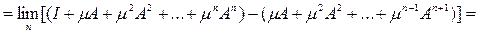
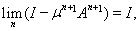
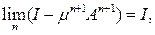
ибо 
 как общий член сходящегося ряда. Аналогично убеждаемся, что
как общий член сходящегося ряда. Аналогично убеждаемся, что 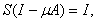
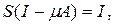 и теорема полностью доказана.
и теорема полностью доказана.
Применим доказанную теорему к интегральным уравнениям.
Пример 19. Пусть 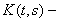
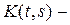 непрерывное на
непрерывное на 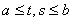
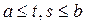 ядро и
ядро и 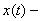
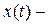 непрерывная на
непрерывная на 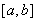
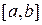 функция. Тогда
функция. Тогда
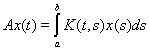
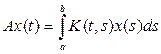
есть линейный оператор, действующий в пространстве 
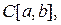 а интегральное уравнение
а интегральное уравнение

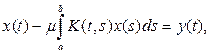 (13)
(13)
называется уравнением Фредгольма второго рода, можно записать в операторной форме 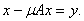
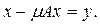
На основании предыдущей теоремы мы получаем, что если 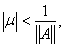
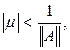 то уравнение (13) имеет единственное решение, которое дается равенством
то уравнение (13) имеет единственное решение, которое дается равенством

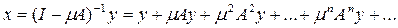
Рассмотрим подробнее это решение и условия, при которых оно существует. Так как 
 то условие
то условие 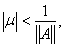
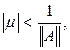 очевидно, выполняется, если
очевидно, выполняется, если 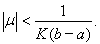
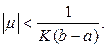 Будем считать, что
Будем считать, что 
 удовлетворяет этому неравенству. Выясним, что представляют в нашем случае степени оператора. Имеем
удовлетворяет этому неравенству. Выясним, что представляют в нашем случае степени оператора. Имеем
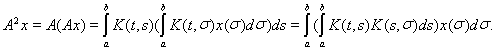

Пусть 
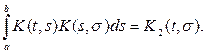 Функция
Функция 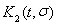
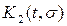 называется второй итерацией ядра
называется второй итерацией ядра 
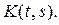
Итак,

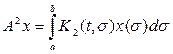
или, меняя обозначение переменной интегрирования,
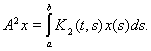
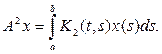
Далее,
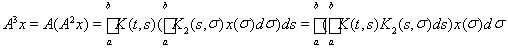
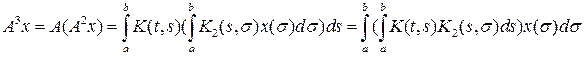
и, снова пологая
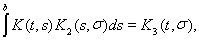
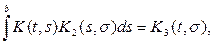
можем написать
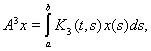
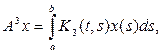
где 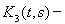
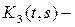 третья итерация ядра
третья итерация ядра 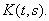
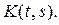 Вообще
Вообще
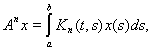

где 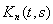
 – n-я итерация ядра
– n-я итерация ядра 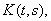
 определяемая формулой
определяемая формулой
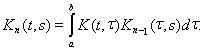

Равенства 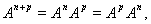
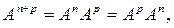 которое мы отмечали выше, дают
которое мы отмечали выше, дают
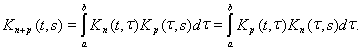
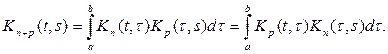
С помощью итерированных ядер решение интегрального уравнения может быть записано так:
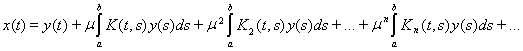
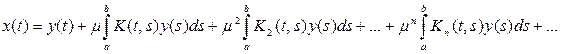 (14)
(14)
Ряд, стоящий в правой части этого равенства, сходится в смысле сходимости в пространстве C[a, b], т.е. равномерно. Преобразуем выражение для решения интегрального уравнения. Рассмотрим формальный ряд
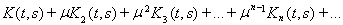
 (15)
(15)
Этот ряд равномерно сходится на 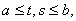
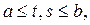 если
если 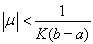
 . В самом деле, прежде всего имеем
. В самом деле, прежде всего имеем

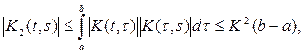
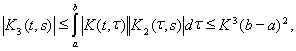
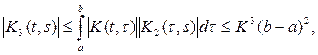
и вообще 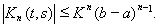

Отсюда 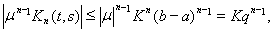
 где
где 
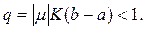 Таким образом, общий член исследуемого функционального ряда не превосходит по абсолютной величине члена сходящегося числового ряда, и требуемая равномерная сходимость доказана. Обозначим сумму этого ряда R(t, s,
Таким образом, общий член исследуемого функционального ряда не превосходит по абсолютной величине члена сходящегося числового ряда, и требуемая равномерная сходимость доказана. Обозначим сумму этого ряда R(t, s, 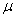
 ). Это - непрерывная функция. Умножая члены ряда (15) на
). Это - непрерывная функция. Умножая члены ряда (15) на 
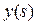 и интегрируя ряд почленно, получим
и интегрируя ряд почленно, получим

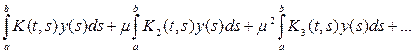


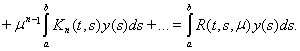
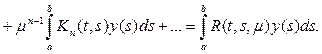
Сравнивая это выражение с выражением (14) для решения интегрального уравнения, можем написать
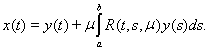
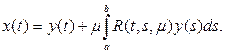 (16)
(16)
Это и есть выражение для обратного оператора 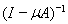
 в компактной форме. Функция R(t, s,
в компактной форме. Функция R(t, s, 
 ) называется разрешающим ядром рассматриваемого уравнения Фредгольма.
) называется разрешающим ядром рассматриваемого уравнения Фредгольма.
Сравните полученное решение с решение в главе 2 п. 2.
Пример. 20. Рассуждениями, аналогичными проведенным выше, легко показать, что если

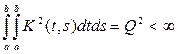
и 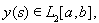
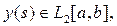 то интегральное уравнение (13) при значениях параметра m, удовлетворяющих неравенству
то интегральное уравнение (13) при значениях параметра m, удовлетворяющих неравенству 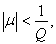
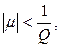 имеет решение, выражаемое формулой (16), где разрешающее ядро R(t, s,
имеет решение, выражаемое формулой (16), где разрешающее ядро R(t, s, 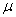
 ), по переменным t и s имеет интегрируемый квадрат, и ряд (15), его изображающий, сходится в среднем.
), по переменным t и s имеет интегрируемый квадрат, и ряд (15), его изображающий, сходится в среднем.
Исследование, описанное в статье про 5. Примеры обратных операторов. Обратимость операторов вида (I - A) и (A - C)., подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 5. Примеры обратных операторов. Обратимость операторов вида (I - A) и (A - C). и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Функциональный анализ
Из статьи мы узнали кратко, но содержательно про
Комментарии
Оставить комментарий
Функциональный анализ
Термины: Функциональный анализ