Понятие Матрицы как математического объекта, операции над матрицами, прменение

Лекция

Привет, Вы узнаете о том , что такое матрица, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое матрица, операции над матрицами, транспонирование , настоятельно рекомендую прочитать все из категории Линейная алгебра и аналитическая геометрия.

матрица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся ее элементы. Количество строк и столбцов задает размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы , в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.

Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.

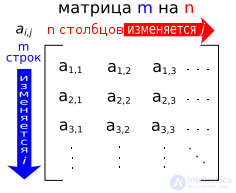
Понятие Матрицы как математического объекта, операции над матрицами, прменение

Структура матрицы

Для матрицы определены следующие алгебраические операции:

сложение матриц, имеющих один и тот же размер[⇨];
умножение матриц подходящего размера (матрицу, имеющую столбцов, можно умножить справа на матрицу, имеющую строк)[⇨];
в том числе умножение на матрицу вектора (по обычному правилу матричного умножения; вектор является в этом смысле частным случаем матрицы)[⇨];
умножение матрицы на элемент основного кольца или поля (то есть скаляр)[⇨].

Относительно сложения матрицы образуют абелеву группу; если же рассматривать еще и умножение на скаляр, то матрицы образуют модуль над соответствующим кольцом (векторное пространство над полем). Множество квадратных матриц замкнуто относительно матричного умножения, поэтому квадратные матрицы одного размера образуют ассоциативное кольцо с единицей относительно матричного сложения и матричного умножения.

Доказано, что каждому линейному оператору, действующему в n-мерном линейном пространстве, можно сопоставить единственную квадратную матрицу порядка n; и обратно — каждой квадратной матрице порядка n может быть сопоставлен единственный линейный оператор, действующий в этом пространстве. Свойства матрицы соответствуют свойствам линейного оператора. В частности, собственные числа матрицы — это собственные числа оператора, отвечающие соответствующим собственным векторам.

То же можно сказать о представлении матрицами билинейных (квадратичных) форм.

В математике рассматривается множество различных типов и видов матриц. Таковы, например, единичная, симметричная, кососимметричная, верхнетреугольная (нижнетреугольная) и т. п. матрицы.

Особое значение в теории матриц занимают всевозможные нормальные формы, то есть канонический вид, к которому можно привести матрицу заменой координат. Наиболее важной (в теоретическом значении) и проработанной является теория жордановых нормальных форм. На практике, однако, используются такие нормальные формы, которые обладают дополнительными свойствами, например, устойчивостью.

История[ | ]

Впервые матрицы упоминались еще в древнем Китае, называясь тогда «волшебным квадратом». Основным применением матриц было решение линейных уравнений . Также волшебные квадраты были известны чуть позднее у арабских математиков, примерно тогда появился принцип сложения матриц. После развития теории определителей в конце 17-го века Габриэль Крамер начал разрабатывать свою теорию в 18-м столетии и опубликовал «правило Крамера» в 1751 году. Примерно в этом же промежутке времени появился «метод Гаусса». Теория матриц начала свое существование в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу. Термин «матрица» ввел Джеймс Сильвестр в 1850 г.

Введение[ | ]

Матрицы естественным образом возникают при решении систем линейных уравнений, а также при рассмотрении линейных преобразований.

Системы линейных уравнений

Рассмотрим систему линейных уравнений вида:

$\begin{cases}a_{11}x_1 + a_{12}x_2 + \ldots + a_{1n}x_n = b_1 \\a_{21}x_1 + a_{22}x_2 + \ldots + a_{2n}x_n = b_2 \\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\a_{m1}x_1 + a_{m2}x_2 + \ldots + a_{mn}x_n = b_m \end{cases}$ .

Эта система состоит из Понятие Матрицы как математического объекта, операции над матрицами, прменение линейных уравнений относительно неизвестных. Она может быть записана в виде следующего матричного уравнения :

Понятие Матрицы как математического объекта, операции над матрицами, прменение ,

где

$A = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} ; \quad x = \begin{pmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{pmatrix} ; \quad b = \begin{pmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{m} \end{pmatrix}$

Матрица Понятие Матрицы как математического объекта, операции над матрицами, прменение — это матрица коэффициентов системы линейных уравнений, вектор-столбец — вектор неизвестных, а вектор-столбец Понятие Матрицы как математического объекта, операции над матрицами, прменение — некоторый заданный вектор.

Для того, чтобы система имела решение (хотя бы одно), необходимо и достаточно, чтобы вектор Понятие Матрицы как математического объекта, операции над матрицами, прменение был линейной комбинацией столбцов , и тогда вектор — это вектор, содержащий коэффициенты разложения вектора Понятие Матрицы как математического объекта, операции над матрицами, прменение по столбцам матрицы.

На языке матриц условие разрешимости системы линейных уравнений формулируется в виде теоремы Кронекера-Капелли:

ранг матрицы Понятие Матрицы как математического объекта, операции над матрицами, прменение равен рангу расширенной матрицы ,

составленной из столбцов Понятие Матрицы как математического объекта, операции над матрицами, прменение и столбца .

Важный частный случай. Если количество уравнений совпадает с количеством неизвестных ( Понятие Матрицы как математического объекта, операции над матрицами, прменение , т.е. матрица - квадратная), то условие однозначной разрешимости является равносильным условию обратимости матрицы Понятие Матрицы как математического объекта, операции над матрицами, прменение .

(Замечание. Разрешимость системы еще не влечет невырожденности матрицы. Пример: Понятие Матрицы как математического объекта, операции над матрицами, прменение .)

В частности, если матрица Понятие Матрицы как математического объекта, операции над матрицами, прменение является обратимой, то решение системы может быть записано (а если вычислена , то и найдено) в виде

Понятие Матрицы как математического объекта, операции над матрицами, прменение .

Этот приводит к алгоритму вычисления значений неизвестных по правилу Крамера.

Линейные преобразования[ | ]

Линейное отображение

Рассмотрим линейное преобразование Понятие Матрицы как математического объекта, операции над матрицами, прменение , действующее из -мерного векторного пространства в -мерное векторное пространство Понятие Матрицы как математического объекта, операции над матрицами, прменение , имеющее следующий вид:

$\left\{\begin{array}{rcl}y_1&=&a_{11}x_1 + a_{12}x_2 + \ldots + a_{1n}x_n\\ y_2&=&a_{21}x_1 + a_{22}x_2 + \ldots + a_{2n}x_n\\ & \cdots & \\ y_m&=&a_{m1}x_1 + a_{m2}x_2 + \ldots + a_{mn}x_n\\ \end{array}\right.$ .

В матричной форме это преобразование уравнения вида:

Понятие Матрицы как математического объекта, операции над матрицами, прменение .

Матрица Понятие Матрицы как математического объекта, операции над матрицами, прменение — это матрица коэффициентов линейного преобразования.

Если рассмотреть действие линейного преобразования Понятие Матрицы как математического объекта, операции над матрицами, прменение на векторы вида

Понятие Матрицы как математического объекта, операции над матрицами, прменение ,

составляющие базис пространства Понятие Матрицы как математического объекта, операции над матрицами, прменение , то — это есть j-ый столбец матрицы .

Таким образом, матрица Понятие Матрицы как математического объекта, операции над матрицами, прменение полностью описывает линейное преобразование , и, поэтому, называется матрицей линейного преобразования.

Определения[ | ]

Прямоугольная матрица[ | ]

Пусть есть два конечных множества:

номера строк: ;

номера столбцов: , где и — натуральные числа.

Назовем матрицей Понятие Матрицы как математического объекта, операции над матрицами, прменение размера (читается на ) ( - строк, - столбцов) с элементами из некоторого кольца или поля Понятие Матрицы как математического объекта, операции над матрицами, прменение отображение вида . Матрица записывается как

Понятие Матрицы как математического объекта, операции над матрицами, прменение

где элемент матрицы Понятие Матрицы как математического объекта, операции над матрицами, прменение находится на пересечении -й строки и -го столбца.

-я строка матрицы
-й столбец матрицы

При этом количество элементов матрицы равно Понятие Матрицы как математического объекта, операции над матрицами, прменение .

В соответствии с этим

каждую строку матрицы можно интерпретировать как вектор в -мерном координатном пространстве ;
каждый столбец матрицы — как вектор в -мерном координатном пространстве .

Сама матрица естественным образом интерпретируется как вектор в пространстве Понятие Матрицы как математического объекта, операции над матрицами, прменение , имеющем размерность . Это позволяет ввести покомпонентное сложение матриц и умножение матрицы на число (см. ниже); что касается матричного умножения, то оно существенным образом опирается на прямоугольную структуру матрицы.

Квадратная матрица[ | ]

Если у матрицы количество строк Понятие Матрицы как математического объекта, операции над матрицами, прменение совпадает с количеством столбцов , то такая матрица называется квадратной, а число Понятие Матрицы как математического объекта, операции над матрицами, прменение называется размером квадратной матрицы или ее порядком.

Вектор-строка и вектор-столбец[ | ]

Матрицы размера Понятие Матрицы как математического объекта, операции над матрицами, прменение и являются элементами пространств и соответственно:

матрица размера называется вектор-столбцом и имеет специальное обозначение:

$\mathrm{colon}\,(a_1,\dots,a_i,\dots,a_m) =\left( \begin{array}{c}a_1 \\ \vdots \\ a_i \\ \vdots \\ a_m \end{array} \right) =(a_1,\dots,a_i,\dots,a_m)^{T};$

матрица размера называется вектор-строкой и имеет специальное обозначение:

Понятие Матрицы как математического объекта, операции над матрицами, прменение

Элементарные преобразования матриц

Элементарными преобразованиями строк матрицы называются следующие преобразования:

Умножение строки на число отличное от нуля,
Прибавление одной строки к другой строке,
Перестановка местами двух строк.

Элементарные преобразования столбцов матрицы определяются аналогично.

Ранг матрицы[ | ]

Ранг матрицы

Строки и столбцы матрицы являются элементами соответствующих векторных пространств:

столбцы матрицы составляют элементы пространства размерности ;
строки матрицы составляют элементы пространства размерности .

Рангом матрицы называют количество линейно независимых столбцов матрицы (столбцовый ранг матрицы) или количество линейно независимых строк матрицы (строчный ранг матрицы). Этому определению эквивалентно определение ранга матрицы как порядка максимального отличного от нуля минора матрицы.

При элементарных преобразованиях ранг матрицы не меняется.

Обозначения[ | ]

Обычно матрицу обозначают заглавной буквой латинского алфавита: пусть

Понятие Матрицы как математического объекта, операции над матрицами, прменение

тогда Понятие Матрицы как математического объекта, операции над матрицами, прменение — матрица, которая интерпретируется как прямоугольный массив элементов поля вида Понятие Матрицы как математического объекта, операции над матрицами, прменение , где

первый индекс означает индекс строки: ;
второй индекс означает индекс столбца: ;

таким образом, Понятие Матрицы как математического объекта, операции над матрицами, прменение — элемент матрицы , находящийся на пересечении -й строки и -го столбца. В соответствии с этим принято следующее компактное обозначение для матрицы размера Понятие Матрицы как математического объекта, операции над матрицами, прменение :

Понятие Матрицы как математического объекта, операции над матрицами, прменение

или просто

Понятие Матрицы как математического объекта, операции над матрицами, прменение

если нужно просто указать обозначение для элементов матрицы.

Иногда, вместо Понятие Матрицы как математического объекта, операции над матрицами, прменение , пишут , чтобы отделить индексы друг от друга и избежать смешения с произведением двух чисел.

Если необходимо дать развернутое представление матрицы в виде таблицы, то используют запись вида

$\begin{pmatrix} a_{11} & \cdots & a_{1j} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ a_{i1} & \cdots & a_{ij} & \cdots & a_{in} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ a_{m1} & \cdots & a_{mj} & \cdots & a_{mn} \end{pmatrix},\quad\left[\begin{array}{ccccc} a_{11} & \cdots & a_{1j} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ a_{i1} & \cdots & a_{ij} & \cdots & a_{in} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ a_{m1} & \cdots & a_{mj} & \cdots & a_{mn} \end{array}\right],\quad\left\|\begin{array}{ccccc} a_{11} & \cdots & a_{1j} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ a_{i1} & \cdots & a_{ij} & \cdots & a_{in} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ a_{m1} & \cdots & a_{mj} & \cdots & a_{mn} \end{array}\right\|$

Можно встретить как обозначения с круглыми скобками «(…)», так и обозначения с квадратными скобками «[…]». Реже можно встретить обозначения с двойными прямыми линиями «||…||»).

Поскольку матрица состоит из строк и столбцов, для них используются следующие обозначения:

$a_{i\cdot}=A_i=[ \begin{array}{ccccc} a_{i1} & \cdots & a_{ij} & \cdots & a_{in} \\ \end{array}]$ — это Понятие Матрицы как математического объекта, операции над матрицами, прменение -я строка матрицы ,

$a_{\cdot j}=A^j=\left[ \begin{array}{c} a_{1j}\\\vdots \\a_{ij} \\\vdots \\a_{mj} \\ \end{array}\right]$ — это Понятие Матрицы как математического объекта, операции над матрицами, прменение -й столбец матрицы .

Таким образом, матрица обладает двойственным представлением — по столбцам:

$A=[ \begin{array}{ccccc} A^{1} & \cdots & A^{j} & \cdots & A^{n} \\ \end{array}]$

и по строкам:

$A=\left[ \begin{array}{c} A_{1}\\\vdots \\A_{i} \\\vdots \\A_{m} \\ \end{array}\right]$ .

Такое представление позволяет формулировать свойства матриц в терминах строк или в терминах столбцов.

Транспонированная матрица

Для каждой матрицы Понятие Матрицы как математического объекта, операции над матрицами, прменение размера

можно построить матрицу Понятие Матрицы как математического объекта, операции над матрицами, прменение размера ,

у которой Понятие Матрицы как математического объекта, операции над матрицами, прменение для всех и .

Такая матрица называется транспонированной матрицей для Понятие Матрицы как математического объекта, операции над матрицами, прменение и обозначается ,

иногда (если нет возможности спутать с дифференцированием) обозначается Понятие Матрицы как математического объекта, операции над матрицами, прменение ,

иногда (если нет возможности спутать с эрмитовым сопряжением) обозначается Понятие Матрицы как математического объекта, операции над матрицами, прменение .

При транспонировании строки (столбцы) матрицы Понятие Матрицы как математического объекта, операции над матрицами, прменение становятся столбцами (соответственно - строками) матрицы .

Очевидно, Понятие Матрицы как математического объекта, операции над матрицами, прменение .

Для матриц над кольцом Понятие Матрицы как математического объекта, операции над матрицами, прменение транспонирование является изоморфизмом - модулей матриц, поскольку

Понятие Матрицы как математического объекта, операции над матрицами, прменение ,

Понятие Матрицы как математического объекта, операции над матрицами, прменение , для любых .

Диагональная матрица[ | ]

Диагональная матрица — квадратная матрица, все элементы которой кроме диагональных — нулевые Понятие Матрицы как математического объекта, операции над матрицами, прменение , иногда записывается как:

Понятие Матрицы как математического объекта, операции над матрицами, прменение

Единичная матрица[ | ]

Единичная матрица — матрица, при умножении на которую любая матрица (или вектор) остается неизменной, является диагональной матрицей с единичными (всеми) диагональными элементами:

Понятие Матрицы как математического объекта, операции над матрицами, прменение

Для ее обозначения чаще всего используется обозначение I или E, а также просто 1 (или 1 специальным шрифтом).

Для обозначения ее элементов также используется символ Кронекера Понятие Матрицы как математического объекта, операции над матрицами, прменение , определяемый как:

Понятие Матрицы как математического объекта, операции над матрицами, прменение

Понятие Матрицы как математического объекта, операции над матрицами, прменение при

Нулевая матрица[ | ]

Для обозначения нулевой матрицы — матрицы, все элементы которой нули (при сложении ее с любой матрицей та остается неизменной, а при умножении на любую получается нулевая матрица) — используется обычно просто 0 или 0 специальным шрифтом, или буква, начертанием похожая на ноль, например Понятие Матрицы как математического объекта, операции над матрицами, прменение .

операции над матрицами

Действия над матрицами

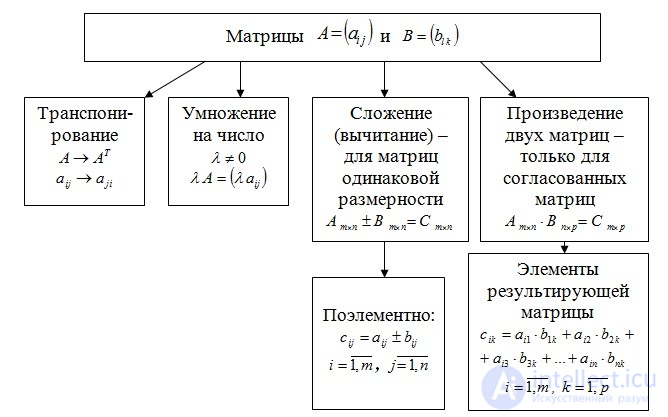
Понятие Матрицы как математического объекта, операции над матрицами, прменение

Сложение матриц[ | ]

Складывать можно только матрицы одинакового размера.

Сложение матриц Понятие Матрицы как математического объекта, операции над матрицами, прменение есть операция нахождения матрицы , все элементы которой равны попарной сумме всех соответствующих элементов матриц Понятие Матрицы как математического объекта, операции над матрицами, прменение и , то есть каждый элемент матрицы равен

Понятие Матрицы как математического объекта, операции над матрицами, прменение

Свойства сложения матриц:

коммутативность: A+B = B+A;
ассоциативность: (A+B)+C =A+(B+C);
сложение с нулевой матрицей: A + Θ = A;
существование противоположной матрицы: A + (-A) = Θ;

Все свойства линейных операций повторяют аксиомы линейного пространства и поэтому справедлива теорема:

Множество всех матриц одинаковых размеров mxn с элементами из поля P (поля всех действительных или комплексных чисел) образует линейное пространство над полем P (каждая такая матрица является вектором этого пространства). Об этом говорит сайт https://intellect.icu . Впрочем, прежде всего во избежание терминологической путаницы, матрицы в обычных контекстах избегают без необходимости (которой нет в наиболее обычных стандартных применениях) и четкого уточнения употребления термина называть векторами.

Умножение матрицы на число[ | ]

Умножение матрицы Понятие Матрицы как математического объекта, операции над матрицами, прменение на число заключается в построении матрицы .

Свойства умножения матриц на число:

умножение на единицу: 1A = A;
ассоциативность: (λβ)A = λ(βA);
дистрибутивность: (λ+β)A = λA + βA;
дистрибутивность: λ(A+B) = λA + λB;

Умножение матриц[ | ]

Понятие Матрицы как математического объекта, операции над матрицами, прменение

Умножение матриц (обозначение: Понятие Матрицы как математического объекта, операции над матрицами, прменение , реже со знаком умножения ) — есть операция вычисления матрицы , каждый элемент которой равен сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

Понятие Матрицы как математического объекта, операции над матрицами, прменение

Количество столбцов в матрице Понятие Матрицы как математического объекта, операции над матрицами, прменение должно совпадать с количеством строк в матрице , иными словами, матрица обязана быть согласованной с матрицей Понятие Матрицы как математического объекта, операции над матрицами, прменение . Если матрица имеет размерность , — , то размерность их произведения есть .

Свойства умножения матриц:

ассоциативность: (AB)C = A(BC);
некоммутативность (в общем случае): AB BA;
произведение коммутативно в случае умножения с единичной матрицей: AI = IA;
дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC;
ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB);

Умножение вектора на матрицу[ | ]

По обычным правилам матричного умножения вектор-столбец умножается на матрицу, которая записывается слева от него, а вектор-строка умножается на матрицу, которая записывается справа от нее. Поскольку элементы вектора-столбца или вектора-строки можно записать (что обычно и делается), используя один, а не два индекса, это умножение можно записать так:

для вектора-столбца v (получая новый вектор-столбец Av):

Понятие Матрицы как математического объекта, операции над матрицами, прменение

для вектора-строки s (получая новый вектор-строку sA):

Понятие Матрицы как математического объекта, операции над матрицами, прменение

Вектор-строка, матрица и вектор-столбец могут быть умножены друг на друга, давая число (скаляр):

Понятие Матрицы как математического объекта, операции над матрицами, прменение

(Порядок важен: вектор-строка слева, вектор-столбец справа от матрицы).

Эти операции являются основой матричного представления линейных операторов и линейных преобразований координат (смены базисов), таких, как повороты, масштабирования, зеркальные отражения, а также (последнее) матричного представления билинейных (квадратичных) форм.

При представлении вектора вещественного векторного пространства в ортонормированном базисе (что эквивалентно использованию прямоугольных декартовых координат) соответствующие ему вектор-столбец и вектор-строка, представляющие собой набор компонент вектора, будут совпадать (поэлементно), отличаясь лишь формально своим изображением для корректности матричных операций (то есть один получается из другого просто операцией транспонирования). При использовании же неортонормированных базисов (например, косоугольных координат или хотя бы разных масштабов по осям) вектор-столбец соответствует компонентам вектора в основном базисе, а вектор-строка — в базисе, дуальном основному (Иногда о пространстве векторов-строк говорят также как об особом, дуальном пространству векторов-столбцов, пространстве ковекторов).

Заметим, что обычной мотивировкой введения матриц и определения операции матричного умножения (см.тж.в статье об умножении матриц) является именно введение их, начиная с умножения вектора на матрицу (которое вводится исходя из преобразований базиса или вообще линейных операций над векторами), а уже затем композиции преобразований сопоставляется произведение матриц. Действительно, если новый вектор Av, полученный из исходного вектора v преобразованием, представимым умножением на матрицу A, преобразовать теперь еще раз, преобразованием, представимым умножением на матрицу B, получив B(Av), то, исходя из правила умножения вектора на матрицу, приведенного в начале этого параграфа (используя ассоциативность умножения чисел и меняя порядок суммирования), нетрудно увидеть в результате формулу, дающую элементы матрицы (BA), представляющую композицию первого и второго преобразований и совпадающую с обычным определением матричного умножения.

Комплексное сопряжение[ | ]

Если элементами матрицы Понятие Матрицы как математического объекта, операции над матрицами, прменение являются комплексные числа, то комплексно сопряженная (не путать с эрмитово сопряженной! см. далее) матрица равна Понятие Матрицы как математического объекта, операции над матрицами, прменение . Здесь — число, комплексно сопряженное к .

Транспонирование и эрмитово сопряжение[ | ]

Транспонирование уже обсуждалось выше: если Понятие Матрицы как математического объекта, операции над матрицами, прменение , то . Для комплексных матриц более употребительно эрмитово сопряжение: . С точки зрения операторного взгляда на матрицы, транспонированная и эрмитово сопряженная матрица — это матрицы оператора, сопряженного относительно скалярного или эрмитова произведения, соответственно.

Миноры[ | ]

След я: След матрицы

Для квадратной матрицы Понятие Матрицы как математического объекта, операции над матрицами, прменение сумма диагональных элементов (т.е. главных миноров первого порядка) называется следом:

Понятие Матрицы как математического объекта, операции над матрицами, прменение

(другие обозначения Понятие Матрицы как математического объекта, операции над матрицами, прменение , , ).

Свойства:

Если определены и , то .
След является инвариантом преобразований подобия матрицы, т.е. если невырождена, то .
След равен сумме (всех, с учетом кратности) собственных значений матрицы: . Более того, для любого целого (положительного) числа выполняется .

Определитель (детерминант)[ | ]

Определитель

Пусть матрица Понятие Матрицы как математического объекта, операции над матрицами, прменение - квадратная, тогда обозначение определителя: . Если матрица , то

Перманент[ | ]

Перманент

Связанные понятия[ | ]

Линейные комбинации[ | ]

В векторном пространстве линейной комбинацией векторов Понятие Матрицы как математического объекта, операции над матрицами, прменение называется вектор

Понятие Матрицы как математического объекта, операции над матрицами, прменение

где Понятие Матрицы как математического объекта, операции над матрицами, прменение — коэффициенты разложения:

если все коэффициенты равны нулю, то такая комбинация называется тривиальной,
если же хотя бы один коэффициент отличен от нуля, то такая комбинация называется нетривиальной.

Это позволяет описать произведение Понятие Матрицы как математического объекта, операции над матрицами, прменение матриц и терминах линейных комбинаций:

столбцы матрицы — это линейные комбинации столбцов матрицы с коэффициентами, взятыми из матрицы ;
строки матрицы — это линейные комбинации строк матрицы с коэффициентами, взятыми из матрицы .

Линейная зависимость[ | ]

Если какой-либо вектор можно представить в виде линейной комбинации, то говорят о линейной зависимости данного вектора от элементов комбинации.

Точнее, говорят так: некоторая совокупность элементов векторного пространства называется линейно зависимой, если существует равная нулю линейная комбинация элементов данной совокупности или

Понятие Матрицы как математического объекта, операции над матрицами, прменение

где не все числа Понятие Матрицы как математического объекта, операции над матрицами, прменение равны нулю; если такой нетривиальной комбинации не существует, то данная совокупность векторов называется линейно независимой.

Линейная зависимость векторов означает, что какой-то вектор заданной совокупности линейно выражается через остальные векторы.

Каждая матрица представляет собой совокупность векторов (одного и того же пространства). Две такие матрицы — две совокупности. Если каждый вектор одной совокупности линейно выражается через векторы другой совокупности, то на языке теории матриц этот факт описывается при помощи произведения матриц:

если строки матрицы линейно зависят от строк матрицы , то для некоторой матрицы ;
если столбцы матрицы линейно зависят от столбцов другой матрицы , то для некоторой матрицы .

Свойства[ | ]

Матричные операции[ | ]

Сложение и вычитание допускается только для матриц одинакового размера.

Существует нулевая матрица Понятие Матрицы как математического объекта, операции над матрицами, прменение такая, что ее прибавление к другой матрице A не изменяет A, то есть

Понятие Матрицы как математического объекта, операции над матрицами, прменение

Все элементы нулевой матрицы равны нулю.

Возводить в степень можно только квадратные матрицы.

Ассоциативность сложения:
Коммутативность сложения:
Ассоциативность умножения:
Вообще говоря, умножение матриц некоммутативно: . Используя это свойство, вводят коммутатор матриц.
Дистрибутивность умножения относительно сложения:
С учетом упомянутых выше свойств, матрицы образуют кольцо относительно операций сложения и умножения.
Свойства операции транспонирования матриц:

, если обратная матрица существует.

Примеры Список матриц

Здесь собраны наиболее важные классы матриц, используемые в математике, науке (в целом) и прикладной науке (в частности).

Под матрицей понимается прямоугольный массив чисел, называемых элементами. Матрицы имеют длинную историю исследований и приложений, что приводит к различным способам их классификации. Первая группа матриц удовлетворяет конкретным условиям и ограничениям на их элементы, включая постоянные матрицы. Важный пример матриц такого вида доставляет единичная матрица:

Понятие Матрицы как математического объекта, операции над матрицами, прменение

Обозначается также буквой E. Другие способы классификации матриц связаны либо с их собственными значениями, либо с условиями в виде матричных уравнений (соотношений). Наконец, во многих областях (в физике и в химии) встречаются матрицы специального вида, которые применяются исключительно в этих областях.

Матрицы, определяемые условиями на элементы[ | ]

Данный ниже список матриц определяется условиями, которые накладываются на элементы матриц. Многие из таких свойств оказываются применимыми только к квадратным матрицам. В квадратной матрице имеются две диагонали: главная диагональ (идущая из левого верхнего угла в правый нижний угол) и побочная диагональ (идущая из левого нижнего угла в правый верхний угол).

Матрицы общего вида[ | ]

Матрицы, представленные ниже, характеризуются тем, что условия на элементы матриц описываются в терминах структуры матрицы. Сюда относится взаимное расположение ненулевых элементов, а также свойства инвариантности относительно матричных преобразований.

Название	Описание	Примечания, пояснения
Бинарная матрица	Матрица, состоящая из нулей и единиц.	Синонимы: булевская матрица, логическая матрица.
Матрица альтернанса	Матрица, элементы которой представляют собой значения функций в определенных точках.
Нулевая матрица	Матрица, полностью состоящая из нулей.
Антидиагональная матрица	Квадратная матрица, все элементы которой, лежащие вне побочной диагонали, равны нулю.
Антиэрмитова матрица	Квадратная матрица с комплексными элементами, переходящая в себя с изменением знака при операции эрмитова сопряжения (то есть при комплексном сопряжении каждого элемента и последующем транспонировании матрицы),	Синоним косо-эрмитовой матрицы.
Антисимметричная матрица		Синоним кососимметричной матрицы.
Стрелочная матрица (англ.)	Квадратная матрица, все ненулевые элементы которой являются элементами первого столбца, первой строки или главной диагонали.
Ленточная матрица (англ.)	Квадратная матрица, все ненулевые элементы которой примыкают к главной диагонали.
Бидиагональная матрица (англ.)	Матрица, все ненулевые элементы которой находятся на главной диагонали и на одной из под- или наддиагонали.
Бисимметричная матрица	Квадратная матрица, симметричная как относительно главной диагонали, так и относительно побочной диагонали.
Блочно-диагональная матрица	Блочная матрица, у которой имеются матрицы только на главной диагонали.
Блочная матрица	Матрица, которая разбита на подматрицы, называемые блоками.
Блочно-трехдиагональная матрица (англ.)	Блочная матрица, чьи блоки организованы так же, как у трехдиагональной матрицы.
Булевская матрица		синоним для (0,1)-матрицы, бинарной матрицы и логической матрицы.
Матрица Коши	Матрица, каждый элемент которой имеет вид где и — две инъективные последовательности
Центросимметричная матрица	Матрица, симметричная относительно своего центра, то есть:
Конференс-матрица	Квадратная матрица с нулевыми элементами на диагонали и элементами вида +1 и −1 вне диагонали, такая, что — единичная матрица.
Комплексная матрица Адамара (англ.)	Матрица, все строки и столбцы которой попарно ортогональны друг другу, а сами элементы унимодулярны.
Положительно полуопределенная матрица	Квадратная матрица с вещественными элементами такая, что квадратичная форма оказывается неотрицательной для каждого неотрицательного .
Диагонально доминирующая матрица	Матрица, элементы которой удовлетворяют указанному здесь условию:
Диагональная матрица	Матрица, у которой все элементы вне главной диагонали равны нулю.
Элементарная матрица (англ.)	Матрица, которая получается из единичной при помощи элементарных преобразований.
Эквивалентная матрица (англ.)	Матрица, которая получается из другой матрицы при помощи элементарных преобразований над строками или столбцами.
Матрица Фробениуса	Матрица, которая получается из единичной при помощи сдвига и добавления нового столбца.
Эрмитова матрица, эрмитово-самосопряженная матрица	Квадратная матрица с комплексными элементами, переходящая в себя при операции эрмитова сопряжения (то есть при комплексном сопряжении каждого элемента и последующем транспонировании матрицы),
Неотрицательная матрица	Матрица, все элементы которой неотрицательны.
Матрица перестановки	Квадратная матрица, в которой в каждом столбце и в каждой строке стоит ровно одна единица, а остальные нули. Является матричным представлением перестановки.
Обобщенная матрица перестановки (англ.)	Квадратная матрица с ровно одним ненулевым элементом в каждой строке и в каждом столбце.
Персимметричная матрица	Матрица, симметричная относительно побочной диагонали:
Полиномиальная матрица	Матрица, все элементы которой суть полиномы.
Положительная матрица	Матрица, все элементы которой положительны.
Матрица кватернионов	Матрица, все элементы которой представляют собой кватернионы.
Матрица знака (англ.)	Матрица, все элементы которой равны 1, 0 или −1.
Матрица сигнатуры (англ.)	Матрица, все элементы которой равны либо 1, либо −1.
Косоэрмитова матрица	Квадратная комплексная матрица, которая меняет знак при эрмитовом сопряжении.	То же, что и антиэрмитова матрица.
Кососимметричная матрица	Квадратная матрица, которая меняет знак при транспонировании,	То же, что и антисимметричная матрица.
Небесная матрица (англ.)	Ленточная матрица, реорганизованная таким образом, чтобы уменьшить занимаемое пространство.
Разреженная матрица	Матрица, практически полностью состоящая из нулей.	Алгоритмы для разреженных матриц позволяют обрабатывать бо́льшие матрицы, чем для плотных
Матрица Сильвестра	Квадратная матрица, чьи элементы — это коэффициенты двух полиномов.	Матрица Сильвестра не вырождена тогда и только тогда, когда два полинома взаимно просты.
Симметричная матрица	Квадратная матрица, которая совпадает со своей транспонированной: ().
Теплицева матрица	Матрица, у которой на диагоналях стоят одни и те же элементы.
Треугольная матрица	Матрица, у которой все элементы выше главной диагонали нулевые (нижнетреугольная матрица), или матрица, у которой все элементы ниже главной диагонали нулевые (верхнетреугольная матрица).
Трехдиагональная матрица	Матрица, у которой все ненулевые элементы располагаются на трех диагоналях: главной, первой сверху и первой снизу.
Унитарная матрица	Квадратная комплексная матрица, обращение которой дает эрмитово-сопряженную матрицу,
Специальная унитарная матрица	Унитарная матрица, определитель которой равен единице
Матрица Вандермонда	Матрица, строки (или столбцы) которой представляют собой последовательные степени: 1, a, a2, a3, …, an
Матрица Уэлша (англ.)	Квадратная матрица размера, равного степени двойки, состоящая из элементов +1 или −1.
Z-матрица	Матрица, все недиагональные элементы которой меньше нуля.
Ганкелева матрица	Квадратная матрица, у которой на каждой побочной диагонали стоят равные элементы.

Постоянные матрицы[ | ]

Матрицы, представленные ниже, характеризуются тем, что их элементы являются одними и теми же для всех возможных размеров матриц.

Название	Описание	Условия на элементы	Примечания
Обменная матрица	Бинарная матрица, у которой на побочной диагонали стоят единицы, а все остальные элементы нулевые.		См. Матрица перестановки.
Матрица Гильберта			См. Ганкелева матрица.
Единичная матрица	Квадратная матрица, у которой на главной диагонали стоят единицы, а остальные элементы равны нулю.
Матрица Лемера		aij = min(i, j) ÷ max(i, j)	См. положительную симметричную матрицу.
Матрица единиц	Матрица, все элементы которой суть единицы.
Матрица Паскаля	Матрица, состоящая из элементов треугольника Паскаля.
Матрица Паули	Блочная матрица, состоящая из блоков размера 2 × 2, каждый из которых представляет собой комплексную эрмитовую и унитарную матрицу.
Матрица Редхеффера		aij = 1, если i делится на j или если j = 1; в противном случае, aij = 0.	См. (0, 1)-матрица.
Матрица сдвига	Матрица, у которой на одной из побочных диагоналях стоят единицы, а остальные элементы нулевые.	или	Умножением на эту матрицу элементы сдвигаются на одну позицию.
Нулевая матрица	Матрица, у которой все элементы нулевые.

Преобразованные матрицы[ | ]

Обратная матрица
Транспонированная матрица
Эрмитово-сопряженная матрица
Присоединенная матрица

Матрицы, удовлетворяющие условиям на произведения или обратные матрицы[ | ]

Название	Описание	Примечания
Идемпотентная матрица	Матрица A обладающая свойством A² = AA = A.
Обратимая матрица	Квадратная, имеющая обратную, то есть, такую матрицу B, что AB = BA = I.	Обратимые матрицы образуют общую линейную группу.
Инволютивная матрица	Квадратная матрица A, обратная самой себе, то есть AA = I.
Нильпотентная матрица	Квадратная матрица A такая, что Aq = 0 для некоторого положительного q.	Эквивалентно, все собственные значения A равны 0.
Нормальная матрица	Квадратная матрица, коммутирующая со своей эрмитово-сопряженной: AA∗ = A∗A	Для таких матриц справедлива спектральная теорема.
Ортогональная матрица	Матрица, обратная своей транспонированной: A−1 = AT.	Такие матрицы образуют ортогональную группу.
Ортонормированная матрица	Матрица, столбцы которой являются ортонормированными векторами.
Сингулярная матрица	Квадратная матрица, которая не является обратимой.
Унимодулярная матрица	Квадратная матрица с целыми коэффициентами, определитель которой равен +1 или −1.
Унипотентная матрица	Квадратная матрица, все собственные значения равны 1.	Эквивалентно, A − I нильпотентна. Вау!! 😲 Ты еще не читал? Это зря! унипотентная группа.
Вполне унимодулярная матрица	Матрица, любая несингуляная подматрица которой является унимодулярной.	Используется линейном программировании при релаксации целых программ.
Весовая матрица	Квадратная матрица, элементы которой принадлежат множеству {0, 1, −1}, так что AAT = wI для некоторого целого w.

Матрицы, используемые в теории графов

Матрица смежности
Матрица бисмежности
Матрица степени
Матрица Эдмондса
Матрица инцидентности
Матрица Кирхгофа (матрица Лапласа)
Матрица смежности Зейделя
Матрица Татта

Матрицы, используемые в физике[ | ]

Матрицы Кабибо-Кобаяши-Москавы
Гамма матрицы Дирака
Матрицы Паули
Матрицы Гелл-Манна
S-матрица
Матрица плотности

Квадратная матрица и смежные определения[ | ]

Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.

Для квадратных матриц существует единичная матрица Понятие Матрицы как математического объекта, операции над матрицами, прменение (аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на нее не влияет на результат, а именно

Понятие Матрицы как математического объекта, операции над матрицами, прменение

У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю

Понятие Матрицы как математического объекта, операции над матрицами, прменение

Для некоторых квадратных матриц можно найти так называемую обратную матрицу. Обратная матрица Понятие Матрицы как математического объекта, операции над матрицами, прменение такова, что если матрицу умножить на обратную ей матрицу, то получится единичная матрица:

Понятие Матрицы как математического объекта, операции над матрицами, прменение

Обратная матрица существует не всегда. Матрицы, для которых обратная матрица существует, называются невырожденными (или регулярными), а для которых нет — вырожденными (или сингулярными). Матрица невырождена, если все ее строки (столбцы) линейно независимы как векторы. Максимальное число линейно независимых строк (столбцов) называется рангом матрицы. Определителем (детерминантом) матрицы называется значение нормированной кососимметрической (антисимметрической) полилинейной формы валентности Понятие Матрицы как математического объекта, операции над матрицами, прменение на столбцах матрицы. Квадратная матрица над числовым полем вырождена тогда и только тогда, когда ее определитель равен нулю.

Кольцо матриц[ | ]

Из указанных выше свойств сложения и умножения матриц (ассоциативность и коммутативность сложения, дистрибутивность умножения, существование нулевой и противоположной по сложению матрицы) следует, что квадратные матрицы n на n с элементами из любого кольца R образуют кольцо, изоморфное кольцу эндоморфизмов свободного модуля Rn. Это кольцо обозначается Понятие Матрицы как математического объекта, операции над матрицами, прменение или . Если же R — коммутативное кольцо, является также ассоциативной алгеброй над R. Определитель матрицы с элементами из коммутативного кольца можно вычислять по обычной формуле, при этом матрица будет обратима тогда и только тогда, когда ее определитель обратим в R. Это обобщает ситуацию с матрицами с элементами из поля, так как в поле обратим любой элемент, кроме нуля.

Матрицы в теории групп[ | ]

Матрицы играют важную роль в теории групп. Они используются при построении общих линейных групп, специальных линейных групп, диагональных групп, треугольных групп, унитреугольных групп.

Конечную группу (в частности, симметрическую) можно (изоморфно) промоделировать матрицами перестановок (содержащими только «0» и «1»),

например, для Понятие Матрицы как математического объекта, операции над матрицами, прменение : $\begin{pmatrix} 1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{pmatrix}$ , $\begin{pmatrix} 0 & 1 & 0\\0 & 0 & 1\\1 & 0 & 0\end{pmatrix}$ , $\begin{pmatrix} 0 & 0 & 1\\1 & 0 & 0\\0 & 1 & 0\end{pmatrix}$ , $\begin{pmatrix} 0 & 1 & 0\\1 & 0 & 0\\0 & 0 & 1\end{pmatrix}$ , $\begin{pmatrix} 0 & 0 & 1\\0 & 1 & 0\\1 & 0 & 0\end{pmatrix}$ , $\begin{pmatrix} 1 & 0 & 0\\0 & 0 & 1\\0 & 1 & 0\end{pmatrix}$ .

Поле Понятие Матрицы как математического объекта, операции над матрицами, прменение комплексных чисел может быть (изоморфно) промоделировано над полем вещественных чисел:

для Понятие Матрицы как математического объекта, операции над матрицами, прменение матричные аналоги $Z = \begin{pmatrix} x & y\\-y & x \end{pmatrix}$ , $C = \begin{pmatrix} a & b\\-b & a \end{pmatrix}$ , где ;

Понятие Матрицы как математического объекта, операции над матрицами, прменение соответствует $Z + C = \begin{pmatrix} x + a & y + b\\- y - b & x + a\end{pmatrix}$ ;

Понятие Матрицы как математического объекта, операции над матрицами, прменение соответствует $Z C = \begin{pmatrix} x a - y b & x b + y a\\- y a - x b & - y b + x a\end{pmatrix}$ ;

Понятие Матрицы как математического объекта, операции над матрицами, прменение соответствует $Z^T = \begin{pmatrix} x & -y\\y & x \end{pmatrix}$ ;

Понятие Матрицы как математического объекта, операции над матрицами, прменение ;

$\frac{1}{z} = \frac{\bar{z}}{z \bar{z}} = \frac{x - i y}{x^2 + y^2}$ при $z \ne 0$ соответствует $Z^{-1} = \frac{Z^T}{det(Z)}$ при Понятие Матрицы как математического объекта, операции над матрицами, прменение ;

Понятие Матрицы как математического объекта, операции над матрицами, прменение соответствует $e^x \begin{pmatrix} cos(y) & sin(y)\\-sin(y) & cos(y) \end{pmatrix}$ .

В частности, для $E = \begin{pmatrix} 1 & 0\\0 & 1 \end{pmatrix}$ , $I = \begin{pmatrix} 0 & 1\\-1 & 0 \end{pmatrix}$

$z = x + i y \in \mathbb{C}$ соответствует Z = x E + y I ,

где Понятие Матрицы как математического объекта, операции над матрицами, прменение .

Замечание. Модель имеет автоморфизм Понятие Матрицы как математического объекта, операции над матрицами, прменение , то есть

Тело кватернионов Понятие Матрицы как математического объекта, операции над матрицами, прменение может быть (изоморфно) промоделировано над полем вещественных чисел:

для Понятие Матрицы как математического объекта, операции над матрицами, прменение матричный аналог $Q = \begin{pmatrix} t & x & y & -z\\ -x & t & -z & -y\\ -y & z & t & x\\ z & y & -x & t \end{pmatrix}$ , где .

Для того, чтобы кватерниону Понятие Матрицы как математического объекта, операции над матрицами, прменение соответствовала матрица ,

где Понятие Матрицы как математического объекта, операции над матрицами, прменение , IJ=-JI=K , JK=-KJ=I , KI=-IK=J ,

можно ввести базисные элементы

$E = \begin{pmatrix} 1 & 0 & 0 & 0\\0 & 1 & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & 0 & 1\end{pmatrix}$ , $I = \begin{pmatrix} 0 & a & 0 & 0\\-a & 0 & 0 & 0\\0 & 0 & 0 & b\\0 & 0 & -b & 0\end{pmatrix}$ , $J = \begin{pmatrix} 0 & 0 & c & 0\\0 & 0 & 0 & d\\-c & 0 & 0 & 0\\0 & -d & 0 & 0\end{pmatrix}$ , $K = \begin{pmatrix} 0 & 0 & 0 & ad\\0 & 0 & -ac & 0\\0 & -bd & 0 & 0\\bc & 0 & 0 & 0\end{pmatrix}$ .

Параметры должны удовлетворять условиям: Понятие Матрицы как математического объекта, операции над матрицами, прменение и .

Существует 8 решений (8 представлений).

Вау!! 😲 Ты еще не читал? Это зря!

Норма матрицы
Определитель матрицы
Собственные векторы, значения и пространства
Массив — тип данных в программировании, соответствующий матрице (многомерность достигается вложенными массивами).
Разреженный массив — одна из компьютерных форм представления разреженных матриц.
Линейные матричные неравенства — аппарат для решения задач синтеза законов управления.
Лямбда-матрица
Жорданова нормальная форма
Список матриц

Исследование, описанное в статье про матрица, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое матрица, операции над матрицами, транспонирование и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Линейная алгебра и аналитическая геометрия

Понятие Матрицы как математического объекта, операции над матрицами, прменение

История[ | ]

Введение[ | ]

Системы линейных уравнений

Линейные преобразования[ | ]

Определения[ | ]

Прямоугольная матрица[ | ]

Квадратная матрица[ | ]

Вектор-строка и вектор-столбец[ | ]

Элементарные преобразования матриц

Ранг матрицы[ | ]

Обозначения[ | ]

Транспонированная матрица

Диагональная матрица[ | ]

Единичная матрица[ | ]

Нулевая матрица[ | ]

операции над матрицами

Сложение матриц[ | ]

Умножение матрицы на число[ | ]

Умножение матриц[ | ]

Умножение вектора на матрицу[ | ]

Комплексное сопряжение[ | ]

Транспонирование и эрмитово сопряжение[ | ]

Миноры[ | ]

След я: След матрицы

Определитель (детерминант)[ | ]

Перманент[ | ]

Связанные понятия[ | ]

Линейные комбинации[ | ]

Линейная зависимость[ | ]

Свойства[ | ]

Матричные операции[ | ]

Примеры Список матриц

Матрицы, определяемые условиями на элементы[ | ]

Матрицы общего вида[ | ]

Постоянные матрицы[ | ]

Преобразованные матрицы[ | ]

Матрицы, удовлетворяющие условиям на произведения или обратные матрицы[ | ]

Матрицы, используемые в теории графов

Матрицы, используемые в физике[ | ]

Квадратная матрица и смежные определения[ | ]

Кольцо матриц[ | ]

Матрицы в теории групп[ | ]

Вау!! 😲 Ты еще не читал? Это зря!

Комментарии

Оставить комментарий

Линейная алгебра и аналитическая геометрия

Термины: Линейная алгебра и аналитическая геометрия