4.5. Эллипс Канонические уравнения эллипса кратко

Привет, мой друг, тебе интересно узнать все про эллипс, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое эллипс, канонические уравнения эллипса , настоятельно рекомендую прочитать все из категории Линейная алгебра и аналитическая геометрия.

эллипс (др.-греч. ἔλλειψις «опущение; нехватка, недостаток (эксцентриситета до 1)») — замкнутая кривая на плоскости, которая может быть получена как пересечение плоскости и кругового цилиндра или как ортогональная проекция окружности на плоскость.

Одной из трех составляющих «Триады Менехма» является Эллипс.
Ее открыл в IV веке до н. э. древнегреческий математик Менехм, пересекая разного вида конусы (остроугольный, прямоугольный и тупоугольный)
плоскостью, перпендикулярной образующей. В итоге ему удалось свести решение задачи об удвоении куба к нахождению точек пересечения двух
парабол. Более столетия конические сечения не имели собственных названий (указывали лишь способ получения кривых, например, эллипс —
«сечение остроугольного конуса»).

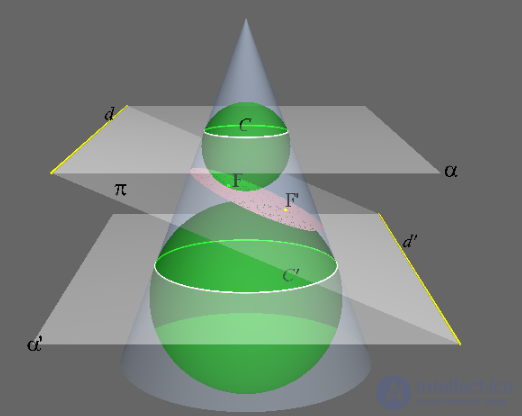
Эллипс как коническое сечение, его фокусы и директрисы, получаемые геометрически с помощью шаров Данделена.

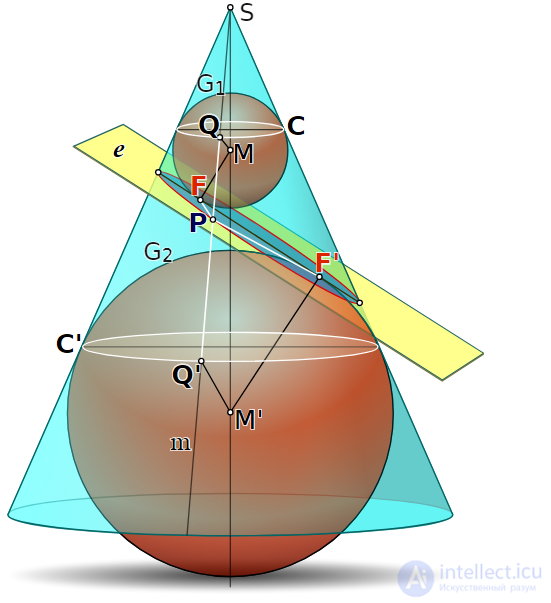
Шары Данделена — сферы, участвующие в геометрическом построении, которое связывает планиметрическое определение эллипса, гиперболы и параболы через фокусы с их стереометрическим определением как сечения конуса. Предложены Данделеном в 1822 году.

Сферы Данделина можно использовать для элегантных современных доказательств двух классических теорем, известных Аполлонию Пергскому . Первая теорема состоит в том, что замкнутое коническое сечение (т.е. эллипс ) - это геометрическое место точек, такое что сумма расстояний до двух фиксированных точек (фокусов) постоянна. Вторая теорема заключается в том, что для любого конического сечения расстояние от фиксированной точки (фокуса) пропорционально расстоянию от фиксированной линии ( директрисы ), а коэффициент пропорциональности называется эксцентриситетом .

Коническое сечение имеет по одной сфере Данделина для каждого фокуса. Эллипс состоит из двух сфер Данделина, соприкасающихся с одной и той же вершиной конуса, в то время как у гиперболы две сферы Данделина касаются противоположных вершин. Парабола имеет только один шары данделена.

Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой.

Эллипс — геометрическое место точек M евклидовой плоскости, для которых сумма расстояний до двух данных точек и (называемых фокусами) постоянна и больше расстояния между фокусами, то есть

, причем .

Другие определения

Эллипс также можно определить как:

• фигуру, которую можно получить из окружности, применяя аффинное преобразование
• ортогональную проекцию окружности на плоскость
• пересечение плоскости и кругового цилиндра.

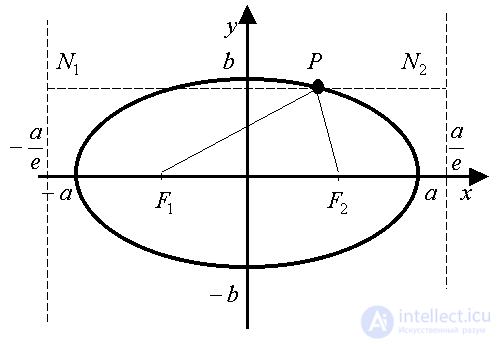
Рис. 5

- каноническое уравнение эллипса (рис. 5),

- большая полуось,

- малая полуось,

- левый и правый фокусы,


- эксцентриситет,

- левая и правая директрисы,

- левый и правый фокальные радиусы точки ,

- расстояния от точки P до левой и правой директрисы.

Приближенные формулы для периметра

Максимальная погрешность этой формулы при эксцентриситете эллипса (соотношение осей ). Об этом говорит сайт https://intellect.icu . Погрешность всегда положительна.

Приблизительно в два раза меньшие погрешности в широком диапазоне эксцентриситетов дает формула: , где Максимальная погрешность этой формулы при эксцентриситете эллипса (соотношение осей {\displaystyle \approx 1/5}) Погрешность также всегда положительна.

Существенно лучшую точность при обеспечивает формула Рамануджана:

При эксцентриситете эллипса (соотношение осей ) погрешность составляет . Погрешность всегда отрицательна.

Еще точней оказалась вторая формула Рамануджана:

Точные формулы для периметра

Джеймс Айвори и Фридрих Бессель независимо друг от друга получили формулу для периметра эллипса:

Альтернативная формула

где — Арифметико-геометрическое среднее 1 и , а — модифицированное арифметико-геометрическое среднее 1 и , которое было введено С. Ф. Адлаем в статье 2012 года.

Площадь эллипса и его сегмента

Площадь эллипса вычисляется по формуле

Площадь сегмента между дугой[en], выпуклой влево, и вертикальной хордой, проходящей через точки и , можно определить по формуле :

Если эллипс задан уравнением , то площадь можно определить по формуле

Другие свойства

• Оптические
  • Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.
  • Свет от источника, находящегося вне любого из фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.
• Если и — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой равен углу между этой касательной и прямой .
• Прямая, проведенная через середины отрезков, отсеченных двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
  • Эквивалентная формулировка: через середины двух любых параллельных хорд эллипса проходит какой-либо диаметр эллипса. В свою очередь, любой диаметр эллипса всегда проходит через центр эллипса.
• Эволютой эллипса является астроида, вытянутая вдоль вертикальной оси.
• Точки пересечения эллипса с осями являются его вершинами.
• Эксцентриситет эллипса, то есть отношение характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
  • Если эксцентриситет эллипса равен нулю (что то же самое, что фокальное расстояние равно нулю: {\displaystyle F_{1}F_{2}=0}), то эллипс вырождается в окружность.
• Экстремальные свойства
  • Если — выпуклая фигура и — вписанный в -угольник максимальной площади, то

    

где обозначает площадь фигуры .

• Более того: равенство достигается в том и только в том случае, если {\displaystyle F} ограничено эллипсом.

• Среди всех выпуклых замкнутых кривых, ограничивающих данную площадь, эллипсы и только они имеет максимальную аффинную длину.

• Если произвольный эллипс вписан в треугольник ABC и имеет фокусы P и Q, тогда для него справедливо соотношение

• Если лестницу (бесконечно тонкий отрезок прямой) прислонить к вертикальной стенке с горизонтальным полом, и один конец лестницы будет скользить по стенке (все время касаясь ее) а второй конец лестницы будет скользить по полу (все время касаясь его), тогда любая фиксированная точка лестницы (не на ее концах), будет двигаться по дуге некоторого эллипса. Это свойство остается верным, если мы возьмем точку не внутри лестницы-отрезка, а на ее мыслимом продолжении. Последнее свойство используется в описанном выше[⇦] эллипсографе.

• Касательная, проходящая через точку , принадлежащую эллипсу, имеет следующее уравнение:

Применение эллипса

с помощью Эллипса сделали революционное открытие в астрономии

В XVI веке математик и астроном древности Кеплер доказал, что каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце

вычисление хода отражения

движенее материальной точки по эллиптической кривой

канонические уравнения эллипса и гиперболы

Тебе нравиться эллипс? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое эллипс, канонические уравнения эллипса и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Линейная алгебра и аналитическая геометрия

Из статьи мы узнали кратко, но содержательно про эллипс